Sejak kami mulai mempelajari matematika di sekolah dasar, mulai belajar menghitung dan menjumlahkan, sedikit banyak kami telah memahami tentang dasar-dasar matematika.
Bagi sebagian orang seolah-olah matematika, baik dari perkalian, pecahan, dan bahkan hingga statistik, memungkinkan mereka untuk lebih mengenali dunia ini, mempelajari matematika sebagai disiplin dan filosofi lebih dari sebatas lulus ujian!
Dari sekolah menengah hingga pendidikan lanjut, matematika menyediakan berbagai konsep yang dipelajari dengan baik dan tak terbantahkan: ada penyelesaian konkret untuk setiap konsep dan soal yang diberikan, penyelesaian yang Anda periksa berulang kali! Mungkin mudah untuk percaya bahwa logika di balik matematika tidak menimbulkan pertanyaan lebih lanjut sehingga tidak diperlukan penelitian lebih lanjut ...
Namun, ada beberapa masalah dalam matematika yang belum pernah terpecahkan hingga saat ini, dan bahkan para ilmuwan dan peneliti terhebat yang pernah ada pun belum dapat menemukan solusinya.
Teka-teki ini berhubungan dengan pemahaman kita tentang beberapa konsep paling mendalam dalam matematika dan mendefinisikan atau mempertanyakan pengetahuan kita tentang fakta-fakta matematika dasar.
Mungkin Anda mengikuti pelajaran matematika hanya untuk lebih berhasil dalam akademis Anda, baik itu lulus ujian atau mendapatkan nilai tugas keterampilan yang bagus. Namun, pernahkah Anda membayangkan bahwa sejatinya Anda ditakdirkan untuk hal yang lebih besar? Anda bisa menjadi orang pertama yang memecahkan salah satu misteri matematika berikut ini!
Menemukan penyelesaian untuk salah satu dari ketujuh permasalahan ini Anda akan mendapatkan hadiah sebesar $ 1 juta atau setara dengan sekitar 14 Triliun rupiah! Tertarik bukan?
SuperProf menampilkan untuk Anda daftar masalah matematika yang belum terpecahkan ini dan kami berharap suatu hari nanti dapat membaca biografi Anda di buku sejarah setelah menyelesaikan satu (atau lebih!) dari masalah tersebut!

Hipotesis Riemann
Hipotesis ini untuk sebagian besar ilmuwan atau alhi matematika sebagai salah satu soal matematika paling susah di dunia. Akibatnya, hipotesis Riemann tidak pernah terpecahkan!
Ini pasti alasan mengapa hari ini begitu sedikit peneliti yang memilih untuk mempelajarinya: karena takut menyia-nyiakan karir mereka pada misteri yang tampaknya tidak mungkin untuk dipecahkan.
David Hielbert membuat hipotesis Riemann terdaftar sebagai nomor 8 dalam daftar masalah yang dipresentasikan di Congress of Parisian Mathematicians pada sekitar tahun 1900. 100 tahun kemudian, Clay Mathematics Institute memasukkannya ke dalam daftar "Masalah milenium".
Memecahkan hipotesis Riemann akan mendapatkan hadiah $ 1 juta!
Mungkinkah ini menjadi alasan terbaik untuk mengambil kursus matematika, jikalau mungkin suatu hari dapat memecahkan masalah yang dikenal sebagai "holy grail of mathematicians"?
Pada tahun 1859, Bernard Riemann menerbitkan artikel berjudul “On the number of primes less than a given quantity”, tanpa menyadari bahwa nyatanya dia baru saja mengajukan pertanyaan paling rumit dalam sejarah matematika.
Hipotesisnya mulai menjawab pertanyaan yang belum dapat dijawab oleh ahli matematika selama 2000 tahun terakhir, yakni tentang bagaimana asal mula bilangan prima.
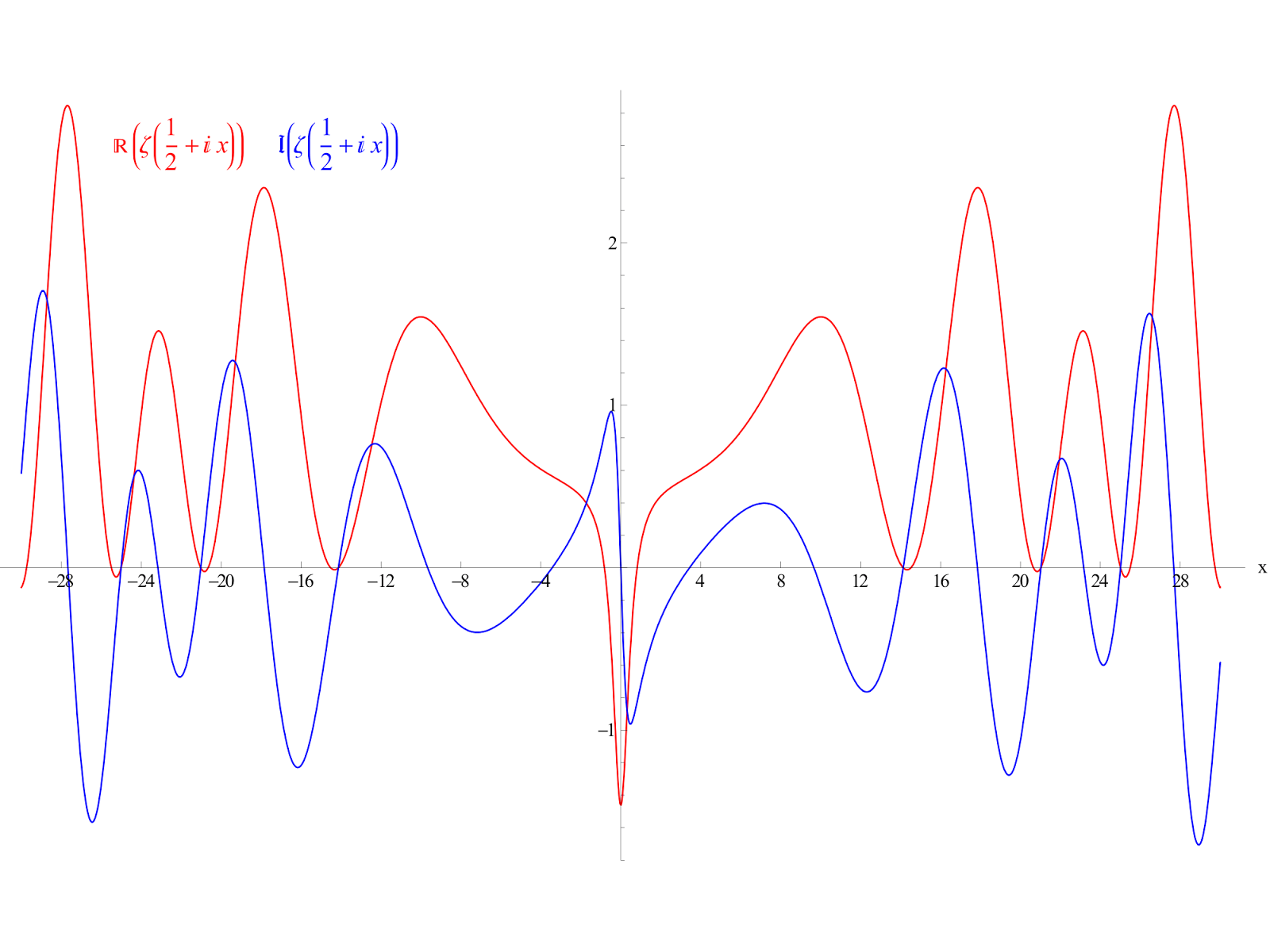
Mengikuti karya profesornya yakni Gauss, Riemann yang berasal dari Jerman memperbarui fungsi Zeta.
Apa artinya ini? Dia membuat grafik 3D dan melihat bahwa fungsinya hanya bernilai nol pada bilangan negatif genap dan bilangan kompleks dengan real ½. Menurutnya, titik nol tersebut memiliki keterkaitan dengan bilangan prima.
Membuktikan fungsi Zeta ini akan membantu Anda menemukan asal mula bilangan prima yang terkenal.
Cek di sini jika ingin mencari guru privat matematika
Konjektur Hodge
Yang juga termasuk dalam daftar tujuh masalah milenium adalah konjektur Hodge: mengabungkan beberapa keterampilan matematika yang sebelumnya tidak pernah dikaitkan, yakni topologi aljabar dengan geometri aljabar.
Menurut definisi ini dari Clay Institute, konjektur mengajukan pertanyaan tentang variasi proyeksi kompleks (yang merupakan jenis ruang topologi tertentu) - Objek Hodge adalah kombinasi linier dengan koefisien rasional dari tingkatan yang meningkat dengan objek geometris aljabar.
Claire Voisin, seorang matematikawan asal Prancis ini, telah mengerjakan hipotesis ini. Menurutnya, bukti akan memberikannya harta matematika yang nyata!
Dalam sebuah wawancara, dia meringkas Konjektur Hodge dengan menjelaskan bahwa jenis objek dari berbagai proyeksi kompleks, adalah kumpulan poin dalam kumpulan yang diproyeksikan dan yang ditentukan oleh batasan polinomial.
Cukup rumit, bukan?
Mungkin ini adalah masalah yang paling sulit untuk dipecahkan, mungkin saja tidak, tetapi yang pasti yang paling sulit untuk dipahami dengan pengetahuan matematika yang mendalam dan pendalaman yang harus Anda miliki dapat membantu memahami teka-teki tersebut!
Memecahkannya adalah sebuah pertanyaan, misalkan tentang bagaimana geometri yang tidak dapat kita visualisasikan membuatnya semakin sulit untuk dipahami!
Mungkin beberapa les online matematika privat dapat membantu Anda mencapainya?
Konjektur Collatz
Konjektur Collatz adalah salah satu soal matematika tersulit di dunia yang sampai saat ini belum terpecahkan, meskipun telah diuji untuk miliaran angka. Konjektur ini, yang juga dikenal sebagai masalah 3n + 1, pertama kali diperkenalkan oleh matematikawan Lothar Collatz pada tahun 1937. Inti dari konjektur ini sangat sederhana: mulailah dengan suatu bilangan bulat positif, dan lakukan dua operasi berikut:
- Jika bilangan tersebut genap, bagi dengan 2.
- Jika bilangan tersebut ganjil, kalikan dengan 3 dan tambahkan 1.
Kemudian, teruskan operasi ini dengan bilangan baru yang dihasilkan. Konjektur Collatz menyatakan bahwa apapun bilangan awal yang Anda pilih, Anda akan selalu mendapatkan angka 1 setelah beberapa langkah.
Namun, meskipun terlihat benar setiap kali diuji, tidak ada bukti matematis yang mengonfirmasi bahwa hal ini berlaku untuk semua bilangan bulat positif. Dengan kata lain, meskipun sudah diuji untuk angka yang sangat besar, belum ada seorang pun yang bisa membuktikan kebenaran konjektur ini secara formal.
Konjektur Birch / Swinnerton-Dyer
Konjektur/dugaan khusus ini adalah pertanyaan tentang persamaan aljabar, salah satu konsep matematika yang mungkin sudah Anda kenali setelah mempelajari Aljabar sejak sekolah menengah!
Akan tetapi, Anda harus memiliki keterampilan tertentu dalam matematika sebelum mencoba memecahkan dugaan khusus ini! Mungkinkah sedikit pengetahuan tentang kalkulus dapat membantu Anda mulai menyelesaikannya?
Dugaan tersebut mencoba untuk menentukan jumlah titik yang berbeda pada kurva elips.
Menentukan solusi untuk persamaan polinomial (di mana x atau y = 0) saja sudah cukup rumit, di mana x dan y adalah bilangan rasional…
Dugaan ini bersama dengan hadiah $ 1 jutanya, memperumit beberapa hal dengan menyarankan bahwa penyelesaian bergantung pada jumlah penyelesaian pada setiap bilangan prima P.
Persamaan Navier-Stokes
Yang ini lebih fokus pada pertanyaan seputar fisika dan dinamika fluida!
Tidak seterkenal Einstein dengan E = MC², persamaan Navier-Stoke telah menarik perhatian fisikawan dan matematikawan dan berkaitan dengan pergerakan fluida.
Cek di sini jika sedang mencari guru matematika SD

Ini terdiri dari persamaan diferensial non-linier, dan uniknya adalah faktabahwa persamaan tersebut sudah sering digunakan, meskipun kami belum menemukan penyelesaiannya!
Antara lain digunakan untuk lebih memahami bagaimana pergerakan arus di lautan.
Jika Anda memiliki keterampilan matematika atau fisika yang hebat, membuktikan soal matematika yang belum terpecahkan ini membuat Anda mendapatkan gelar ke-2 untuk memecahkan salah satu dari tujuh masalah Clay Institute, dan tentunya menjadi seorang milyiader!
Sejauh ini, hanya konjektur Poincaré yang terbukti.
Landau's Problems
Pada Kongres Internasional Matematika 1912, matematikawan Edmund Landau mengemukakan empat masalah dasar tentang bilangan prima yang dikenal sebagai Landau's problems. Dalam pidatonya, Landau menyebutkan bahwa masalah-masalah ini “belum bisa diselesaikan dengan keadaan matematika saat itu.” Hingga 2025, semua rumus matematika tersulit ini tetap belum terpecahkan.
Pertanyaan-pertanyaan matematika sulit yang diajukan Landau berfokus pada sifat dan distribusi bilangan prima, yang merupakan bilangan yang hanya dapat dibagi dengan 1 dan dirinya sendiri.
Beberapa masalah ini melibatkan pencarian pola atau hubungan antara bilangan prima, sementara yang lain berfokus pada pertanyaan yang lebih mendalam mengenai bilangan prima dalam konteks teori bilangan.
Landau juga memperkenalkan masalah distribusi bilangan prima dalam rentang tertentu, yang hingga saat ini masih menjadi tantangan besar dalam dunia matematika.
Konjektur Goldbach

Konjektur Goldbach adalah salah satu masalah mtk tersulit paling dikenal dan terus menerus menjadi tantangan dalam dunia teori bilangan. Diusulkan oleh matematikawan Prusia, Christian Goldbach pada tahun 1742, konjektur ini menyatakan bahwa setiap bilangan genap yang lebih besar dari dua dapat ditulis sebagai jumlah dua bilangan prima. Sebagai contoh:
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 3 + 7
Meskipun konjektur ini telah diuji untuk angka-angka yang sangat besar dan selalu terbukti benar, hingga saat ini tidak ada bukti matematis formal yang dapat memastikan bahwa hal ini berlaku untuk semua bilangan genap.
Hal ini membuat Konjektur Goldbach tetap menjadi salah satu daftar soal matematika yang belum terpecahkan. Meskipun matematikawan modern terus mencari solusi atau bahkan bukti penyangkalan terhadap konjektur ini, hingga saat ini masalah ini masih terus menjadi teka-teki besar dalam dunia matematika.

Teori Yang-Mills
Masalah berbasis fisika lainnya yakni teori Yang Mills yang bertujuan untuk mengatasi permasalahan dalam pemahaman kita tentang kekuatan fundamental alam semesta.
Untuk menjelaskan partikel ini, Yang dan Mills mencoba mendeskripsikan partikel unsur dengan membangun model berdasarkan teori geometris.
Teori mereka yang mengatakan bahwa partikel kuantum tertentu memiliki massa positif telah diverifikasi oleh sejumlah simulasi komputer.
Ditemukannya oleh dua fisikawan hebat, teori tersebut belum dapat dipecahkan hingga saat ini dan masih sebatas sebuah gagasan.
Hilbert's Problems
Pada tahun 1900, matematikawan Jerman David Hilbert mengajukan daftar 23 masalah dalam matematika yang dikenal dengan Hilbert’s Problems. Masalah-masalah matematika yang paling susah ini disampaikan dalam pidatonya di Kongres Matematika Internasional di Paris, dan menjadi salah satu referensi penting dalam perkembangan matematika di abad ke-20.
Hilbert menyebutkan masalah-masalah ini sebagai tantangan besar bagi para matematikawan yang akan datang, dan beberapa di antaranya telah menjadi masalah matematika tersulit yang masih menunggu solusi hingga kini.
Beberapa pertanyaan mtk tersulit di dalam daftar Hilbert telah terpecahkan, seperti masalah pertama yang berkaitan dengan teori bilangan dan masalah kedua yang berhubungan dengan geometri aljabar. Namun, ada beberapa masalah, seperti masalah kedelapan dan masalah keenam, yang masih belum terpecahkan.
Thurston's 24 Questions
Di tahun 1982, seorang matematikawan Amerika bernama William Thurston mengajukan 24 masalah yang dikenal sebagai Thurston’s 24 Questions. Soal matematika tersulit ini berfokus pada geometri diferensial dan topologi geometri.
Masalah-masalah ini muncul dalam makalahnya yang berjudul Three-dimensional manifolds, Kleinian groups and hyperbolic geometry, yang dipublikasikan di Bulletin of the American Mathematical Society.
Thurston’s 24 Questions berfokus pada teori manifold tiga dimensi dan sangat berpengaruh dalam pengembangan topologi geometrik. Masalah-masalah ini berkaitan dengan karakteristik geometri ruang dan hubungan antara ruang hiperbolik dan geometri topologi lainnya.
Seperti banyak soal tersulit di dunia yang belum terpecahkan lainnya, pertanyaan-pertanyaan ini menantang pemahaman kita tentang bentuk ruang tiga dimensi.
Simon Problems
Simon’s problems adalah rangkaian 15 pertanyaan mtk paling susah yang diajukan oleh Barry Simon, seorang matematikawan dan fisikawan asal Amerika pada tahun 2000. Masalah-masalah ini berfokus pada teori operator kuantum dan perilaku spektral operator Schrödinger. Beberapa masalah ini berhubungan dengan teori spektrum dan dinamika kuantum, dengan fokus khusus pada sistem yang mengandung potensi Coulomb.
Pada tahun 2014, matematikawan Artur Avila memenangkan Medali Fields setelah berhasil memecahkan tiga dari masalah Simon, salah satunya adalah membuktikan bahwa set tingkat energi dari sistem kuantum abstrak tertentu adalah set Cantor, yang dikenal dengan nama "Ten Martini Problem".
Meskipun beberapa masalah ini telah mengalami kemajuan, banyak yang masih tetap menjadi tantangan besar dalam dunia fisika matematika dan teori operator.
P = NP
Teka-teki satu ini mungkin yang paling penting dari semuanya.
Pada dasarnya, penyelesaian masalah ini akan menyelesaikan banyak masalah lainnya, sedangkan selama masih belum bisa terselesaikan, maka begitu pula terjadi untuk kebanyakan permasalahan lain di bidang matematika dan komputasi. Banyak penghitungan yang dilakukan saat ini dikenal sebagai masalah NP-hard, karena termasuk dalam kategori ini.

Dalam P = NP, kita menyebut P sebagai masalah, di mana solusinya adalah sekelompok elemen dari himpunan tertentu.
Terkait erat dengan fungsi komputer dan algoritma, dapat disimpulkan masalah ini sebagai pertanyaan berikut:
Bisakah kita menentukan, dengan perhitungan apa yang bisa kita hitung dari keberuntungan?
Bisakah Anda menjawab pertanyaan ini yang belum jua terjawab?
Pelajari cara membuat grafik fungsi di sini.
Bilangan Ramsey
Bilangan Ramsey terkait dengan keteraturan dan model untuk jantung berbagai sistem. Menurut teori ini, ketidakteraturan sejati tidak mungkin adanya.
Dapat diringkas demikian: jika kita menggambar n titik pada selembar kertas, saat titik dihubungkan ke semua titik lain dengan garis merah atau biru, dimana n harus sama dengan 6 untuk memastikan bahwa setidaknya akan ada satu segitiga yang berwarna merah atau biru.
Sederhananya, kita bisa mempertanyakan berapa jumlah kelompok kita karena setidaknya tiga anggotanya adalah orang asing dan tiga orang lainnya memiliki hubungan timbal balik. Jawaban dari soal tersebut adalah 6.
Namun, jika kita mengubah angka 3 dengan 4, masalahnya tidak mungkin dapat diselesaikan. Atau setidaknya, sampai sejauh ini tidak ada ahli matematika yang berhasil memecahkan soal mtk tersulit di dunia ini.
Bisakah Anda menemukan formula yang tepat?
Cek di sini untuk tempat les matematika di Medan
Taniyama's Problems
Pada tahun 1955, Yutaka Taniyama, seorang matematikawan asal Jepang, mengajukan 36 masalah yang dikenal sebagai Taniyama’s Problems, yang berfokus pada geometri aljabar dan teori bilangan.
Masalah-masalah matematika paling sulit ini berkaitan dengan hubungan antara kurva eliptik dan bentuk modular. Salah satu masalah penting dalam rangkaian masalah ini adalah Taniyama-Shimura conjecture, yang menjadi dasar bagi pembuktian Teorema Terakhir Fermat oleh Andrew Wiles pada tahun 1995.
Meskipun masalah-masalah ini telah memberikan dasar bagi banyak penelitian dalam teori bilangan, beberapa dari Taniyama’s Problems masih tetap belum terpecahkan, dan menjadi tantangan besar hingga saat ini.
Smale's Problems
Pada tahun 1998, matematikawan Steve Smale mengajukan daftar 18 masalah yang dikenal dengan nama Smale’s Problems. Masalah-masalah ini diajukan sebagai tantangan untuk abad ke-21, dan berfokus pada analisis matematis dan sistem dinamis.

Beberapa masalah ini berhubungan dengan sistem dinamika nonlinier dan geometri diferensial, dan tantangan utamanya adalah menemukan solusi yang berlaku untuk berbagai sistem matematis yang sangat kompleks.
Masalah-masalah ini membuka jalan bagi pemahaman yang lebih dalam tentang sistem dinamis dan geometri dalam dimensi yang lebih tinggi. Namun, banyak dari Smale’s Problems masih belum terpecahkan, dan tetap menjadi salah satu daftar soal matematika tersusah di dunia yang menunggu untuk dijawab.
Bilangan Lychrel dan Palindrom
Untuk memahami bilangan Lychrel, Anda harus terlebih dahulu mengetahui definisi palindrom.
Palindrom bisa berbentuk angka atau kata yang jika dibaca dari kiri ke kanan maupun kanan ke kiri, bacaannya sama.
17371 adalah contoh nomor palindrom, karena bunyinya sama (memiliki nilai sama), baik Anda mulai dari kiri atau kanan.
Ketika kita berulang kali menambahkan angka dengan kebalikannya dan hasilnya tidak membentuk palindrom, itu disebut dengan bilangan Lychrel.
59 bukanlah tergolong bilangan Lychrel karena…
59 + 95 = 154
154 + 451 = 605
605 + 506 = 1111
Sebenarnya, kami berakhir dengan bilangan palindrom lain.
Angka terkecil yang palindromnya belum kami temukan adalah 196, dan inilah yang menjadi motivasi tersendiri bagi setiap peneliti matematika: belum tahu persis bagaimana memecahkan masalah ini ... belum bukan tidak!
Bahkan setelah lebih dari 12 juta kali penambahan berulang (tentu saja berkat bantuan kalkulator atau alat hitung otomatis lainnya!), kami belum menemukan palindrome untuk bilangan 196!
Untungnya, untuk menjadi ahli matematika, Anda tak perlu menyelesaikan soal matematika di atas. Superprof dapat membantu Anda menemukan guru matematika yang tepat agar Anda menjadi ahli matematika.
Dengan bantuan seorang guru yang berpengalaman, Anda bisa mengasah keterampilan matematika Anda dan siapa tahu, mungkin Anda adalah orang yang akan memecahkan soal matematika rumit ini!
Ringkaskan dengan AI
















