Polinomial adalah salah satu konsep dasar yang sangat penting, terutama dalam aljabar. Konsep ini mencakup berbagai jenis operasi rumus mtk kelas 10, seperti penjumlahan, pengurangan, perkalian, hingga pembagian polinomial. Dalam artikel ini, kita akan membahas secara lengkap mengenai suku banyak, mulai dari pengertian hingga bagaimana menyelesaikan bentuk polinomial dengan berbagai jenis operasi.
Apa Itu Polinomial?
Polinomial atau suku banyak adalah ekspresi matematika yang terdiri dari satu atau lebih suku yang dipisahkan oleh tanda operasi seperti penjumlahan atau pengurangan. Fungsi suku banyak polinomial adalah untuk menggambarkan hubungan antara variabel dan koefisien yang berhubungan dengan pangkat tertentu yang mana ini berhubungan dengan fungsi matematika. Bentuk polinomial yang umum dapat ditulis sebagai berikut:
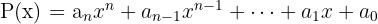
Yang mana:
- P(x) adalah fungsi polinomial.
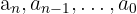adalah koefisien dari setiap suku polinomial.- x adalah variabel yang dapat digantikan dengan nilai suku banyak.
- n adalah derajat atau pangkat tertinggi dari polinomial.
Agar lebih paham dapat dilihat contoh bentuk polinomial berikut:
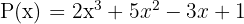
Dalam contoh tersebut, derajat dari polinomial ini adalah 3, karena pangkat tertinggi dari x adalah 3. Setiap suku dalam polinomial ini memiliki koefisien yang berhubungan dengan pangkat x, yakni 2, 5, -3, dan 1. Polinomial bisa memiliki satu variabel atau lebih.
Cek di sini untuk kursus matematika terbaik
Persamaan Polinomial
Persamaan polinomial terjadi ketika dua polinomial memiliki bentuk yang sama dan koefisien-koefisiennya juga identik pada setiap pangkat variabel. Dengan kata lain, dua polinomial dikatakan setara atau sama jika kedua polinomial tersebut menghasilkan hasil yang sama untuk setiap nilai variabel yang disubstitusikan.
Untuk menyatakan kesamaan polinomial, kita menggunakan tanda 
, yang berarti kedua polinomial memiliki kesamaan di semua pangkat variabel. Misalnya:
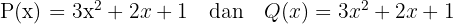
Karena koefisien pada setiap pangkat x di kedua polinomial tersebut identik, maka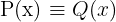 
.
Penjumlahan Polinomial
Penjumlahan polinomial adalah operasi yang dilakukan dengan cara menjumlahkan dua atau lebih polinomial yang memiliki pangkat yang sama pada variabel yang bersesuaian. Proses penjumlahan ini cukup sederhana karena hanya melibatkan penjumlahan koefisien-koefisien dari suku-suku yang memiliki pangkat yang sama. Dengan kata lain, kita hanya perlu menjumlahkan suku-suku yang memiliki pangkat yang identik dan mengabaikan suku-suku yang tidak memiliki pangkat yang sama.
Misalnya, jika ada dua polinomial:
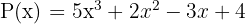dan 
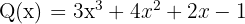
Untuk melakukan penjumlahan polinomial ini, kita akan menjumlahkan suku-suku yang memiliki pangkat yang sama. Jadi, kita akan menjumlahkan koefisien dari suku yang memiliki pangkat 
, 
, x, dan bilangan konstan:
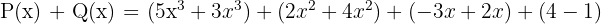
Hasil penjumlahan polinomial ini adalah:
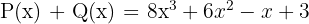
Dengan demikian, hasil penjumlahan polinomial P(x) dan Q(x) adalah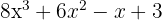 
.
Penting untuk diingat bahwa penjumlahan polinomial hanya dapat dilakukan pada suku yang memiliki pangkat yang sama. Suku yang tidak memiliki pangkat yang sama tidak dapat dijumlahkan, sehingga perlu dikelompokkan berdasarkan pangkatnya terlebih dahulu.
Pengurangan Polinomial
Pengurangan polinomial dilakukan dengan cara yang hampir sama dengan penjumlahan polinomial, namun di sini kita mengurangi koefisien dari suku yang memiliki pangkat yang sama. Proses pengurangan polinomial ini memerlukan perhatian pada tanda negatif, karena kita harus mengurangi koefisien-koefisien yang ada sesuai dengan tanda yang ada di dalam polinomial.
Misalnya, kita ingin mengurangi dua polinomial berikut:
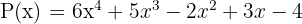dan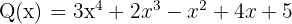 
Untuk mengurangi polinomial P(x) dengan Q(x), kita akan mengurangkan koefisien-koefisien dari suku yang memiliki pangkat yang sama. Jadi, kita akan melakukan pengurangan pada suku 
, , , x, dan konstanta:
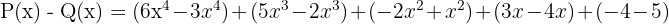
Hasil pengurangannya adalah:
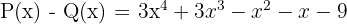
Jadi, hasil pengurangan polinomial P(x) dan Q(x) adalah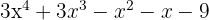 
. Dalam hal ini, kita melihat bahwa pengurangan polinomial juga melibatkan penyesuaian tanda koefisien agar hasilnya tepat.
Seperti pada penjumlahan, pengurangan polinomial juga hanya dilakukan pada suku yang memiliki pangkat yang sama. Hal ini menunjukkan bahwa pengurangan polinomial memerlukan pengelompokan suku berdasarkan pangkatnya terlebih dahulu.
Perkalian Polinomial
Perkalian polinomial suku banyak adalah operasi yang lebih kompleks daripada penjumlahan dan pengurangan. Pada perkalian polinomial, setiap suku dari satu polinomial dikalikan dengan setiap suku dari polinomial lainnya. Hasil dari perkalian ini adalah penjumlahan dari semua hasil perkalian suku-suku tersebut.
Misalnya, kita ingin mengalikan polinomial berikut:
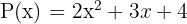dan 
Untuk melakukan perkalian, kita akan mengalikan setiap suku di P(x) dengan setiap suku di Q(x):
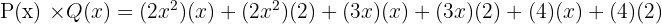
Hasilnya adalah:
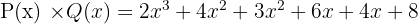
Kemudian kita gabungkan suku-suku yang sejenis:
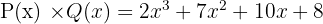
Jadi, hasil perkalian polinomial P(x) dan Q(x) adalah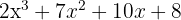 
.
Tambah pengetahuan Matematika Anda dengan memahami limit fungsi dari Aljabar!
Pembagian Polinomial
Pembagian polinomial adalah salah satu konsep penting yang sering digunakan dalam aljabar. Sama seperti pembagian bilangan biasa, pembagian polinomial juga memiliki metode khusus yang bisa digunakan untuk menyelesaikannya. Ada beberapa rumus polinomial yang digunakan untuk menyelesaikan pembagian suku banyak, yaitu sebagai berikut:
Pembagian Bersusun
Pembagian bersusun adalah metode klasik yang digunakan untuk membagi polinomial, mirip dengan cara kita membagi bilangan secara panjang. Berikut adalah langkah-langkahnya:
- Susun polinomial dalam bentuk pembagian panjang.
- Bagilah suku pertama dari polinomial dengan suku pertama dari pembaginya.
- Kalikan hasil bagi dengan pembagi dan kurangkan hasilnya dari polinomial utama.
- Turunkan suku berikutnya dan ulangi prosesnya sampai semua suku habis dibagi atau tersisa sisa pembagian.
Hasil akhir adalah hasil bagi dan jika ada nilai tersisa, itu disebut sisa pembagian.
Metode Horner
Metode Horner adalah metode yang lebih efisien untuk mencari nilai polinomial, terutama untuk polinomial dengan derajat tinggi. Metode ini menggunakan pendekatan berulang untuk menyederhanakan perhitungan.
Langkah-langkah Metode Horner Polinomial
- Tuliskan Setiap Koefisien Polinomial dalam Urutan Menurun:
Mulai dari koefisien suku dengan pangkat tertinggi hingga terendah.
- Tuliskan Nilai Substitusi di Sebelah Kiri:
Misalkan kita ingin mencari nilai polinomial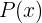 
pada 
.
- Lakukan Operasi Berulang dengan Mengalikan dan Menjumlahkan Koefisien secara Bertahap:
- Tuliskan koefisien pertama di baris pertama.
- Kalikan koefisien pertama dengan nilai substitusi dan tuliskan hasilnya di bawah koefisien kedua.
- Jumlahkan hasil tersebut dengan koefisien kedua dan tuliskan hasilnya di baris ketiga.
- Ulangi langkah ini hingga semua koefisien telah dihitung.
Contoh Soal Metode Horner
Soal 2: Tentukan nilai dari polinomial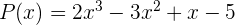 
untuk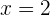 
menggunakan metode Horner.
Penyelesaian:
- Tuliskan setiap koefisien:
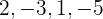. - Tuliskan nilai substitusi 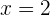di sebelah kiri.
- Lakukan operasi:
- Tuliskan
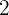(koefisien pertama) di baris ketiga. - Kalikan 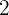(koefisien pertama) dengan 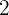(nilai substitusi) dan tuliskan hasilnya
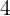di baris kedua. - Jumlahkan
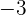(koefisien kedua) dengan 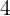untuk mendapatkan 
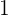. Tuliskan 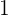di baris ketiga. - Kalikan 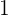dengan 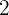untuk mendapatkan 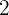. Tuliskan 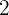di baris kedua.
- Jumlahkan 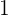(koefisien ketiga) dengan 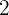untuk mendapatkan
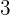. Tuliskan 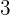di baris ketiga. - Kalikan 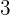dengan 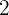untuk mendapatkan
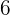. Tuliskan 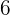di baris kedua. - Jumlahkan
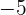(koefisien keempat) dengan 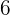untuk mendapatkan 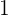. Tuliskan 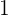di baris ketiga.
- Hasil akhirnya adalah .
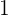Berikut adalah representasi tabel Horner untuk polinomial tersebut:
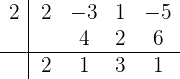
Jadi, nilai polinomial 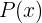untuk 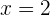adalah 1.
Periksa di sini untuk les matematika Jogja
Teorema Sisa Polinomial
Teorema Sisa Polinomial adalah konsep penting dalam teori aljabar yang digunakan untuk menentukan sisa dari pembagian polinomial tanpa melakukan pembagian panjang yang rumit. Teorema ini menyatakan bahwa jika kita membagi suatu polinomial f(x) dengan divisor x - k, maka sisa dari pembagian tersebut adalah f(k).
Dalam kata lain, kita dapat menentukan sisa dari pembagian suatu polinomial dengan menggantikan nilai x dalam polinomial tersebut dengan nilai k yang ada pada divisor. Sebagai contoh rumus teorema sisa, jika suku banyak:
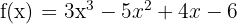
Dan kita ingin membaginya dengan x - 2. Dengan menggunakan Teorema Sisa, kita tinggal mengganti x dengan 2 pada f(x):
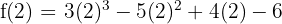
Sekarang kita hitung:
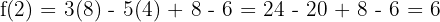
Jadi, sisa pembagian f(x) dengan x - 2 adalah 6. Ini artinya, jika kita melakukan pembagian polinomial f(x) dengan x - 2, sisanya adalah 6.
Teorema Faktor
Teorema Faktor merupakan konsep dasar dalam teori aljabar yang berkaitan erat dengan Teorema Sisa. Teorema ini menyatakan bahwa jika suatu polinomial f(x) habis dibagi oleh faktor (x - k) atau jika f(k) = 0, maka (x - k) adalah faktor dari f(x). Dengan kata lain, jika kita tahu bahwa x = k adalah akar dari polinomial f(x), maka kita dapat mengatakan bahwa (x - k) adalah faktor dari f(x). Jadi jika kita memiliki bentuk polinomial:
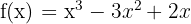
Kita ingin mengetahui faktor-faktor dari f(x). Langkah pertama adalah mencari akar dari polinomial tersebut. Kita coba substitusi nilai x = 0:
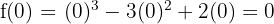
Karena f(0) = 0, ini berarti x = 0 adalah akar dari f(x), dan oleh karena itu, (x - 0) atau x adalah faktor dari f(x).
Sekarang, kita bagi f(x) dengan x menggunakan pembagian polinomial untuk mendapatkan faktor lainnya:
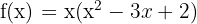
Kita sekarang dapat memfaktorkan polinomial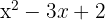 
:
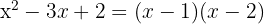
Jadi, faktor lengkap dari f(x) adalah:
Kamu juga perlu tahu tentang pengertian bilangan rasional, pelajari di sini!
Contoh Soal Polinomial
Berikut ini adalah beberapa contoh soal polinomial beserta pembahasannya agar anda semakin paham mengenai materi polinomial:
1. Tentukan hasil penjumlahan P(x) + Q(x), Jika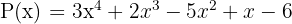 
dan 
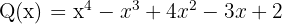
Pembahasan:
Untuk menjumlahkan polinomial P(x) dan Q(x), kita cukup menjumlahkan koefisien dari suku-suku yang memiliki pangkat yang sama.
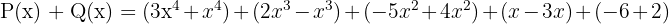
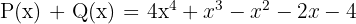
Jadi, hasil penjumlahan polinomial P(x) dan Q(x) adalah:
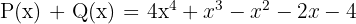
2. Tentukan hasil dari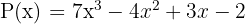 
dikurangi dengan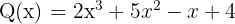 
Pembahasan:
Untuk melakukan pengurangan polinomial P(x) dan Q(x), kita akan mengurangkan koefisien dari suku-suku yang memiliki pangkat yang sama.
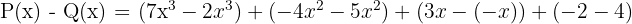
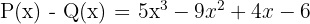
Jadi, hasil pengurangan polinomial P(x) dan Q(x) adalah:
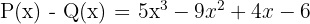
3. Tentukan hasil dari 
, jika 
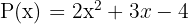dan
Pembahasan:
Untuk mengalikan P(x) dengan Q(x), kita mengalikan setiap suku dari P(x) dengan setiap suku dari Q(x):
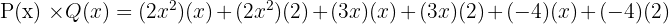
Hasilnya:
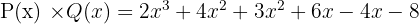
Kemudian kita gabungkan suku-suku yang sejenis:
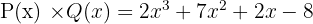
Jadi, hasil perkalian polinomial P(x) dan Q(x) adalah:
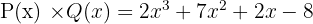
4. Tentukan sisa pembagian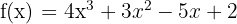 
dengan x - 1
Pembahasan:
Menurut rumus sisa polinomial, untuk mengetahui sisa pembagian polinomial f(x) dengan x - 1, kita hanya perlu menggantikan x dengan 1 pada f(x).
Substitusi x = 1 ke dalam f(x):
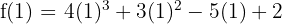
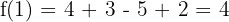
Jadi, sisa pembagian f(x) dengan x - 1 adalah 4.
5. Selesaikan Pembagian polinomial Berikut: (x³ - 6x² + 11x - 6) ÷ (x - 2)
Pembahasan:
Untuk menyelesaikan pembagian ini, kita dapat menggunakan cara horner polinomial.
Metode Horner lebih cepat digunakan jika pembaginya berbentuk x - k. Untuk pembagian ini, kita menggunakan x - 2, sehingga k = 2.
| Koefisien | 1 | -6 | 11 | -6 |
| 2 (pembagi) | 2 | -8 | 6 | |
| Hasil | 1 | -4 | 3 | 0 (sisa) |
Jadi hasil bagi dari kedua polinomial diatas adalah:
x2−4x+3x² - 4x + 3 dan sisa pembagian: 0
Karena sisa = 0, maka (x - 2) adalah faktor dari polinomial tersebut.
Pahami juga rumus-rumus integral dalam Matematika di artikel Kami lainnya!
Apakah sekarang kamu sudah paham tentang konsep dasar suku banyak? Ternyata, mempelajari matematika bukanlah perkara yang sulit jika kita mulai dari konsep dasar dan rajin berlatih. Jika kamu masih merasa kesulitan, jangan ragu untuk bergabung bersama Superprof.
Di Superprof, kamu bisa memilih les privat bersama guru matematika berpengalaman yang siap membantumu memahami konsep-konsep sulit dengan cara yang lebih mudah dipahami. Coba les privat matematika untuk mendapatkan bimbingan yang lebih personal. Kamu bisa memilih belajar online atau tatap muka, sesuai dengan kebutuhanmu. Segera daftar dan mulailah perjalananmu untuk menguasai matematika dengan lebih mudah bersama kami sekarang!
Jika Kamu tertarik dengan baris dan deret aritmatika, Kami sarankan untuk mempelajarinya bersama Superprof!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
Link nya mana
Link apa ya kak