Bagi Anda yang sedang duduk di bangku kelas 10, Anda mungkin sudah atau akan segera familier dengan materi trigonometri. Untuk mengingat kembali, trigonometri adalah sebuah cabang matematika yang membahas mengenai relasi antara sudut dan sisi pada segitiga. Kalau diartikan secara harfiah, trigonometri berasal dari bahasa Yunani, yaitu trigonon yang artinya tiga sudut, dan metron yang berarti mengukur.
Selain itu, trigonometri juga identik dengan istilah-istilah seperti sinus (sin), cosinus (cos), tangen (tan), cosecan (cosec), secan (sec), dan cotangen (cot). Agar Anda semakin paham dengan materi trigonometri kelas 10, pada artikel ini, kami akan membahas mulai dari perbandingan trigonometri segitiga siku-siku, sudut sudut istimewa, perbandingan sudut dan sudut relasi, identitas trigonometri, hingga contoh soal dan pembahasannya. Yuk, langsung simak penjelasan selengkapnya berikut!

Rumus Sin Cos
Fungsi trigonometri dasar mencakup sinus (sin) dan kosinus (cos) atau cos dan sin, yang berhubungan dengan besar sudut serta perbandingan sisi-sisi dalam segitiga siku-siku. Sinus suatu sudut didefinisikan sebagai perbandingan sisi yang berhadapan dengan sudut tersebut terhadap sisi miring, sedangkan kosinus merupakan perbandingan sisi yang berdekatan dengan sudut terhadap sisi miring. Kedua fungsi ini menjadi bagian dari identitas dasar trigonometri yang awalnya berlaku untuk sudut lancip.
Rasio ini kemudian diperluas untuk seluruh sudut dalam ukuran radian dan dikenal sebagai fungsi trigonometri. Nilai sin positif pada kuadran I dan II, sedangkan cos bernilai positif pada kuadran I dan IV. Adapun jangkauan (range) fungsi sinus maupun kosinus berada pada interval [-1, 1] dengan domain bilangan riil.
Dengan memahami sin rumus, siswa dapat lebih mudah menghitung nilai fungsi sinus pada berbagai sudut, menerapkan identitas trigonometri, serta menyelesaikan soal trigonometri yang melibatkan sudut majemuk atau perbandingan sisi.
Selain itu, hubungan sin dan cos sangat fundamental. Memahami bagaimana sin dan cos saling terkait membantu siswa menyederhanakan persamaan trigonometri dan menghitung nilai fungsi trigonometri lainnya dengan lebih mudah. Contohnya, tangen dapat dihitung dari sin/cos, sedangkan cotangen diperoleh dari cos/sin.
Apa Rumus Sin Cos?
Apabila (x,y) merupakan suatu titik pada lingkaran satuan, dan garis dari titik pusat (0,0) menuju titik tersebut membentuk sudut θ terhadap sumbu x positif, maka koordinat x dan y akan memenuhi teorema Pythagoras, yaitu x2+y2 = 1. Dalam hal ini, nilai x dan y merepresentasikan panjang sisi-sisi segitiga siku-siku. Dari konsep tersebut diperoleh identitas trigonometri dasar, yakni cos2θ+sin2θ = 1. Dalam trigonometri, sin adalah perbandingan antara sisi yang berhadapan dengan sudut tertentu terhadap sisi miring segitiga siku-siku. Konsep ini menjadi dasar untuk memahami identitas trigonometri serta menghitung sudut-sudut majemuk.
Perbandingan Trigonometri pada Segitiga Siku-Siku
Cari tampat les matematika di Medan.
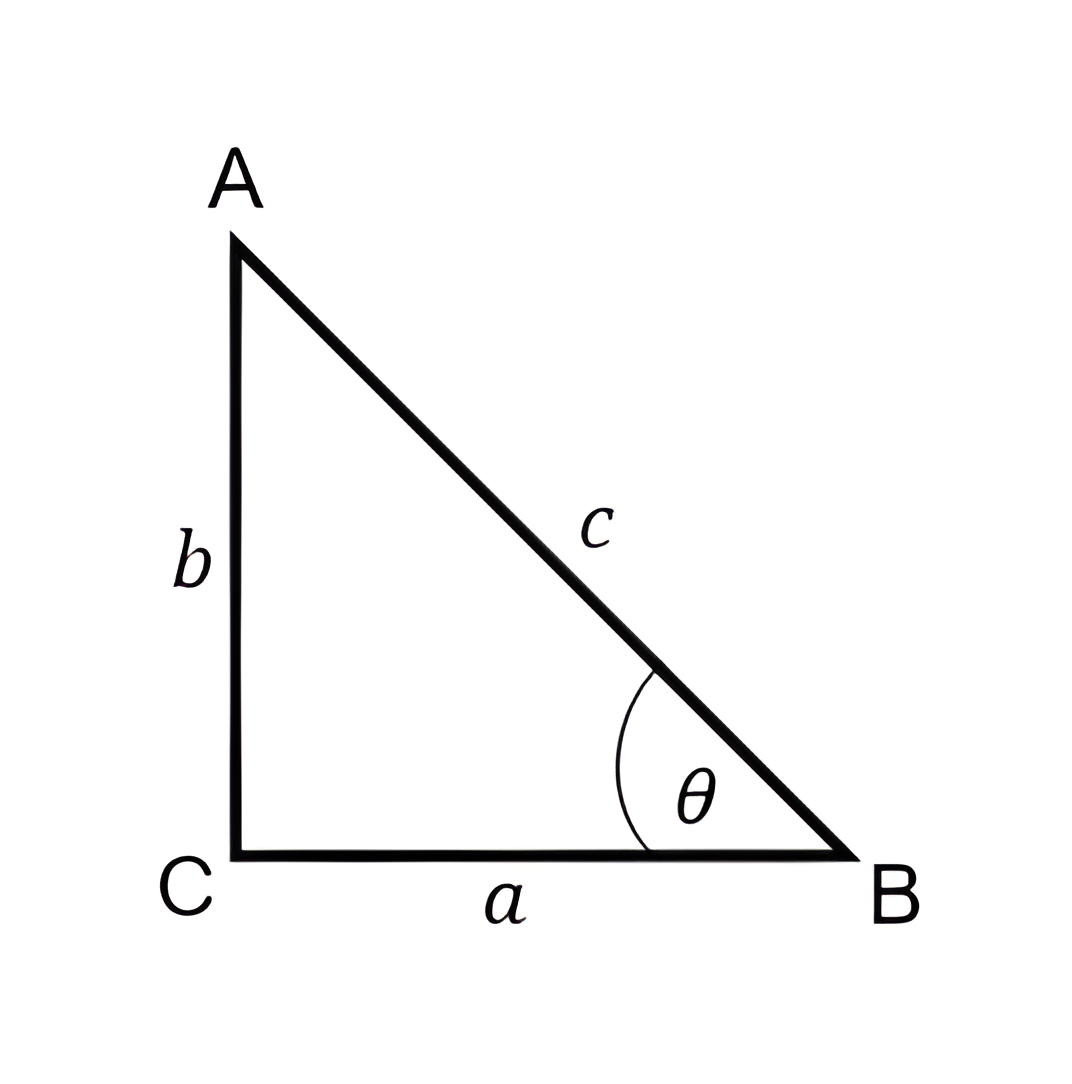
Menurut letak sudutnya, sisi-sisi pada segitiga siku-siku dibagi menjadi 3, sisi depan sudut (sisi b), sisi samping sudut (sisi a), dan sisi miring (sisi c atau hipotenusa) yang berada di depan sudut siku-siku segitiga.
Di sini Anda akan mengenal istilah-istilah matematika seperti sinus (sin), cosinus (cos), tangen (tan), cosecan (csc), secan (sec) dan cotangen (cot), dengan sinus merupakan kebalikan dari cosecan, cosinus adalah kebalikan dari secan, dan tangent adalah kebalikan dari cotangent.
Definisi perbandingan trigonometri pada segitiga siku-siku adalah sebagai berikut:
Sinus θ = sin θ = (sisi depan)/(sisi miring) = b/c
Cosinus θ = cos θ = (sisi samping)/(sisi miring) = a/c
Tangen θ=tan θ= (sisi depan)/(sisi samping) = b/a
Tangen suatu sudut juga dapat ditulis sebagai sin/cos = (sin/cos sama dengan) perbandingan antara sisi depan dan sisi samping. Mengetahui bahwa sin/cos = tan θ membantu siswa menghitung nilai tangen dengan cepat, tanpa harus mengukur sisi segitiga secara langsung.
Berdasarkan definisi perbandingan trigonometri di atas, didapatkan hasil penjabarannya yaitu:
Secan θ = sec θ = 1/cosθ = (sisi miring)/(sisi samping) = c/a
Cosecan θ = csc θ = 1/sinθ = (sisi miring)/(sisi depan) = c/b
Cotangen θ = cot θ = 1/tanθ = (sisi samping)/(sisi depan) = a/b
Selain memahami definisi perbandingan trigonometri di atas, penting juga untuk menguasai rumus sin θ (sinus theta). Rumus ini menyatakan bahwa nilai sinus suatu sudut θ merupakan hasil pembagian antara sisi depan sudut dengan sisi miring atau hipotenusa pada segitiga siku-siku. Secara matematis dituliskan:
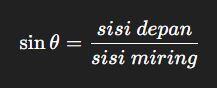
Rumus sinus theta
Konsep rumus sin theta menjadi dasar bagi fungsi trigonometri lainnya, seperti cosinus dan tangen. Rumus ini juga sering muncul dalam soal-soal trigonometri kelas 10, baik dalam bentuk sederhana maupun soal cerita yang menghubungkan panjang sisi segitiga dengan besar sudutnya.
Jika Anda juga ingin belajar tentang rumus barisan dan deret geometri, silahkan pelajari artikel ini!
Sudut Istimewa Trigonometri

Mengetahui sudut-sudut segitiga dengan pasti tidaklah mudah, namun ada beberapa segitiga yang istimewa. Disebut istimewa karena angka-angkanya sangat tepat. Itulah mengapa ada perbandingan trigonometri sudut istimewa.
Sudut-sudut istimewa dalam trigonometri adalah sudut 0˚, 30˚, 45˚, 60˚, 90˚, dan seterusnya, misalnya segitiga sama sisi dan persegi. Segitiga sama sisi memiliki jumlah sudut yang sudah diketahui yaitu 180 derajat, sementara pada persegi, masing-masing sudutnya adalah 90 derajat.
Jika dihitung, maka tabel perbandingan trigonometri sudut istimewa adalah sebagai berikut.
| 0˚ | 30˚ | 45˚ | 60˚ | 90˚ | |
|---|---|---|---|---|---|
| Sin θ | 0 | 1/2 | (1/2) √2 | (1/2) √3 | 1 |
| cos θ | 1 | (1/2) √3 | (1/2) √2 | 1/2 | 0 |
| tan θ | 0 | (1/3) √3 | 1 | √3 | - |
| cot θ | - | √3 | 1 | (1/3) √3 | 0 |
| sec θ | 1 | (2/3) √2 | √2 | 2 | ∞ |
| csc θ | ∞ | 2 | √2 | (2/3) √2 | 1 |
Anda bisa mereservasi guru privat untuk les olimpiade matematika sekarang!

Perbandingan Sudut dan Sudut Relasi Trigonometri

Perbandingan trigonometri sudut berelasi merupakan perluasan dari nilai trigonometri dasar tentang kesebangunan pada sudut segitiga siku-siku, karena sudut siku-siku hanya memenuhi sudut kuadran 1 dan sudut lancip (0˚-90˚) sementara sudut pusat lingkaran adalah 0˚-360˚ yang dibagi menjadi 4 kuadran. Saat mempelajari perbandingan sudut, penting untuk menyadari bahwa fungsi tangen dapat diturunkan dari sin/cos. Konsep ini mempermudah pemahaman identitas trigonometri yang lebih kompleks.
Yang dimaksud kuadran adalah setiap dari empat bagian suatu bidang datar yang terbagi oleh suatu sumbu silang. Sumbu silang tersebut adalah sumbu x dan sumbu y. Jika nilai y positif, maka nilai sin akan positif. Jika sumbu x positif, nilai cos akan positif. Nilai tan akan positif jika x dan y sama-sama positif atau negatif. Terakhir, nilai k akan selalu positif.

Relasi sudut-sudut dalam trigonometri dapat dinyatakan dalam bentuk berikut:
- Pada kuadran I
sin θ = sin θ
cos θ = cos θ
tan θ = tan θ
- Pada kuadran II
sin (180 – θ) = sin θ
cos (180 – θ) = -cos θ
tan (180 – θ) = -tan θ
- Pada kuadran III
sin (180 + θ) = -sin θ
cos (180 + θ) = -cos θ
tan (180 + θ) = tan θ
- Pada kuadran IV
sin (360 – θ) = -sin θ
cos (360 – θ) = -cos θ
tan (360 – θ) = -tan θ
Identitas Trigonometri

Identitas trigonometri adalah kesamaan yang memuat perbandingan trigonometri dari suatu sudut. Identitas trigonometri menyatakan hubungan dari suatu fungsi trigonometri dengan fungsi trigonometri lainnya. Anda akan lebih mudah memahaminya jika sudah paham konsep dasar trigonometri dan pythagoras.
Ada tiga cara untuk menunjukkan kebenaran sebuah identitas trigonometri. Pertama, dengan menyederhanakan ruas kiri menggunakan identitas sebelumnya sampai menjadi bentuk yang sama dengan ruas kanan. Cara kedua, dengan mengubah dan menyederhanakan ruas kanan sampai menjadi bentuk yang sama dengan ruas kiri. Ketiga, mengubah baik ruas kiri maupun ruas kanan ke dalam bentuk yang sama.
Berikut adalah beberapa rumus identitas trigonometri yang perlu Anda ketahui.
- tan θ = sinθ/cosθ
- cot θ = cosθ/sinθ = 1/tanθ
- sec θ = 1/cosθ
- csc θ = 1/sinθ
- sin²x + cos²x = 1
- sin²x = 1 - cos²x
- cos²x = 1 - sin²x
- sec²θ = tan²θ + 1
- csc²θ = cot²θ + 1
Selain itu, untuk sudut-sudut istimewa, penting diketahui bahwa sin 0 adalah 0, sehingga dapat langsung diterapkan dalam penyederhanaan persamaan trigonometri maupun perhitungan nilai fungsi pada sudut lain. Dalam konteks ini, fungsi cotangen juga bisa dijelaskan melalui perbandingan cos/sin, yang secara alami menunjukkan hubungan antara fungsi trigonometri dasar. Memahami konsep cos/sin akan memudahkan siswa menyelesaikan soal-soal yang melibatkan identitas trigonometri tanpa harus menghitung sisi segitiga secara langsung.
Dalam trigonometri, cos/sin adalah perbandingan yang digunakan untuk menghitung cotangen suatu sudut. Konsep ini sangat penting karena cotangen sering muncul dalam soal trigonometri yang melibatkan hubungan antara sisi segitiga. Dengan memahami bahwa cos/sin adalah cara cepat menentukan nilai cot θ, siswa dapat mengerjakan soal dengan lebih efisien tanpa harus menghitung sisi segitiga secara manual.
Selain itu, mengetahui bahwa cos/sin adalah dasar dari cotangen membantu siswa mengaitkan fungsi trigonometri lainnya, seperti tangen yang merupakan kebalikan dari cotangen (sin/cos). Pemahaman ini memudahkan dalam menyederhanakan identitas trigonometri dan menghitung nilai fungsi pada sudut-sudut istimewa atau sudut majemuk.
Apakah rumus tersebut serupa dengan rumus determinan matriks?
Rumus Penjumlahan dan Selisih Sudut (Sinus dan Kosinus)
Sudut yang diperoleh dari hasil penjumlahan maupun pengurangan dua sudut disebut sebagai sudut majemuk. Misalkan sudut tersebut dinyatakan dengan α dan β. Terdapat sejumlah identitas trigonometri yang melibatkan sinus dan kosinus sudut majemuk, yang berguna untuk menyederhanakan maupun menguraikan suatu persamaan trigonometri.
sin(α+β) = sin α cos β + cos α sin β
sin(α−β) = sin α cos β – cos α sin β
cos(α+β) = cos α cos β – sin α sin β
cos(α−β) = cos α cos β + sin α sin β
Perhitungan sudut majemuk sering menggunakan notasi α dan β. Misalnya, sin beta digunakan dalam rumus penjumlahan sudut: sin(α + β) = sin α cos β + cos α sin β, di mana konsep sin kali cos digunakan untuk menentukan nilai fungsi sinus pada sudut gabungan.. Memahami konsep sin beta memudahkan siswa menghitung nilai fungsi sinus pada sudut majemuk tanpa harus menggambar segitiga secara manual.
Selain itu, penerapan sin beta dalam soal trigonometri juga membantu siswa memahami hubungan antar fungsi trigonometri dasar, seperti cos dan tan, serta mempermudah penyederhanaan identitas trigonometri.
Operasi antara fungsi dasar sering muncul dalam trigonometri, salah satunya adalah sin + cos. Memahami sin + cos sangat penting karena kombinasi ini sering digunakan dalam penyederhanaan persamaan trigonometri dan soal yang melibatkan sudut majemuk.
Selain itu, konsep sin + cos membantu siswa melihat hubungan antar fungsi sinus dan kosinus secara bersamaan, sehingga mempermudah perhitungan nilai fungsi pada sudut istimewa maupun kuadran tertentu. Jika Anda ingin belajar fleksibel dari rumah, Anda bisa mempertimbangkan les online matematika untuk memperdalam materi trigonometri dan latihan soal.
Contoh Soal dan Pembahasan
Setelah memahami konsep dan rumus trigonometri, mari kita lihat penerapannya dalam soal matematika. Perhatikan contoh beserta pembahasannya berikut.
- Nilai dari sin 2/3 π + sin 7/3 π adalah..
Jawab:
sin 2/3 π + sin 7/3 π = sin 120˚ + sin 420˚
= sin (1/2) √3 + (1/2) √3 = √3
Jadi, nilai dari sin 2/3 π + sin 7/3 π adalah √3..
- Tentukanlah nilai dari sin 120˚ + cos 201˚ + cos 315˚!
Jawab:
sin 120˚ berada pada kuadran 2, sehingga nilainya tetap positif dengan besar sama seperti sin 120˚ = sin (180-60˚) = sin 60˚ = (1/2) √3
cos 201˚ berada pada kuadran 3, sehingga nilainya negatif dengan besar sama seperti cos 201˚ = cos (180+30˚) = -cos 30˚ = (-1/2) √3
cos 315˚ berada pada kuadran 4, sehingga nilainya positif dengan besar sama seperti cos 315˚ = cos (360-45˚) = cos 45˚ = (1/2) √2
sin 120˚ + cos 201˚ + cos 315˚ = (1/2) √3 - (1/2) √3 + (1/2) √2 = 1/2 √2
Jadi, nilai dari sin 120˚ + cos 201˚ + cos 315˚ adalah (1/2) √2.
Kesimpulan
Materi trigonometri kelas 10 mencakup berbagai konsep dasar yang penting untuk dipahami, mulai dari perbandingan sisi dalam segitiga siku-siku hingga identitas dan rumus penjumlahan atau selisih sudut. Siswa sebaiknya mengingat bahwa sin sama dengan perbandingan sisi depan dengan sisi miring, sementara fungsi lainnya dapat dihubungkan, misalnya cos ke sin, untuk mempermudah penyederhanaan perhitungan.
Selain itu, penting untuk menguasai rumus mencari sin, agar bisa menghitung nilai fungsi sinus dari berbagai sudut, termasuk sudut istimewa maupun sudut majemuk. Dengan memahami rumus sin alpha, siswa dapat menyelesaikan soal trigonometri dengan lebih cepat dan tepat, serta mengaitkan fungsi sinus dengan fungsi trigonometri lainnya seperti cos sin, tan, dan cot.
Secara keseluruhan, pemahaman konsep dasar ini akan memudahkan siswa dalam menerapkan trigonometri di berbagai soal matematika, termasuk identitas trigonometri dan perhitungan sudut gabungan, sehingga belajar trigonometri menjadi lebih menyenangkan dan efektif
Nah, itulah beberapa penjelasan tentang materi trigonometri kelas 10. Jika Anda ingin memperdalam materi ini, Anda bisa menghubungi guru-guru matematika berpengalaman di situs Superprof untuk les matematika privat secara online maupun tatap muka, termasuk mencari tempat les matematika di jakarta timur. Anda juga bisa memeriksa artikel-artikel kami lainnya tentang logika matematika di website Superprof. Selamat belajar!
Ringkaskan dengan AI















help aku punya pr binggung bgtt
halo, silakan pilih guru-guru kami yang sekiranya bisa ngebantu kamu :)