Jika berbicara tentang matematika, maka angka adalah sesuatu yang akan selalu ada dalam pembahasan mengenai matematika. Angka atau bilangan bagaikan nyawa dalam matematika, sebab dengan angka kita bisa mengetahui proses dan hasil mutlak di matematika. Di dalam matematika, angka dapat terbagi berbagai macam sesuai dengan faktornya. Ada angka atau bilangan ganjil, bilangan genap, bilangan bulat, dan bilangan prima.

Apa Itu Bilangan Prima?

Pada pembahasan kali ini kita akan mengulik mengenai bilangan prima atau angka prima. Bilangan prima adalah sebuah bilangan atau angka asli lebih dari 1 yang hanya memiliki dua faktor, yaitu 1 dan angka atau bilangan itu sendiri. Sebuah bilangan prima hanya bisa dibagi dengan angka 1 atau dengan angka itu sendiri. Hal ini juga sering disebut sifat dari bilangan prima.
Misalnya dari angka 1 hingga 10, angka apa saja yang termaksud bilangan prima? Jawabannya adalah 2, 3, 5, dan 7. Empat angka tersebut dikatakan bilangan prima karena ia hanya bisa dibagi dengan angka itu sendiri atau dengan angka 1. Sehingga angka tersebut hanya memiliki dua faktor.
Angka 1 sendiri bukanlah bilangan prima karena angka 1 hanya memiliki satu faktor, sedangkan syarat menjadi bilangan prima adalah memiliki dua faktor, tidak kurang dan tidak lebih dari itu. Sedangkan angka 2 adalah satu-satunya angka genap yang masuk ke dalam bilangan prima sebab ia hanya mempunyai dua faktor yaitu angka 1 dan 2.
Semua angka atau bilangan genap bukanlah angka prima (kecuali angka 2), sebab angka genap bisa dibagi dua dan membuat angka genap memiliki faktor lebih dari dua yaitu angka 1, angka 2, angka itu sendiri, serta angka yang bisa membaginya hingga habis.
Cek di sini jika ingin mengetahui lebih lanjut pengertian kubus
Cara Menghitung Bilangan Prima 1-100
Setelah mengetahui pengertian dan sifat bilangan prima, maka mari kita mencoba menghitung ada berapa bilangan prima 1 sampai 100. Apa saja bilangan prima yang ada di angak 1 sampai 100?
Pertama-tama mari kita buat 10 kolom mendatar dan 10 kolom menurun lalu isi dengan angka 1-100 seperti berikut :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Setelahnya Anda bisa memberikan tanda atau warni kolom pada bilangan yang berkelipatan 2, lanjutkan dengan bilangan kelipatan 3, 5, 7, 11, dan seterusnya. Jika sudah, maka kolom yang tidak berwarna adalah bilangan prima. Seperti hasil berikut :
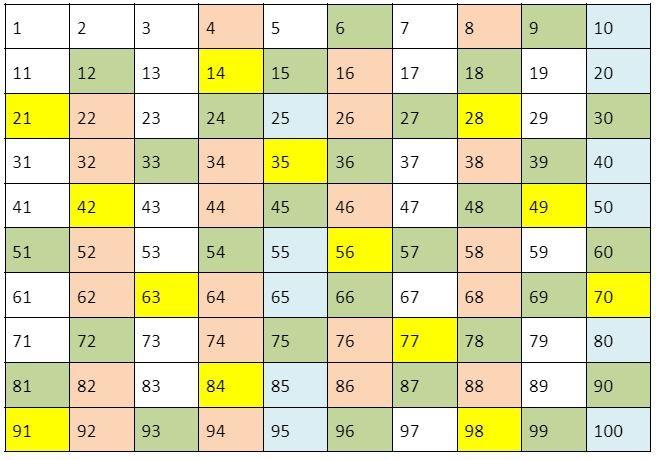
Keterangan :
Merah muda untuk kelipatan 2
Hijau untuk kelipatan 3
Biru untuk kelipatan 5
Kuning untuk kelipatan 7
Perlu Anda perhatikan bahwa ada bilangan yang merupakan kelipatan dari 2, 3, 5, dan 7 yang bersamaan dan tetap diberi warna, sebab yang perlu difokuskan adalah kolom yang tidak berwarna. Dari tabel tersebut Anda bisa melihat kolom yang tidak berwarna berjumlah 26 kolom termasuk angka 1. Namun karena angka 1 bukanlah angka prima maka ada 25 angka prima dari bilangan 1-100.
25 bilangan prima tersebut adalah :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, dan 97.
Periksa di sini jika sedang mencari tempat les matematika di Jakarta Timur
Manfaat Bilangan Prima
Konsep bilangan prima ini sudah ada sejak zaman kuno. Para matematikawan di zaman Yunani kuno seperti Euclid dan Eratosthenes sudah mulai mempelajari sifat-sifat bilangan prima. Lalu pada abad pertengahan, para ilmuwan dari Arab dan Persia seperti Al-Khawarizmi dan Al-Farisi menemukan metode untuk mendapatkan bilangan prima besar.
Cek di sini untuk mempelajari pengertian sudut dalam matematika

Di era modern, bilangan prima menjadi sangat penting karena digunakan dalam berbagai aspek. Seperti kriptografi dan keamanan informasi. Untuk membuat kunci enkripsi yang kuat, maka diperlukan sifat-sifat bilangan prima dalam implementasinya. Selain itu bilangan prima juga menjadi subjek penelitian di berbagai cabang ilmu matematika seperti teori bilangan, teori graf, dan teori kompleksitas.
Bilangan prima juga memudahkan untuk mencari kelipatan persekutuan terkecil (KPK) dan faktor persekutuan terbesar (FPB). Apa yang dimaksud dengan KPK dan FPB? Bagaimana mencarinya menggunakan bilangan prima? Anda bisa mempelajarinya dengan les privat bersama guru matematika yang handal.
Contoh Soal Bilangan Prima
Soal A
Apakah 15 merupakan bilangan prima?
Jawab :
15 : 1 = 15
15 : 15 = 1
15 : 3 = 5
15 : 5 = 3
Maka 15 BUKAN merupakan bilangan prima karena memiliki faktor lebih dari dua yaitu 1, 3, 5, dan 15.
Soal B
Apakah 37 merupakan bilangan prima?
Jawab :
37 : 1 = 37
37 : 37 = 1
Maka 37 merupakan bilangan prima karena hanya memiliki dua faktor yaitu 1 dan 37.
Mempelajari bilangan prima sangatlah mudah, Anda hanya perlu mengetahui sifat-sifat bilangan prima maka Anda bisa menentukan apakah angka tersebut masuk ke bilangan prima atau tidak. Jika ingin mempelajari lebih lanjut, Anda bisa mengikuti les privat matematika dengan guru-guru terbaik di Superprof. Anda juga bisa mempelajari gradien loh.
Ringkaskan dengan AI



















Suka. Mudah dipahami
terima kasih atas apresiasi nya :)