
Sistem pertidaksamaan linear dua variabel berhubungan erat dengan pertidaksamaan linear dan persamaan linear dua variabel. Pemahaman yang baik tentang topik ini sangat penting karena dapat membantu siswa dalam memahami dan menyelesaikan berbagai masalah matematika yang melibatkan pertidaksamaan linear dua variabel.
Pertidaksamaan linear dua variabel adalah pertidaksamaan yang melibatkan dua variabel, yaitu x dan y. Pertidaksamaan linear dua variabel memiliki bentuk umum ax + by < c, dengan a, b, dan c adalah bilangan riil dan a, b tidak sama dengan nol. Pertidaksamaan linear dua variabel ini dapat digunakan untuk menggambarkan daerah di atas atau di bawah garis lurus di bidang koordinat. Sistem pertidaksamaan linear terdiri dari dua atau lebih pertidaksamaan linear. Untuk menyelesaikan sistem pertidaksamaan linear dua variabel, kita perlu mencari daerah yang memenuhi semua pertidaksamaan linear tersebut secara bersama-sama. Daerah ini sering disebut sebagai daerah solusi atau daerah penyelesaian.
Salah satu metode yang umum digunakan untuk menyelesaikan sistem pertidaksamaan linear dua variabel adalah dengan menggunakan grafik. Langkah pertama adalah menggambar grafik setiap pertidaksamaan linear pada sistem. Kemudian, kita perlu mencari titik potong (secara geometri) dari garis-garis yang mewakili setiap pertidaksamaan linear tersebut. Titik potong ini mewakili solusi dari sistem pertidaksamaan linear dua variabel.
Dalam kelas 10, siswa akan belajar tentang SPLDV atau Sistem Persamaan Linear dan Pertidaksamaan Dua Variabel. SPLDV menggabungkan konsep persamaan linear dua variabel dan pertidaksamaan linear dua variabel. Dalam SPLDV, siswa akan mempelajari tentang bagaimana menyelesaikan dan menginterpretasikan sistem persamaan dan pertidaksamaan linear dua variabel secara bersamaan. Siswa juga akan diajarkan mengenai metode eliminasi dan substusi untuk menyelesaikan SPLDV.
Cek di sini untuk sistem persamaan linear dua variabel dan sistem persamaan linear tiga variabel

Contoh Soal Pertidaksamaan Linear Dua Variabel
Contoh soal pertidaksamaan linear dua variabel sangat penting untuk Anda pelajari sebagai media latihan. Berikut adalah contoh soal pertidaksamaan linear dua variabel kelas 10:
- Tentukan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel berikut:
2x + y > 5
x - y < 3
- Carilah solusi dari sistem persamaan linear dua variabel berikut:
3x + 4y = 10
2x - y = 1
Kemampuan dalam menyelesaikan dan memahami SPLDV sangat penting dalam kehidupan sehari-hari. SPLDV dapat digunakan untuk memodelkan berbagai situasi dalam kehidupan nyata, seperti perencanaan anggaran, perencanaan produksi, dan analisis pasar. Dengan pemahaman yang baik tentang SPLDV, siswa akan dapat mengambil keputusan yang bijaksana dan memecahkan masalah secara efisien dalam kehidupan mereka.
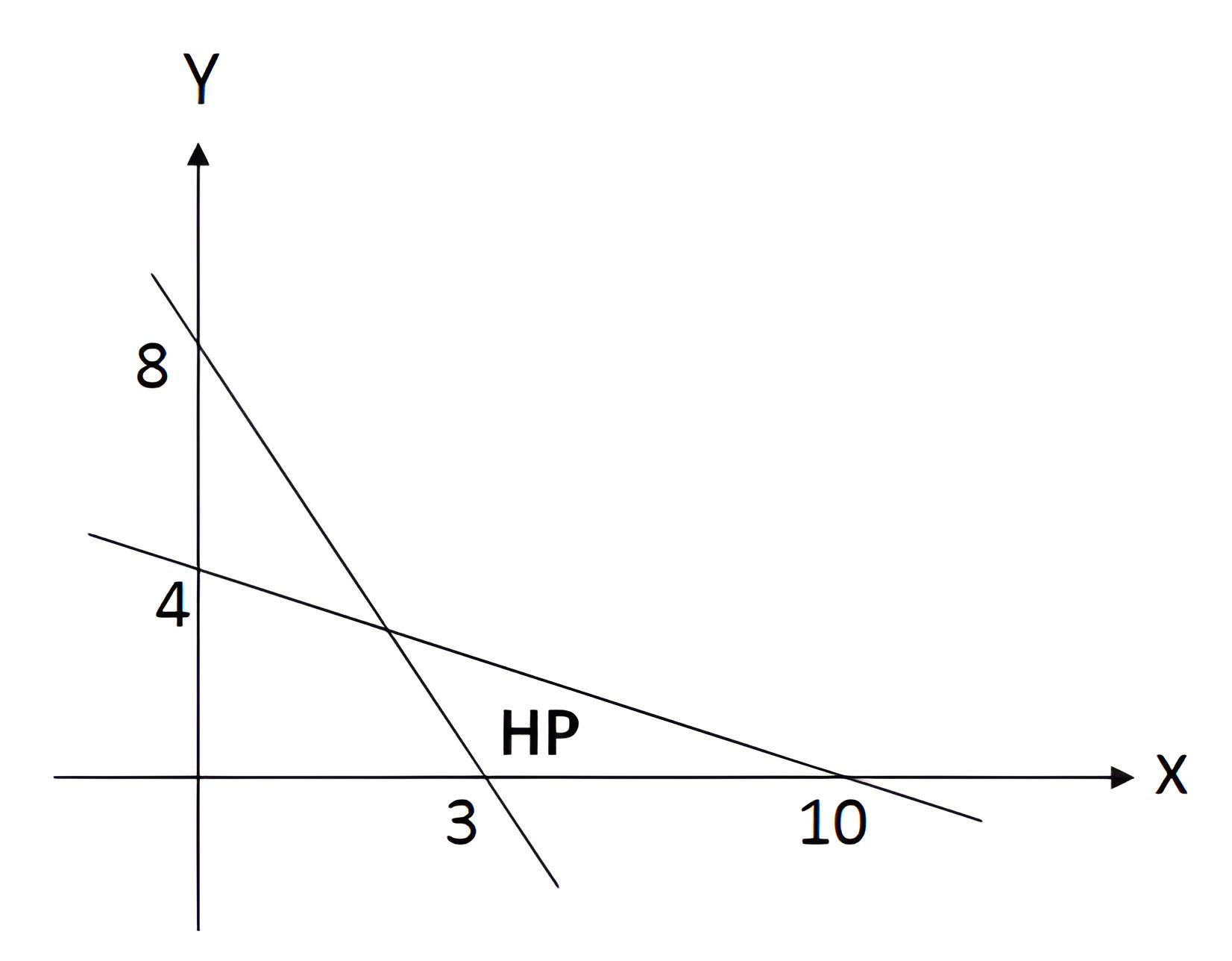
Memahami konsep ini akan membantu siswa dalam menyelesaikan berbagai masalah matematika dan juga dalam pengambilan keputusan dalam kehidupan nyata. Dengan belajar tentang SPLDV dalam kelas 10, siswa akan memiliki dasar yang kuat untuk menyelesaikan SPLDV yang lebih kompleks di tingkat yang lebih tinggi.
Periksa di sini untuk mempelajari grafik fungsi eksponensial
Sistem pertidaksamaan linear dua variabel
Sistem pertidaksamaan linear dua variabel adalah konsep dalam matematika yang melibatkan dua variabel dalam satu persamaan atau pertidaksamaan. Pertidaksamaan linear sendiri merupakan pernyataan matematis yang melibatkan variabel dengan tingkat pangkat satu. Dalam sistem pertidaksamaan linear dua variabel, terdapat dua persamaan atau pertidaksamaan yang harus diselesaikan secara bersama-sama.
Sistem pertidaksamaan linear dua variabel ini sering kali dijumpai dalam konteks masalah kehidupan sehari-hari. Misalnya, dalam perencanaan anggaran rumah tangga, kita mungkin perlu mencari tahu bagaimana membagi pengeluaran antara dua variabel, misalnya pengeluaran untuk makanan dan transportasi, dengan mempertimbangkan beberapa batasan dan pertimbangan. Dalam kasus ini, berlaku pertidaksamaan linear dua variabel yang harus kita selesaikan.
Salah satu metode yang digunakan untuk menyelesaikan sistem pertidaksamaan linear dua variabel adalah metode grafik. Metode ini melibatkan pembuatan grafik untuk setiap persamaan atau pertidaksamaan dan menentukan titik potong dari kedua garis tersebut. Titik potong ini kemudian dapat digunakan untuk menentukan solusi sistem pertidaksamaan linear dua variabel.
Misalkan kita memiliki sistem pertidaksamaan linear dua variabel berikut:
2x - 3y ≤ 6
x + y ≥ 2
Pertama-tama, kita perlu mengubah kedua pertidaksamaan menjadi persamaan linear yaitu mengganti tanda pertidaksamaan dengan tanda sama dengan. Kemudian, kita menggambar grafik untuk kedua persamaan ini pada koordinat kartesius. Garis yang mewakili persamaan pertama memiliki rumus y = (2/3)x - 2, sedangkan garis yang mewakili persamaan kedua memiliki rumus y = -x + 2.
Setelah menggambar kedua garis ini, kita mencari titik potong dari kedua garis tersebut. Titik potong ini adalah solusi sistem pertidaksamaan linear dua variabel kita. Dalam contoh ini, titik potong berada pada koordinat (3, -1). Namun, metode grafik ini hanya efektif jika sistem pertidaksamaan linear dua variabel memiliki solusi yang mudah ditentukan melalui grafik. Jika sistem pertidaksamaan linear dua variabel memiliki banyak batasan dan pertimbangan, mungkin diperlukan metode lain seperti metode substitusi atau metode eliminasi.
Cek di sini untuk mempelajari rumus perbandingan senilai

Contoh soal spldv kelas 10 biasanya mencakup berbagai masalah kehidupan nyata yang memerlukan penyelesaian menggunakan sistem pertidaksamaan linear dua variabel. Dalam kesimpulan, sistem pertidaksamaan linear dua variabel merupakan konsep matematika yang penting dalam pemecahan masalah kehidupan sehari-hari. Dengan menggunakan berbagai metode seperti metode grafik, metode substitusi, atau metode eliminasi, kita dapat menyelesaikan sistem pertidaksamaan linear dua variabel dan mendapatkan solusi yang tepat. Pemahaman tentang sistem pertidaksamaan linear dua variabel akan sangat berguna dalam kehidupan sehari-hari dan dalam penyelesaian masalah matematika.
Periksa di sini untuk les privat matematika jakarta timur
Ringkaskan dengan AI















