Hai Sobat Matematika! Apakah Anda pernah mendengar rumus simpangan baku? Tahukah Anda apa fungsi mencari simpangan baku dalam statistika? Simpangan baku merupakan saah satu rumus penting dalam matematika statistika. Tentu bagi Anda yang menyukai matematika, Anda tidak akan asing lagi dengan simpangan baku. Untuk mengetahui lebih lanjut tentang simpangan baku dan bagaimana cara mencari simpangan baku, yuk simak artikel berikut ini!
Jika Anda bekerja sebagai data analyst, atau Anda sangat menyukai ilmu statistik, tentu Anda tidak bisa melewatkan konsep simpangan baku ini. Dalam banyak kesempatan, rumus simpangan baku memiliki banyak fungsi yang dibutuhkan dalam kehidupan sehari-hari. Ini terutama dalam mencari atau mengukur tingkat kesamaan atau kedekatan dalam suatu kelompok. Berikut pengertian simpangan baku, cara menghitung simpangan baku, fungsi, rumus simpangan baku, hingga contoh-contoh soal yang dapat membantu Anda memahami konsep simpangan baku dalam ilmu statistika dengan lebih baik.
Jika Anda kesulitan dalam memahami materi matematika, jangan ragu untuk meminta bantuan para guru privat Superprof.
Anda perlu juga mengetahui pengertian dari integral tak tentu!

Pengertian Simpangan Baku
Sebelum mempelajari bagaimana cara mencari simpangan baku, pertama kita harus memahai pengertian dari simpangan baku.
Simpangan baku adalah salah satu teknik statistik untuk menjelaskan homogenates dari sebuah data kelompok. Simpangan baku atau standar deviasi merupakan nilai statistik yang dimanfaatkan untuk menentukan bagaimana sebaran data dalam sampel, serta seberapa dekat titik data individu ke mean (rata-rata nilai) sampel.
Nilai simpangan baku dari kumpulan data bisa = 0, lebih besar, atau lebih kecil dari nol (0).
- Jika simpangan baku = 0, maka semua nilai yang ada dalam himpunan tersebut adalah sama.
- Sedangkan jika nilai simpangan baku lebih besar atau lebih kecil dari nol menandakan bahwa titik data individu jauh dari nilai rata-rata.
Semakin dekat nilai individu suatu data dengan nilai rata-rata dari kelompok data tersebut, maka dapat disimpulkan bahwa nilai penyimpangannya juga semakin kecil. Sebaliknya apabila nilai individu suatu data dengan nilai rata-rata dari kelompok data tersebut semakin jauh, artinya penyimpangan semakin besar.
Tentu saja, pengertian simpangan baku ini sangat penting untuk dipahami agar lebih mudah dalam menggunakan rumus simpangan baku ke depannya.
Cek di sini untuk mengetahui statistika deskriptif
Fungsi

Simpangan baku atau yang sering disebut sebagai standar deviasi ini biasanya digunakan para ahli statistika untuk bisa mengetahui simpangan baku dari sebuah sampel data yang diambil dari populasi. Misalnya Anda ingin mengetahui simpangan baku dari berat badan anak di desa A. Maka tidak mungkin kita akan mengambil semua dari populasi tersebut karena mungkin waktu yang kita butuhkan akan sangat lama. Untuk mempersingkat waktu tersebut maka Anda bisa menggunakan rumus simpangan baku tersebut, karena dengan menggunakan rumus simpangan baku kita bisa mengetahui hanya dari sample data yang kita ambil. Sehingga tentu saja ini akan lebih memudahkan kita bukan? Ini akan membantu kita untuk mempermudah menemukan angka dari sebuah sampel data.
Maka dapat disimpulkan bahwa simpangan baku digunakan oleh para ahli statistik atau orang yang terjun dalam dunia statistik untuk mengetahui apakah sampel data yang diambil mewakili seluruh populasi. Karena dalam mencari data yang tepat untuk sebuah populasi sangat sulit dilakukan, maka untuk memepermudah mencarinya, dipilih sampel data yang mewakili seluruh populasi.
Periksa di sini untuk mengetahui cara mencari rata rata data kelompok
Cara Menghitung Simpangan Baku
Untuk mencari nilai simpangan baku ditentukan kepada jenis datanya apakah data kelompok atau data tunggal. Meskipun pada garis besar memiliki langkah-langkah yang sama, tapi cara membaca data tunggal dan data kelompok jelas berbeda.
Data tunggal adalah data yang disajikan secara lebih sederhana dan tidak dibedakan berdasarkan kelas-kelas interval. Secara garis besar, berikut langkah untuk menghitung simpangan baku dari sekelompok data tunggal, yakni;
- Menghitung nilai rata-rata dari setiap titik data yang ada. Nilai Rata-rata sama dengan jumlah dari setiap nilai yang ada dalam kumpulan data, kemudian kita bagi dengan jumlah total titik dari data tersebut.
- Menghitung penyimpangan untuk setiap titik data dari rata-ratanya. Yaitu dengan cara mengurangi nilai dari nilai rata-rata.
- Kemudian, Simpangan setiap titik data kita kuadratkan lalu kita cari penyimpangan kuadrat individu rata-ratanya. Nilai yang dihasilkan tersebut disebut varian.
- Simpangan baku adalah akarkuadrat dari nilai varian tersebut.
Sementara data kelompok merupakan kumpulan data dalam jumlah besar sehingga dikelompokkan ke dalam beberapa interval kelas. Untuk memudahkan pembacaan data kelompok maka penyajiannya menggunakan kelas frekuensi. Berikut cara menghitung simpangan baku dari data kelompok, yakni:
- Langkah pertama adalah mencari nilai rata-rata atau Mean dari data kelompok
- Selanjutnya kurangi nilai tengah dari kelas frekuensi data dengan nilai Mean. Hasil pengurangan data kemudian dikuadratkan
- Selanjutnya hasil kuadrat dari selisih data tersebut dikali dengan frekuensi dari kelas interval yang sedang dihitung (kelas interval ke-i)
- Seluruh nilai perhitungan dijumlahkan dan dibagi total datanya
- Nilai akhir yang didapatkan diakar kuadrat
Agar Anda lebih memahami bagaimana cara menari simpangan baku, perhatikan rumus simpangan berikut.
Cek di sini untuk mengetahui cara menentukan diskriminan pada persamaan kuadrat
Rumus Simpangan Baku
Rumus Simpangan Baku Data Populasi
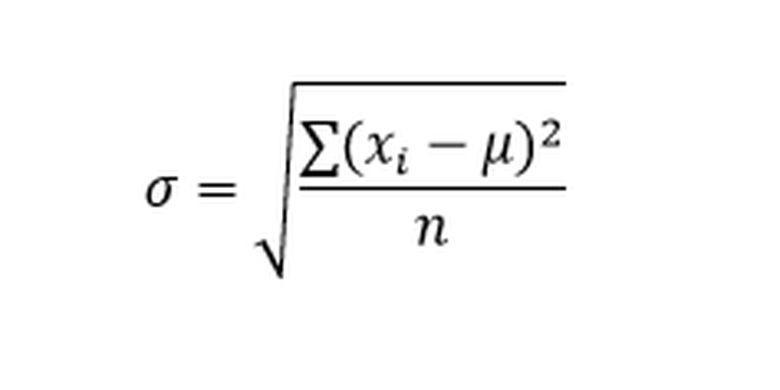
Rumus simpangan baku populasi. Foto: Akuntansi Manajemen Berbasis Desain oleh Subagyo
Keterangan:
σ (sigma) = simpangan baku populasi
Xi = data ke-i
μ = nilai rata-rata populasi
n = jumlah data pengamatan populasi
Rumus simpangan baku sampel
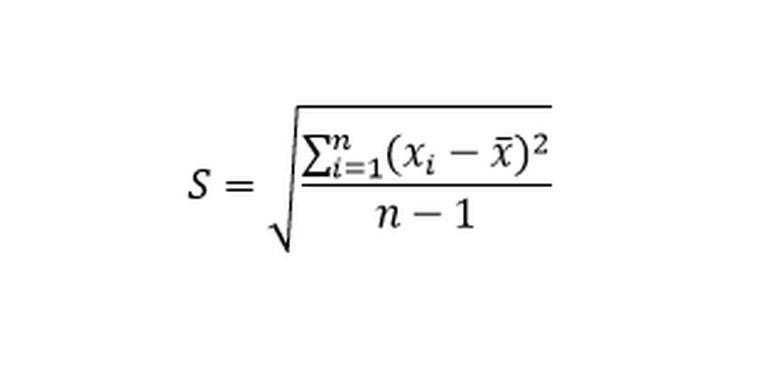
Rumus simpangan baku sampel. Foto: Statistika dalam Pendidikan dan Olahraga
Keterangan:
S = simpangan baku
Xi = nilai tengah
x = nilai rata-rata
n = jumlah data
Rumus simpangan baku data kelompok
Tidak hanya untuk data tungga, simpangan baku juga dapat dicari dari data berkelompok. Dilansir dari Cuemath, distribusi frekuensi harus diperhatikan dalam simpangan baku data kelompok. Sehingga, rumus simpangan bakunya menjadi:
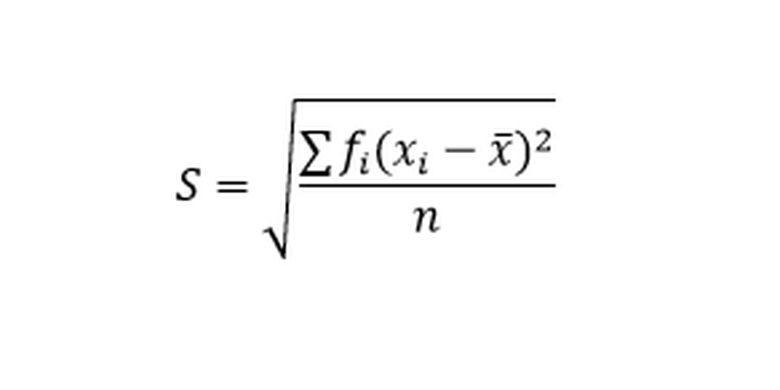
Rumus simpangan baku data kelompok. Foto: Statistika dalam Pendidikan dan Olahraga
Keterangan;
S: simpangan baku data kelompok
fi: frekuensi kelompok
xi: nilai data (I = 1, 2, 3, 4, 5, … )
x: nilai rata-rata (mean)
n: jumlah data
Periksa di sini untuk les matematika di Medan
Contoh Soal;
Soal : Vivi mengikuti ujian matematika sebanyak 10 kali dalam semester ini. Pada 10 kali ulangannya itu Vivi mendapatkan nilai ujian matematika sebagai berikut 91, 79, 80, 86, 75, 90, 88, 93, 100 dan 87. Berapakah simpangan baku dari nilai ujian matematikan vivi?
Jawab : Kita sudah mendapatkan data nilai ujian matematika Vivi yaitu 91, 79, 80, 86, 75, 90, 88, 93, 100 dan 87. Untuk bisa mengetahui nilai simpangan bakunya maka terlebih dahulu carilah nilai rata-rata dari nilai ujian vivi.
Rata – Rata = (91 + 79 + 80 + 86 + 75 + 90 + 88 + 93 + 100 + 87) / 10 = 859 / 10 = 85.9
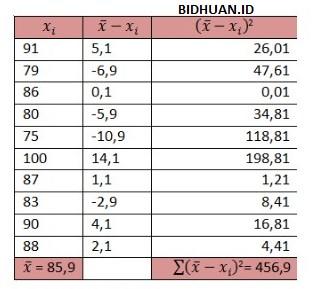
Setelah itu masukkan lagi ke dalam rumus seperti ini

Dari data yang tadi kita masukkan, kita sudah bisa menemukan nilai simpangan baku dari nilai ujian matematika Vivi yaitu 6,759. Seperti itulah menghitung cara menghitung rumus simpangan baku, sekarang Anda sudah memahaminya bukan? Jika ini sulit untuk Anda, jangan ragu untuk meminta bantuan ke kursus privat Superprof.
Periksa di sini jika sedang mencari tempat les matematika di Indonesia
Ringkaskan dengan AI