Garis singgung lingkaran adalah garis yang menyentuh lingkaran tepat di satu titik tanpa memotongnya. Memahami apa itu garis singgung lingkaran penting dalam matematika, terutama untuk menyelesaikan berbagai permasalahan geometris. Artikel ini akan membahas secara mendalam tentang rumus persamaan garis, sifat garis singgung lingkaran, rumus menghitung lingkaran, dan contoh soal agar pembelajaran lebih mudah dipahami. Selain itu, materi ini relevan untuk materi lingkaran kelas 8 hingga garis singgung lingkaran kelas 11.
Cek di sini untuk mempelajari standar deviasi

Pengertian Garis Singgung Lingkaran

Garis singgung lingkaran adalah garis yang hanya menyinggung lingkaran pada satu titik. Titik ini disebut titik singgung. Persamaan garis singgung dapat ditentukan jika persamaan lingkaran sudah diketahui, biasanya dalam bentuk:
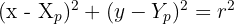
di mana:
• ( (X_p, Y_p) ) = pusat lingkaran
• ( r ) = jari-jari lingkaran
Karakteristik Garis Singgung Lingkaran :
1. Gradien Garis Singgung Lingkaran
Untuk membentuk rumus persamaan garis, gradien garis singgung (m) perlu diketahui. Persamaan umum garis singgung lingkaran:
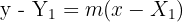
dengan ( (X_1, Y_1) ) adalah titik singgung pada lingkaran. Gradien ( m ) akan berbeda tergantung lokasi titik yang dilalui garis.
2. Titik Pada Lingkaran (k = 0)
Jika titik berada tepat pada lingkaran, hanya ada satu garis singgung pada lingkaran yang dapat dibentuk. Persamaan garis singgung melalui titik tersebut:
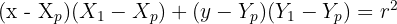
Artinya, garis singgung selalu tegak lurus terhadap jari-jari yang menghubungkan pusat lingkaran ke titik singgung.
3. Titik Di Luar Lingkaran (k > 0)
Jika titik berada di luar lingkaran, maka dua garis singgung dapat ditarik dari titik itu ke lingkaran. Gradien garis singgung dapat dicari melalui persamaan:
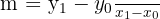
dengan ((x_0, y_0)) titik luar dan ((x_1, y_1)) titik singgung pada lingkaran.
Setelah gradien diketahui, persamaan garis singgung terbentuk:
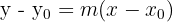
Panjang garis singgung dari titik luar ke titik singgung lingkaran dapat dihitung dengan:
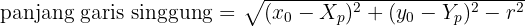
Periksa di sini untuk les matematika terbaik
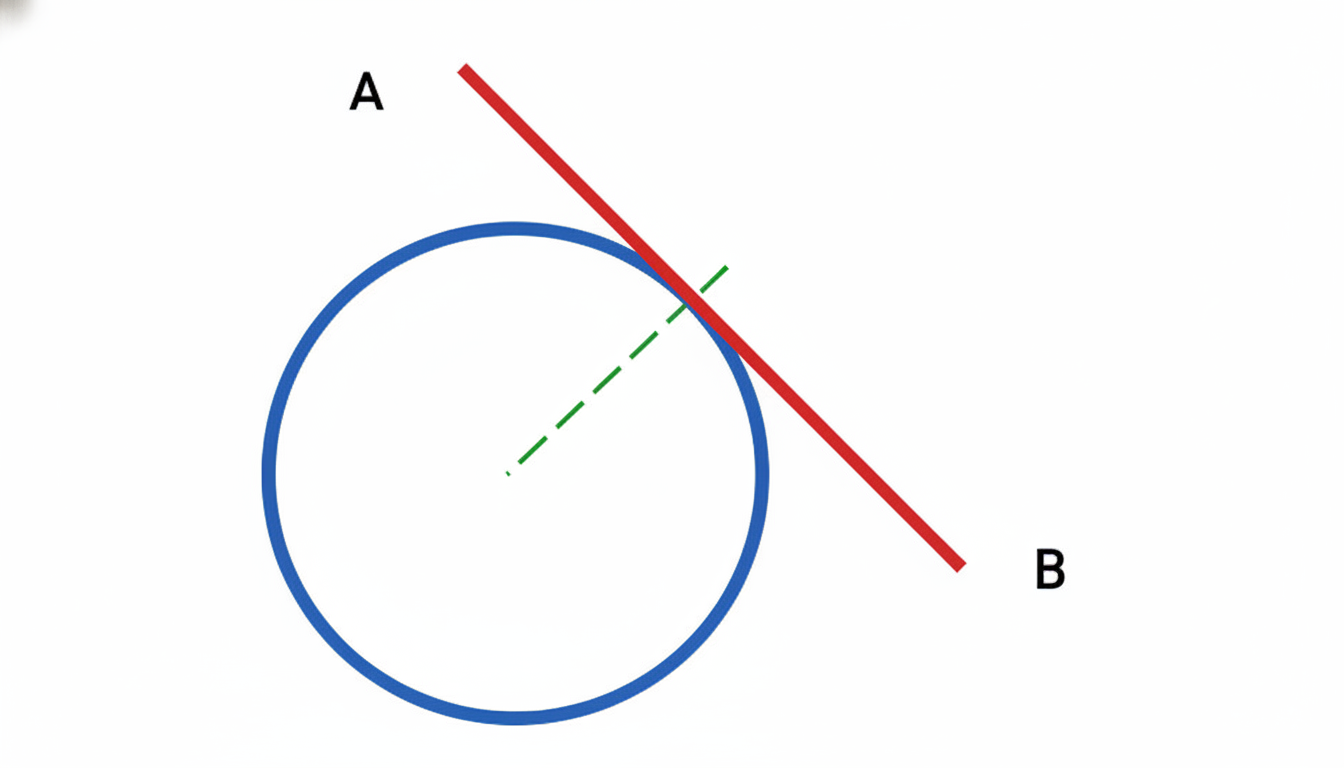
Pada gambar di atas, garis AB adalah garis singgung lingkaran. Garis tersebut hanya bersentuhan dengan lingkaran di titik A, membentuk sudut siku-siku dengan jari-jari lingkaran yang ditarik melalui titik singgung.
Konsep ini penting karena garis singgung lingkaran memiliki sifat yang unik, di mana garis tersebut tidak memotong atau melampaui lingkaran, tetapi hanya berinteraksi dengan titik singgung secara halus dan langsung. Hal ini memungkinkan garis singgung lingkaran digunakan dalam berbagai aplikasi yang membutuhkan sentuhan yang lembut dan presisi.
Dengan pemahaman yang mendalam tentang pengertian garis singgung lingkaran dan bagaimana konsep ini diterapkan dalam konteks matematika dan dunia nyata, kita dapat menghargai keindahan dan kegunaannya yang luas.
Periksa di sini untuk mempelajari barisan dan deret matematika
Sifat-sifat Garis Singgung:
Garis singgung pada lingkaran memiliki beberapa sifat penting yang perlu dipahami. Pertama, garis singgung selalu tegak lurus terhadap jari-jari yang menghubungkan pusat lingkaran ke titik singgung. Artinya, sudut antara garis singgung dan jari-jari selalu 90°.
Kedua, dari satu titik di luar lingkaran dapat ditarik dua garis singgung, yang panjangnya sama. Sifat ini sering digunakan dalam menghitung panjang garis singgung pada lingkaran dan dalam soal garis singgung persekutuan dua lingkaran.
Ketiga, hanya ada satu garis singgung yang melewati titik di lingkaran, sedangkan untuk titik di dalam lingkaran tidak dapat ditarik garis singgung. Sifat-sifat ini menjadi dasar dalam memahami sifat garis singgung lingkaran dan penerapan rumus garis singgung luar maupun persamaan garis singgung elips.
Jenis-Jenis Garis Singgung Lingkaran
Posisi garis singgung terhadap lingkaran bisa berbeda-beda, sehingga terbagi menjadi beberapa jenis. Memahami jenis-jenis garis singgung membantu dalam menentukan persamaan garis, menghitung gradien, perhitungan rumus busur lingkaran dan memecahkan soal-soal praktis dalam kehidupan sehari-hari maupun bidang teknik dan fisika. Berikut adalah penjelasan lengkap mengenai jenis-jenis garis singgung lingkaran:
Garis Singgung Melalui Titik pada Lingkaran
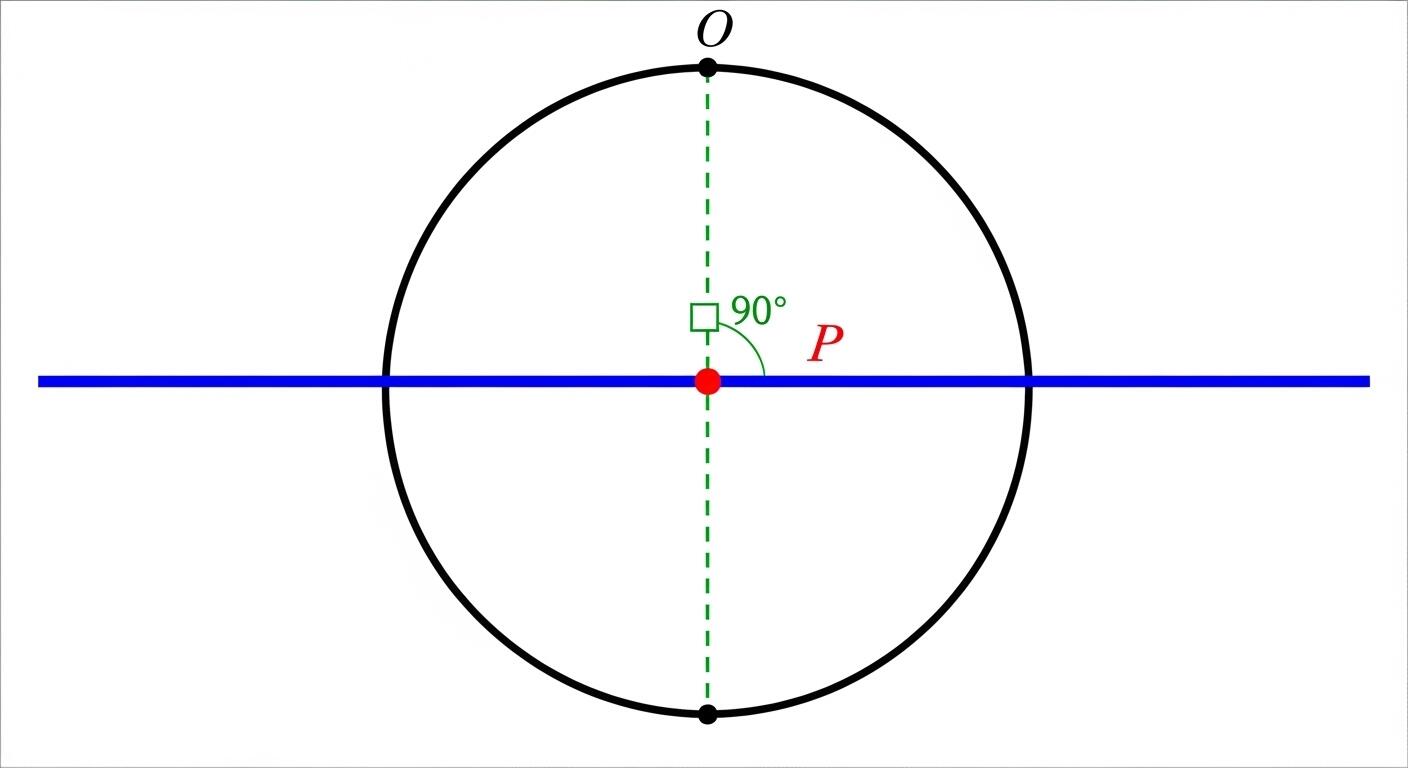
Garis singgung yang melalui titik tepat di lingkaran memiliki ciri utama: menempel di lingkaran dan tegak lurus terhadap jari-jari yang menuju titik singgung. Persamaan garis singgung ini dapat ditulis sebagai:
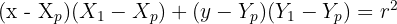
di mana:
• ((X_p, Y_p)) = pusat lingkaran
• (r) = jari-jari lingkaran
• ((X_1, Y_1)) = titik singgung
Contoh Soal:
Tentukan persamaan garis singgung lingkaran ((x-2)^2 + (y-3)^2 = 16) yang melalui titik ((6,3)).
Penyelesaian Singkat:
• Tentukan pusat ((X_p, Y_p) = (2,3)) dan jari-jari (r = 4).
• Gunakan rumus: ((x - 2)(6 - 2) + (y - 3)(3 - 3) = 16)
• Sederhanakan: (4(x - 2) + 0 = 16 \implies x - 2 = 4 \implies x = 6) Jadi, persamaan garis singgung adalah (x = 6).
Garis Singgung dengan Gradien Tertentu
Jika gradien (m) garis singgung diketahui, persamaan garis singgung dapat ditulis:
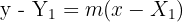
Titik ((X_1, Y_1)) adalah titik singgung pada lingkaran. Garis ini terlihat seakan memotong lingkaran, namun hanya menyinggung di satu titik. Gradien (m) menentukan kemiringan garis sehingga tetap bersinggungan dengan lingkaran. Contoh penerapan ini penting untuk persamaan garis singgung elips maupun lingkaran.
Contoh Soal:
Lingkaran: ((x-1)^2 + (y+2)^2 = 25)
Gradien garis singgung: (m = 2)
Tentukan persamaan garis singgung.
Penyelesaian Singkat:
• Gradien garis singgung (m = 2).
• Gunakan persamaan: ((y - Y_1) = m (x - X_1)) • Substitusi titik singgung ((X_1, Y_1)) yang memenuhi persamaan lingkaran, kemudian tentukan persamaan lengkap garis singgung.
Garis Singgung dari Titik di Luar Lingkaran
Untuk titik di luar lingkaran ((x_0, y_0)), dua garis singgung dapat dibuat. Gradien (m) dihitung dari persamaan:
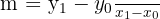
Setelah gradien diperoleh, persamaan garis singgung:
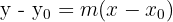
Panjang garis singgung dari titik luar ke titik singgung dapat dihitung dengan:
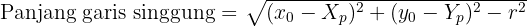
Contoh Soal:
Tentukan persamaan garis singgung dari titik ((10, 5)) ke lingkaran ((x-3)^2 + (y-2)^2 = 16).
Penyelesaian Singkat:
• Hitung jarak titik luar ke pusat lingkaran: (\sqrt{(10-3)^2 + (5-2)^2} = \sqrt{49 + 9} = \sqrt{58})
• Panjang garis singgung: (\sqrt{58 - 16} = \sqrt{42}) • Tentukan gradien (m) untuk kedua garis singgung, lalu tulis persamaan masing-masing garis: (y - 5 = m(x - 10))
Persamaan Garis Singgung Lingkaran

Persamaan matematis dari garis singgung lingkaran bervariasi tergantung pada titik singgung dan letak lingkaran. Namun, ada beberapa prinsip dasar yang dapat membantu dalam menentukan persamaan garis singgung pada lingkaran.
Salah satu rumus yang umum digunakan untuk menentukan persamaan garis singgung pada lingkaran adalah:
y = mx + c
Di mana:
m adalah gradien (slope) dari garis singgung.
c adalah konstanta.
Untuk menentukan nilai gradien m, kita dapat menggunakan rumus gradien garis:
m = - a/b
Di mana:
a adalah koefisien dari titik singgung.
b adalah koefisien y dari titik singgung.
Cek di sini untuk mempelajari nilai mutlak
Rumus Garis Singgung Lingkaran
Selain persamaannya, terdapat juga rumus yang dapat digunakan untuk menentukan garis singgung lingkaran. Rumus ini bergantung pada koordinat pusat lingkaran (h, k) dan jari-jarinya r. Rumus ini disebut sebagai persamaan lingkaran umum:
(x - h)^2 + (y - k)^2 = r^2
Dengan menggunakan rumus ini dan dengan memperhatikan titik singgung, kita dapat menemukan persamaan garis singgung pada lingkaran dengan lebih mudah.
Untuk menemukan rumus persamaan garis singgung lingkaran, kita dapat menggunakan rumus persamaan garis singgung lingkaran yang telah disebutkan sebelumnya. Dengan mengetahui titik singgung dan menggunakan rumus gradien, kita dapat menentukan persamaan garis singgung pada lingkaran dengan tepat.
Tentu, berikut ini adalah contoh soal mengenai garis singgung lingkaran beserta solusinya:

Contoh Soal
1. Diberikan lingkaran dengan persamaan (x - 2)^2 + (y + 3)^2 = 25. Tentukan persamaan garis singgung lingkaran tersebut yang melalui titik (4, 1).
Solusi:
Langkah pertama adalah menentukan koordinat pusat lingkaran (h, k) dan jari-jarinya r. Dari persamaan lingkaran, kita dapatkan bahwa h = 2, k = -3, dan r = 5.
Kemudian, kita gunakan rumus gradien untuk menentukan gradien garis singgung. Rumus gradien m = - a/b, di mana a adalah koefisien x dari titik singgung dan b adalah koefisien y dari titik singgung.
Titik singgung yang diberikan adalah (4, 1), maka a = 4 - 2 = 2 dan b = 1 + 3 = 4.
m = - 2/4 = - 1/2
Sekarang, kita punya gradien m = - 1/2. Kita dapat menggunakan rumus y = mx + c untuk menentukan konstanta c. Kita sudah memiliki nilai m dan titik singgung (4, 1), maka kita bisa substitusi nilainya ke dalam rumus:
1 =(- 1/2) x 4 + c
1 = -2 + c
c = 1 + 2 = 3
Sehingga, persamaan garis singgung lingkaran adalah y = -(1/2)x + 3.
Dengan demikian, kita telah menentukan persamaan garis singgung lingkaran yang melalui titik yang diberikan.
2. Diberikan lingkaran dengan persamaan (x - 3)^2 + (y + 4)^2 = 36. Tentukan persamaan garis singgung lingkaran tersebut yang tegak lurus dengan garis (y = 2x - 1).
Solusi:
Langkah pertama adalah menentukan koordinat pusat lingkaran (h, k) dan jari-jarinya (r). Dari persamaan lingkaran, kita dapatkan bahwa (h = 3), (k = -4), dan (r = 6).
Kemudian, kita harus mencari gradien garis singgung yang tegak lurus dengan garis (y = 2x - 1). Gradien garis tegak lurus dengan gradien (m) dapat ditemukan dengan gradien garis tegak lurus dari garis y yaitu -1/m. Dalam kasus ini, (m = 2), maka -1/m = -1/2).
Sekarang, kita harus menemukan titik singgung antara garis singgung dan lingkaran. Kita tahu bahwa garis singgung dan garis (y = 2x - 1) harus saling bersinggungan. Oleh karena itu, kita perlu mencari titik singgung yang memenuhi kedua persamaan.
Substitusi persamaan lingkaran ke dalam persamaan garis tegak lurus dan cari titik-titik yang memenuhi kedua persamaan. Setelah itu, kita dapat menemukan persamaan garis singgung.
y = -1/2x + c
Substitusi persamaan lingkaran ke dalam persamaan garis tegak lurus:
(x - 3)^2 + (y + 4)^2 = 36
(x - 3)^2 + (-1/2x + c + 4)^2 = 36
Dari sini, kita dapat mencari titik singgung dengan menggabungkan kedua persamaan tersebut dan menyelesaikan sistem persamaan. Setelah titik singgung ditemukan, kita dapat menentukan nilai (c) dan akhirnya mendapatkan persamaan garis singgung.
Jika Anda memerlukan bantuan lebih lanjut dalam menyelesaikan masalah ini atau memiliki pertanyaan lainnya, jangan ragu untuk bertanya!
Periksa di sini jika sedang mencari les matematika terdekat di Medan
Garis Singgung Persekutuan Dua Lingkaran

Dalam geometri, selain garis singgung pada satu lingkaran, kita juga mengenal garis singgung persekutuan dua lingkaran. Garis ini adalah garis lurus yang menyinggung kedua lingkaran sekaligus, sehingga hanya “menyentuh” masing-masing lingkaran pada satu titik.
Garis singgung persekutuan dibagi menjadi dua jenis, yaitu:
Garis Singgung Persekutuan Luar
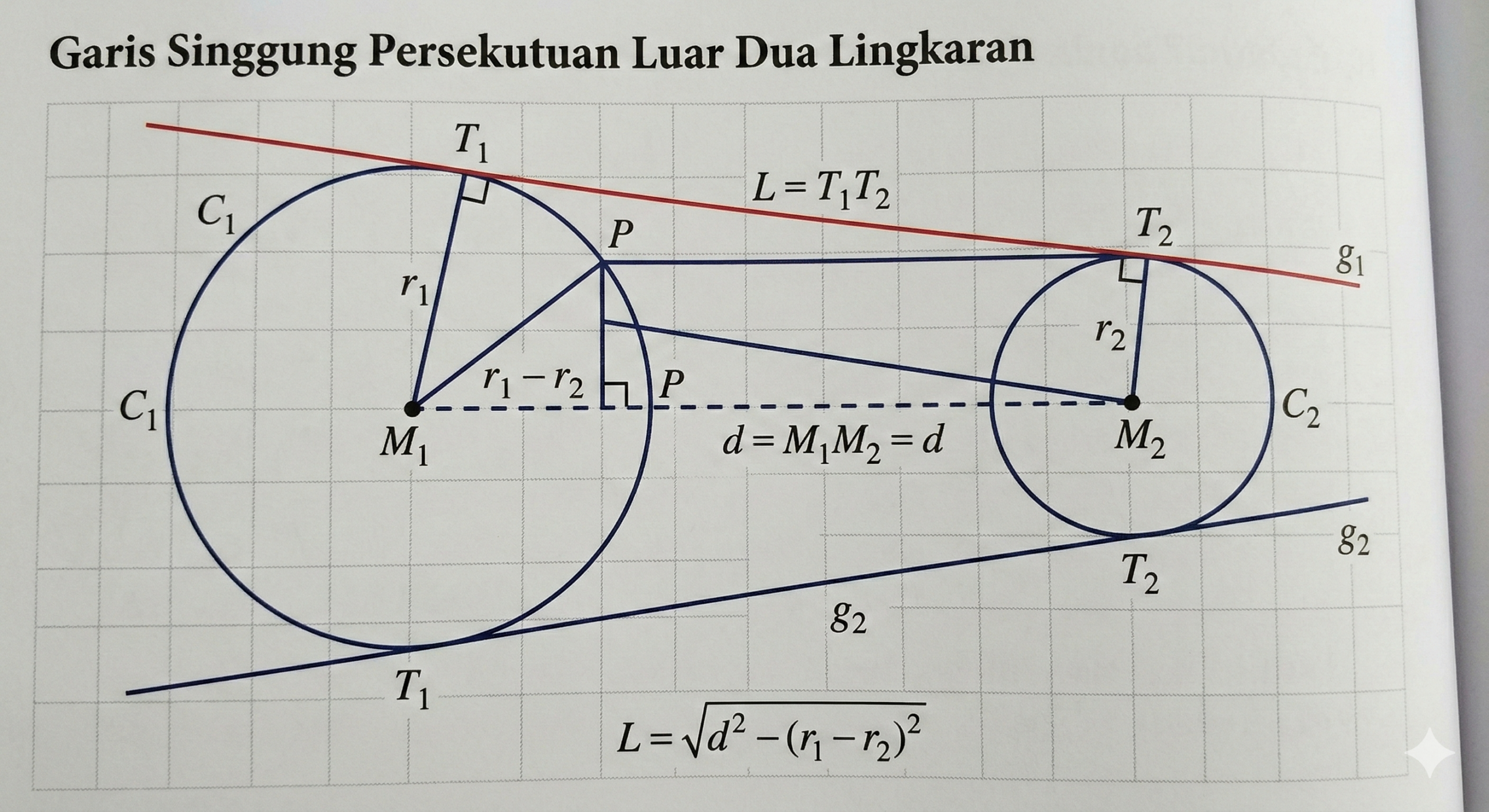
Sama seperti garis singgung persekutuan dalam, garis singgung persekutuan luar juga melibatkan dua lingkaran yang berbeda ukuran. Namun, perbedaannya terletak pada posisi garis singgungnya. Garis singgung persekutuan luar akan menyentuh kedua lingkaran pada titik yang terletak di sisi yang sama dari kedua lingkaran tersebut. Garis singgung ini terletak di luar kedua lingkaran dan menghubungkan dua titik singgung yang berada di sisi luar lingkaran.
Secara matematis, panjang rumus garis singgung luar antara dua lingkaran dapat dihitung dengan rumus:

Keterangan:
- l adalah panjang garis singgung persekutuan luar,
- d adalah jarak antara pusat kedua lingkaran,
- R adalah jari-jari lingkaran besar,
- r adalah jari-jari lingkaran kecil.
Rumus panjang garis singgung persekutuan luar ini digunakan untuk menghitung panjang garis singgung yang terletak di luar dua lingkaran. Sebagai perbandingan dengan rumus untuk garis singgung persekutuan dalam, rumus ini memperhitungkan jumlah jari-jari kedua lingkaran, yang membuat garis singgung berada di luar kedua lingkaran.
Ciri khas garis singgung persekutuan luar : titik singgung berada di sisi yang sama pada kedua lingkaran. Garis ini tegak lurus terhadap jari-jari pada titik singgung masing-masing lingkaran.
Contoh Soal:
Mari kita lihat beberapa contoh soal yang melibatkan garis singgung persekutuan luar untuk memahami cara penggunaan rumus-rumus tersebut.
Diketahui:
• Jarak pusat dua lingkaran (d = 13 , \text{cm})
• Jari-jari lingkaran besar (R = 6 , \text{cm})
• Jari-jari lingkaran kecil (r = 1 , \text{cm})
Hitung panjang garis singgung persekutuan luar.
Penyelesaian:

Jadi, garis singgung persekutuan luar = 12 cm.
Garis Singgung Persekutuan Dalam
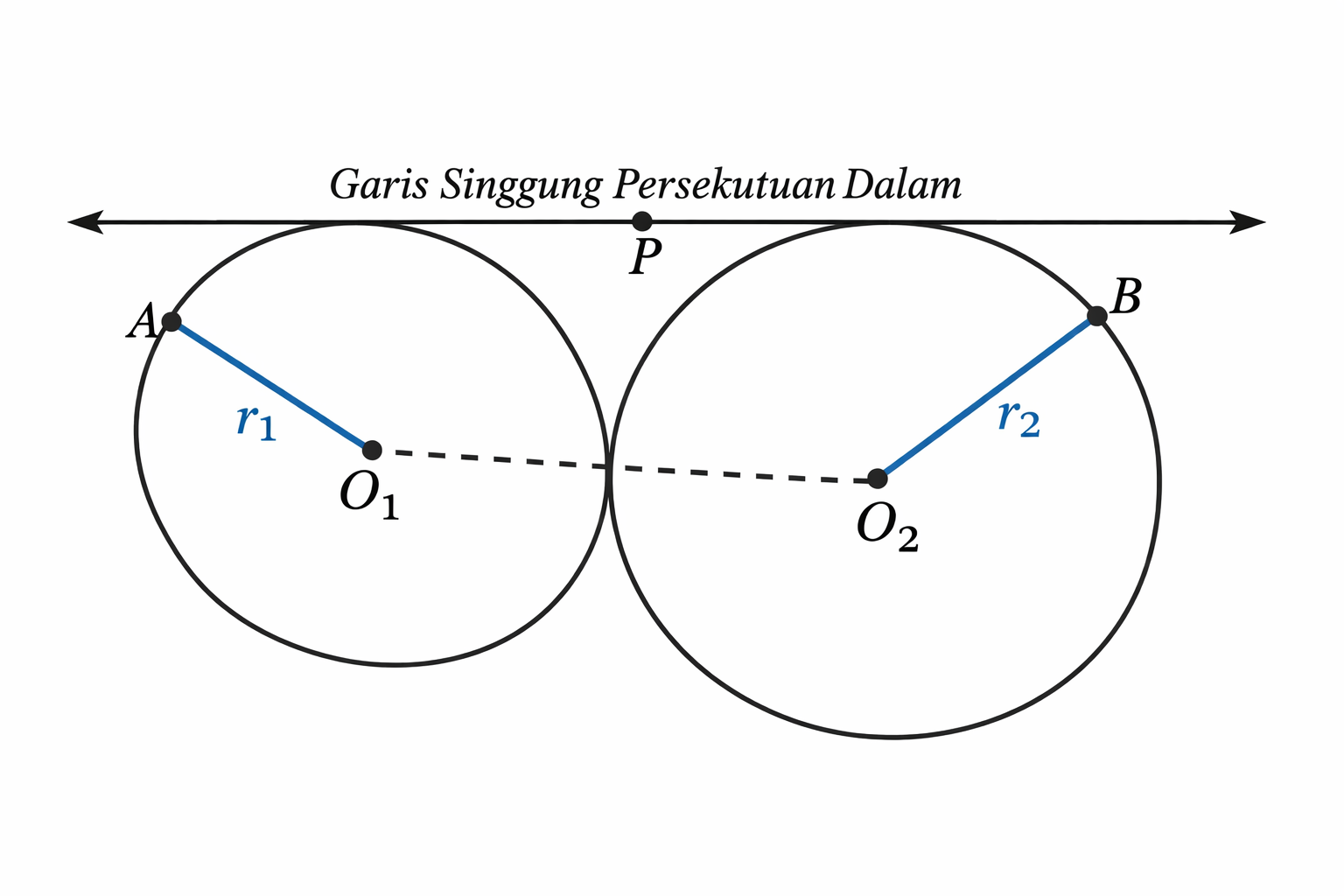
Garis singgung persekutuan dalam melibatkan dua lingkaran yang berdekatan, di mana garis singgung ini hanya menyentuh kedua lingkaran tersebut pada satu titik pada masing-masing lingkaran. Posisi garis persekutuan dalam dalam berada di antara dua lingkaran tersebut, menghubungkan kedua titik singgung yang terletak di sisi yang berlawanan.
Panjang garis singgung persekutuan dalam (GSPD) dapat dihitung dengan rumus:
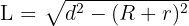
Keterangan:
• (L) = panjang garis singgung persekutuan dalam
• (d) = jarak antar pusat kedua lingkaran
• (R) = jari-jari lingkaran besar
• (r) = jari-jari lingkaran kecil
Dengan rumus ini, kita dapat menghitung panjang garis singgung yang menghubungkan dua lingkaran yang berada di posisi berdekatan, dengan memperhatikan perbedaan ukuran kedua lingkaran dan jarak antar pusat lingkaran.
Ciri khas garis singgung persekutuan dalam : titik singgung berada di sisi yang berlawanan pada kedua lingkaran. Sama seperti garis singgung persekutuan luar, garis ini tegak lurus terhadap jari-jari di titik singgung.
Contoh Soal:
Mari kita lihat beberapa contoh soal yang melibatkan garis singgung persekutuan dalam untuk memahami cara penggunaan rumus-rumus tersebut.
Diketahui:
• Jarak pusat dua lingkaran (d = 15 , \text{cm})
• Jari-jari lingkaran besar (R = 7 , \text{cm})
• Jari-jari lingkaran kecil (r = 4 , \text{cm})
Hitung panjang garis singgung persekutuan dalam.
Penyelesaian:
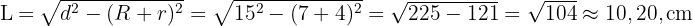
Jadi, garis singgung persekutuan dalam = 10,20 cm.
Perhatikan tabel rumus garis singgung persekutuan dalam dan luar jika tidak ingin menyesal :
| Jenis Garis Singgung | Rumus Panjang | Konsep Utama |
|---|---|---|
| Garis Singgung Persekutuan Luar (GSPL) | (L = \sqrt{d^2 - (R - r)^2}) | Panjang dipengaruhi oleh selisih jari-jari |
| Garis Singgung Persekutuan Dalam (GSPD) | (L = \sqrt{d^2 - (R + r)^2}) | Panjang dipengaruhi oleh jumlah jari-jari |
Contoh Soal Garis Singgung Persekutuan Dalam dan Luar
Dua lingkaran dengan jari-jari masing-masing 7 cm dan 5 cm memiliki jarak antara pusat kedua lingkaran 14 cm. Hitunglah panjang garis singgung persekutuan dalam dan garis singgung persekutuan luar!
Pembahasan:
Diketahui:
- R = 7 cm (jari-jari lingkaran besar),
- r = 5 cm (jari-jari lingkaran kecil),
- d = 14 cm (jarak antara pusat kedua lingkaran).
- Panjang garis singgung persekutuan dalam:
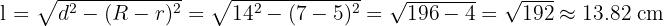
- Panjang garis singgung persekutuan luar:
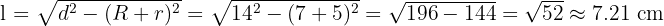
Jadi, panjang garis singgung persekutuan dalam adalah sekitar 13.82 cm dan panjang garis singgung persekutuan luar adalah sekitar 7.21 cm.
• Melalui Titik pada Lingkaran ((X_1, Y_1))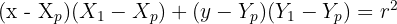
( (X_p, Y_p) ) = pusat lingkaran
( r ) = jari-jari
((X_1, Y_1)) = titik singgung
• Dengan Gradien Tertentu (m)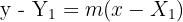
((X_1, Y_1)) = titik singgung
( m ) = gradien garis singgung
• Panjang Garis Singgung dari Titik di Luar Lingkaran ((x_0, y_0))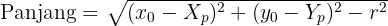
Aplikasi Garis Singgung Lingkaran dalam Kehidupan Sehari-hari

Garis singgung lingkaran bukan hanya konsep matematika abstrak, tetapi juga banyak diterapkan dalam berbagai bidang praktis. Menguasai rumus menghitung lingkaran dan garis singgung pada lingkaran membantu merancang sistem, mekanisme, dan struktur yang efisien serta aman.
Bidang Teknik dan Rekayasa
Dalam dunia teknik dan rekayasa, garis singgung lingkaran digunakan untuk merancang sistem mekanis, transportasi, dan struktur bangunan. Contoh penerapannya antara lain:
- Roda gigi (gear) dan sabuk transmisi (belt drive), di mana titik singgung menentukan kontak dan transmisi daya antar komponen.
- Sistem pengereman pada kendaraan, untuk menentukan sudut dan posisi gesekan yang optimal.
- Perancangan tikungan rel kereta api dan jalan, agar kendaraan melaju dengan aman melalui belokan.
- Desain geometris pada jembatan dan bangunan, guna memastikan titik kontak atau tumpuan struktur tepat dan stabil.
Dengan menerapkan prinsip garis singgung, insinyur dapat mengoptimalkan efisiensi, keamanan, dan ketahanan sistem atau konstruksi.
Bidang Astronomi
Dalam astronomi, garis singgung lingkaran digunakan untuk menghitung orbit planet, bulan, dan satelit. Konsep ini membantu menentukan:
- Titik di mana orbit sebuah benda langit bersinggungan dengan lintasan benda lainnya.
- Sudut dan posisi yang tepat untuk manuver satelit agar tetap stabil dalam orbit.
- Perhitungan lintasan planet atau komet ketika bergerak di sekitar matahari atau planet lain.
Penerapan garis singgung dalam astronomi memungkinkan ilmuwan memodelkan gerak benda langit dengan presisi tinggi, serta merancang misi antariksa yang aman dan efisien.
Periksa di sini untuk mempelajari translasi matematika
Video Pembelajaran Garis Singgung Lingkaran
Untuk memperdalam pemahaman Anda, berikut adalah video pembuktian rumus garis singgung persekutuan luar dua lingkaran:
Pembuktian Rumus Garis Singgung Persekutuan Luar Dua Lingkaran :
Belajar Bersama Superprof
Jika Anda tertarik untuk mendalami lebih lanjut tentang garis singgung lingkaran dan konsep matematika lainnya, jangan ragu untuk belajar bersama tutor profesional di Superprof, atau Anda bisa memilih les matematika surabaya untuk mendapatkan pendampingan yang tepat.
Dengan pemahaman yang mendalam tentang garis singgung lingkaran, Anda dapat menggali keindahan matematika dan mengaplikasikannya dalam berbagai konteks yang menarik dan bermanfaat.
Ringkaskan dengan AI
















