Baik Anda sedang belajar untuk Statistik AP, ujian SBMPTN, atau hanya memerlukan bantuan ekstra dalam mengerjakan tugas, soal latihan ini akan memberi panduan ekstra yang Anda perlukan. Meskipun metode analisis statistik dan pemodelan statistik sering dikaitkan langsung dengan analisis data, penting untuk memahami aritmatika yang mendasari metode analitik ini.
Meskipun sebagian besar paket perangkat lunak, seperti SPSS dan Stata memerlukan sedikit atau bahkan tidak memerlukan perhitungan apa pun atas nama ahli statistik, penting untuk mengetahui cara kerja dari perangkat lunak ini. Inti dari sebagian besar analisis statistik adalah cabang matematika yang disebut statistik Bayesian. Anda tentunya tidak harus mempelajari teorema Baye setelah kursus pengantar statistik pertama, namun penting bagi Anda untuk selalu mengingat implikasi teorema yang dikenal sebagai inferensi Bayesian.
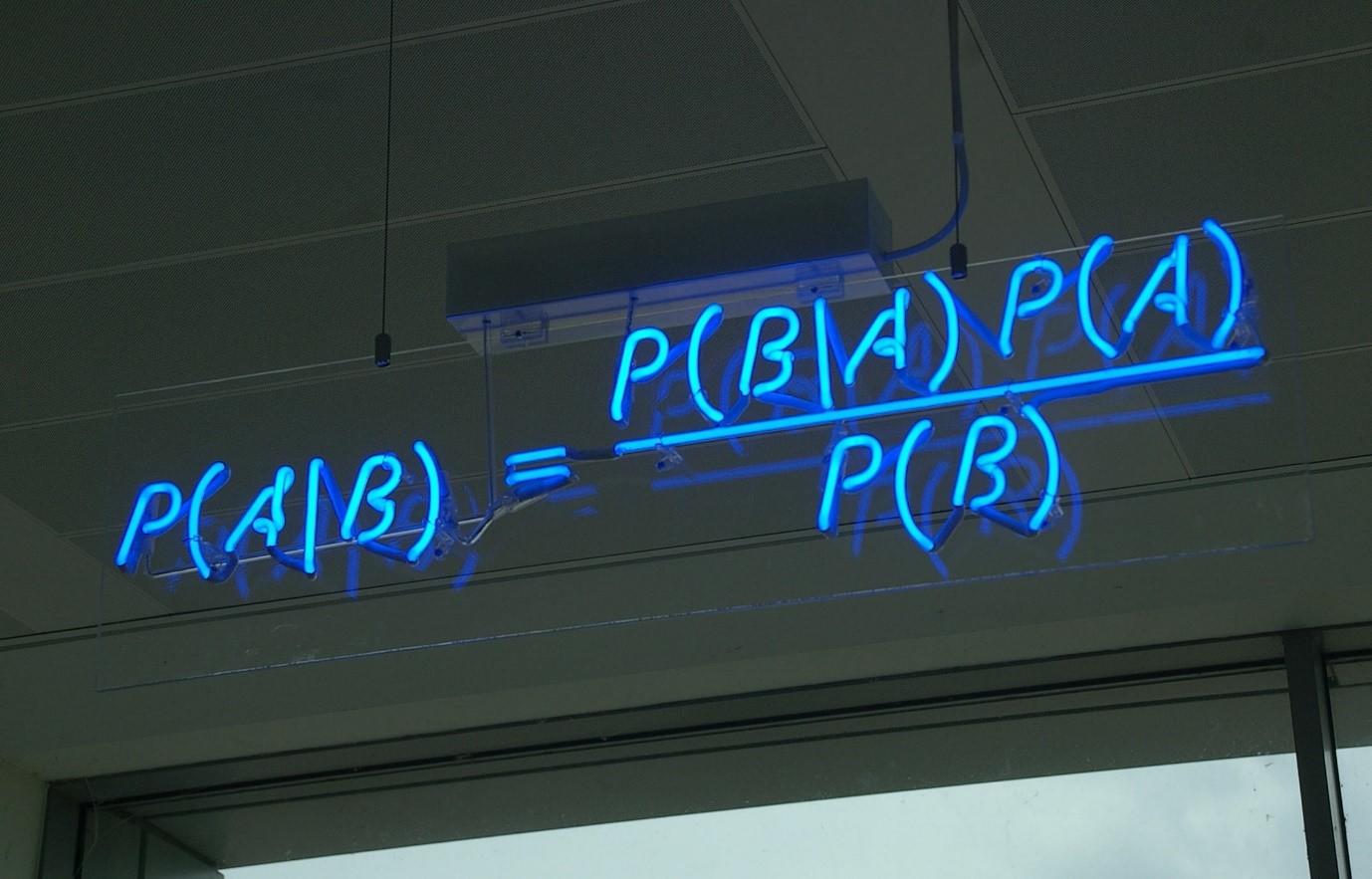
Teorema Bayes menggunakan probabilitas untuk mendeskripsikan kemungkinan suatu peristiwa terjadi berdasarkan informasi sebelumnya tentang peristiwa sama yang terjadi, yang juga disebut prior. Misalnya, jika Anda ingin menghitung probabilitas truk es krim di lingkungan Anda yang melintas pada hari itu, mengingat hari itu cerah, Anda dapat menggunakan data empiris sebelumnya untuk memperkirakan seberapa besar kemungkinan Anda akan mendapatkan es krim hari ini.
Jadi, definisi inferensi Bayes adalah mendeduksi kemungkinan suatu peristiwa dari sebaran populasi menggunakan teorema Baye. Ini adalah dasar dari banyak soal dan pengujian statistik yang akan Anda temui, dan penting untuk diingat karena sering kali Anda tidak akan melihatnya secara eksplisit. Panduan ini akan menawarkan tiga bagian contoh yang berangkat dari teori ini, masing-masing bagian dibangun berdasarkan teori ini.
Pelajari tentang kursus statistik online disini

Komputasi Statistik Dasar
Untuk mengerjakan soal latihan di bagian ini, penting untuk memahami statistik dasar. Kemungkinan besar, Anda telah mengenal probabilitas dan memahami pentingnya probabilitas bersyarat dalam membangun analisis data eksplorasi yang paling sederhana sekalipun. Statistik dan probabilitas berjalan beriringan, oleh karena itu penting untuk memahaminya sebelum mempraktikkan soal-soal ini.
Definisi dan keterampilan yang perlu Anda pahami untuk menyelesaikan masalah pada bagian ini meliputi:
- Teori Batas Sentral
- Tendensi Sentral
- Distribusi Normal Standar
- Mean, Median dan Modus Sampel
Pertanyaan 1: Buatlah Plot Kotak Berdasarkan Plot Batang dan Daun Berikut
Plot kotak dan diagram batang serta daun merupakan cara berbeda dalam menampilkan distribusi variabel tertentu dalam data Anda. Bedanya, plot kotak menampilkan bagaimana data Anda didistribusikan berdasarkan distribusi normal. Untuk dapat membangun plot kotak, penting untuk memahami apa yang diwakili oleh setiap titik pada plot.
Median adalah bagian tengah, dengan 1, 2, 3, dan 4 mewakili empat kuartil berbeda pada data Anda. Artinya, jika kita mengambil kuartil pertama, berarti 25% data Anda berada di region ini. Pada kuartil 3, ini berarti 75% data Anda berada pada titik tersebut dan di bawahnya. Kuartil 0 mewakili minimum dan kuartil 4 mewakili maksimum. Ini kemudian dibandingkan dengan distribusi normal:
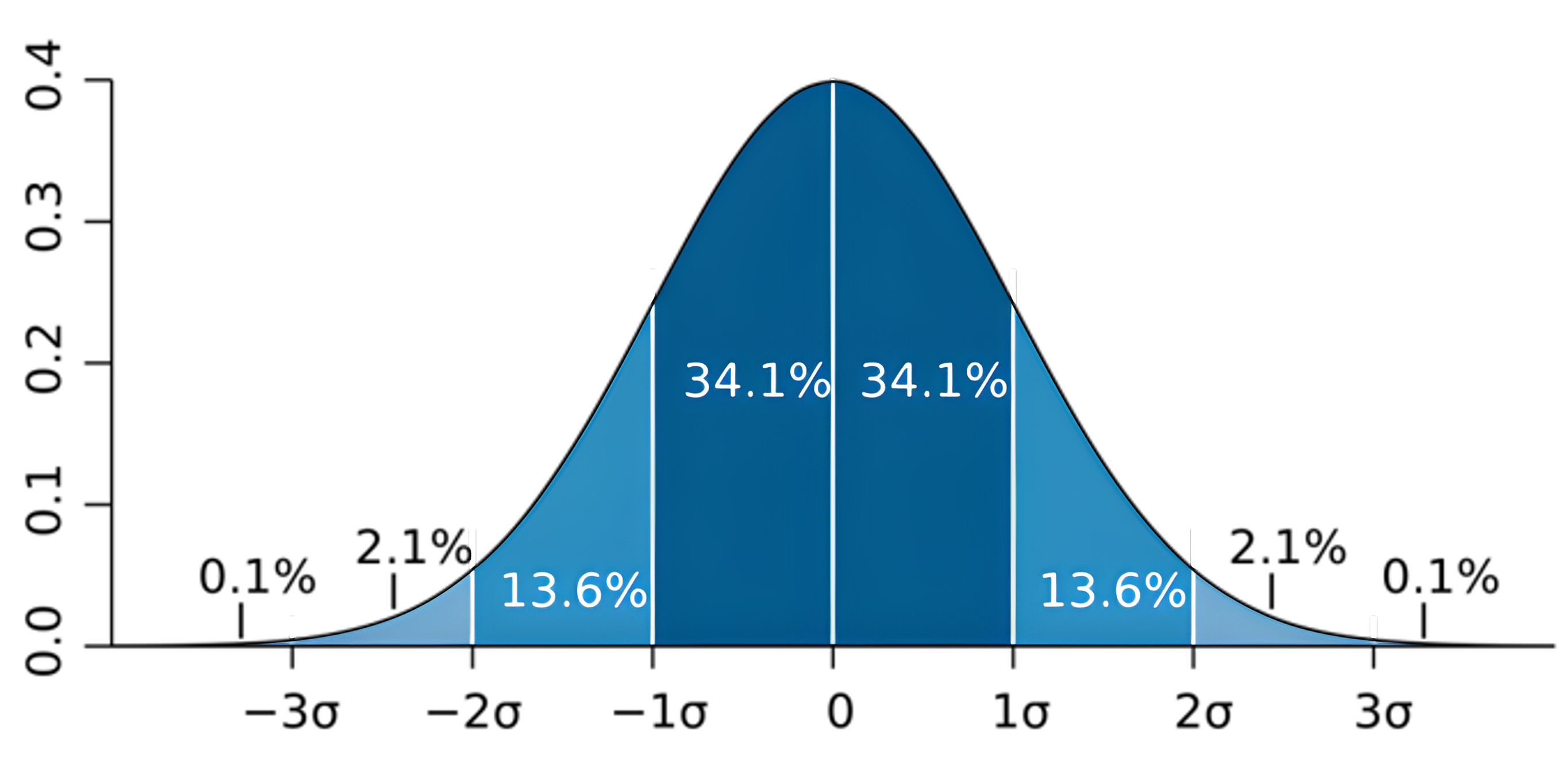
Dari gambar di atas, kita dapat melihat bahwa sekitar 50% data kita akan berada di antara Q1 dan Q3. Di bawah Q1 atau di atas Q3, hanya sekitar 25% dari data kami. Di luar batas minimum dan maksimum, titik data ini dianggap outlier. Outlier adalah suatu titik data yang tidak normal dalam kaitannya dengan populasi sampel. Dengan memahami informasi ini, kita dapat menghitung berdasarkan plot batang dan daun berikut:

Plot kotak kami terlihat sebagaimana berikut:
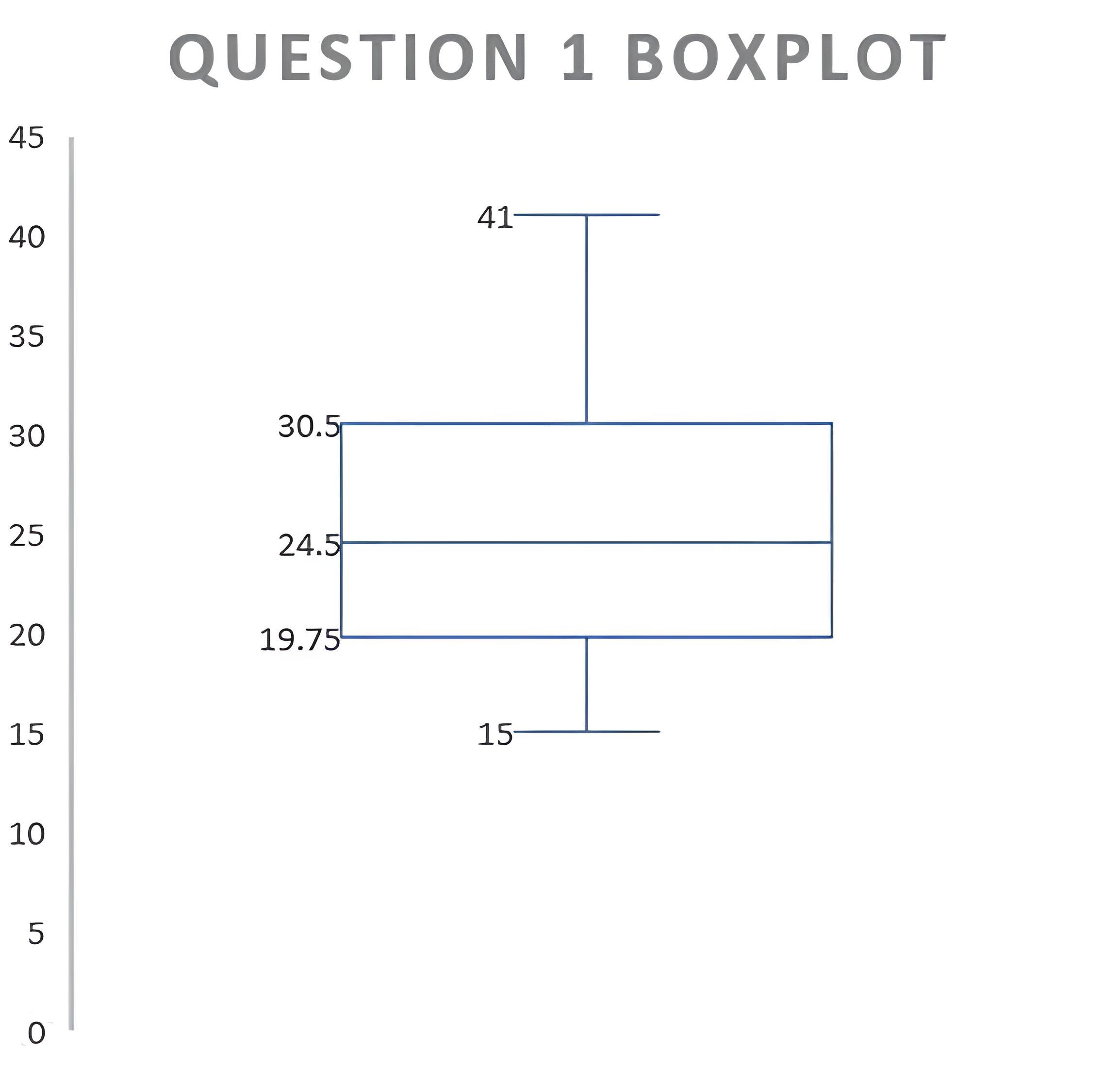
Pertanyaan 2: Cara Menghitung dan Menafsirkan Koefisien Korelasi
Berdasarkan bagian terakhir, penting untuk memahami bagaimana variabel tertentu dalam kumpulan data berhubungan satu sama lain. Hal ini sangat berguna karena apa pun jenis data yang didapati, Anda akan dapat menerapkan alat ini terlepas jenis konsep statistik apa pun yang Anda gunakan. Salah satu tabel penting yang akan Anda temui adalah tabel korelasi dan kovarians antar variabel dalam kumpulan data Anda.
Definisi korelasi adalah kekuatan hubungan antara dua variabel, sedangkan kovarians mengacu pada bagaimana kedua variabel tersebut bervariasi. Tujuan dari angka-angka ini adalah untuk dapat mengukur seberapa erat hubungan setiap variabel satu sama lain.
Misalnya, jika Anda memiliki kumpulan data terkait anak-anak sehat di sekolah SMA, tinggi badan dan berat badan kemungkinan besar akan memiliki korelasi yang tinggi. Di sisi lain, variabel seperti tinggi badan dan warna favorit mungkin tidak memiliki korelasi yang tinggi. Dalam model regresi, penghitungan dan interpretasi koefisien korelasi sangatlah penting.
Tabel yang paling umum terlihat adalah sebagai berikut, dan disebut Tabel Korelasi Produk Pearson:
| Favourite colour | Height | Weight | Femaile | |
|---|---|---|---|---|
| Favourite colour | 1 | |||
| Height | 0,15 | 1 | ||
| Weight | 0,04 | 0,87 | 1 | |
| Female | 0,57 | 0,76 | 0,84 | 1 |
Tabel korelasi bisa menjadi mudah jika Anda menguasai cara menafsirkan dan menganalisisnya
Angka-angka pada tabel mewakili koefisien korelasi, yang merupakan ukuran seberapa kuat hubungan antar variabel dalam tabel tersebut. Untuk menghitung koefisien korelasi, satu-satunya faktor yang Anda perlukan hanyalah deviasi standar sampel dan kovarians sampel.
Deviasi standar adalah ukuran seberapa jauh data Anda tersebar di sekitar rata-rata, berbeda dengan kesalahan standar, yaitu seberapa jauh data Anda tersebar di sekitar rata-rata, bukan berdasarkan data sampel, melainkan berdasarkan populasi sebenarnya.
Sebaliknya, kovarians adalah ukuran variasi dua variabel, yang sangat bergantung pada data sampel Anda. Kovariansi tidak sama dengan varians, yang hanya mengukur bagaimana satu variabel bervariasi dalam suatu kumpulan data.
Interpretasi koefisien korelasi mengikuti tiga aturan dasar. Yang pertama adalah angka-angka sepanjang diagonal harus selalu berjumlah satu. Diagonal mewakili korelasi antara variabel dengan variabel itu sendiri, yang harus selalu 1 atau 100%. Misalnya korelasi antara variabel warna favorit dengan variabel yang sama adalah 100%.
Aturan kedua adalah bahwa korelasi yang lebih tinggi dari 50% dianggap sebagai korelasi yang tinggi, sedangkan di bawah 50% dianggap sebagai korelasi yang lemah. Dalam contoh ini, meskipun warna favorit hanya memiliki korelasi 4% dengan berat badan, berat badan dan tinggi badan memiliki korelasi kuat hampir 90%.
Aturan ketiga adalah, meskipun korelasi di bawah 50% biasanya dianggap lemah, bukan berarti korelasi tersebut tidak menarik bagi Anda. Dalam contoh ini, warna favorit memiliki korelasi sebesar 57% dengan gender. Meskipun korelasinya tidak terlalu kuat jika dibandingkan dengan tabel di atas, hal ini menunjukkan adanya perbedaan gender yang mungkin perlu diselidiki lebih lanjut.
Anda dapat mulai mengikuti kursus ilmu data hari ini.
Pertanyaan 3: Cara Menafsirkan Tes Statistik
Statistik, seperti yang mungkin Anda ketahui, sangat bergantung pada informasi yang telah Anda pelajari. Oleh karena itu, penting untuk menguasai dasar-dasar statistik sebelum Anda dapat mulai memahami dan mempraktikkan uji statistik.
Penafsiran uji statistik akan berbeda-beda bergantung pada pengujian yang Anda lakukan. Dua tes paling umum yang akan Anda pelajari di awal aktivitas Anda di bidang statistik adalah:
- Uji Chi-Kuadrat
- Uji-T
Kedua pengujian tersebut melibatkan pengujian hipotesis, yang menggunakan statistik untuk menguji apakah variabel dalam data terkait atau tidak. Uji-t membandingkan rata-rata dua variabel dan memberi Anda wawasan tentang hubungan kedua variabel tersebut. Misalnya, ketika membandingkan obat baru dan plasebo, skor kesehatan dua kelompok pasien dapat dianalisis menggunakan uji-t.
Sebaliknya, uji chi-kuadrat dapat digunakan untuk menentukan apakah distribusi data sampel cocok dengan suatu populasi, atau apakah dua variabel dalam tabel kontingensi saling berkaitan satu sama lain.
Uji pertama disebut uji kesesuaian chi-kuadrat, sedangkan uji lainnya disebut uji chi-kuadrat terkait independensi nya. Contoh uji chi-kuadrat untuk independensi dapat ditemukan ketika mencoba melihat apakah tingkat pendidikan berhubungan dengan status perkawinan dengan membandingkannya dalam tabel kontingensi.
Jika Anda bingung tentang pengujian apa yang harus dilakukan untuk kumpulan data Anda, lihat panduan berikut ini!
Dapatkan Bantuan Statistik Lanjutan
Untungnya, ada banyak sumber daya yang dapat memberikan tips dan tutorial berguna jika Anda kesulitan dengan statistik. Mulai dari berbagai platform online, seperti Superprof dan Ruang Guru, hingga buku teks dan bahan bacaan lainnya. Salah satu sumber yang bagus untuk mendapatkan bantuan statistik tambahan secara online adalah Wolfram Math and Statistics How To. Kedua platform online tersebut tidak hanya memaparkan komponen matematika dari konsep statistika, tetapi juga menjelaskannya secara detail.
Jika Anda memerlukan penjelasan lebih lanjut, kunjungi Youtube untuk membantu Anda. Jika Anda mencari tutorial video yang bermanfaat, sebaiknya cari kata kunci dari istilah statistik yang sulit Anda gunakan dan telusuri untuk melihat video mana yang memiliki materi terbaik. Jika Anda lebih suka seseorang menjelaskannya kepada Anda secara langsung, les tatap muka menjadi pilihan yang bagus. Cara terbaik untuk memanfaatkan hal ini adalah dengan tidak takut untuk meminta bantuan tambahan dari guru Anda. Setiap orang belajar dengan kecepatan dan cara yang berbeda, jadi penting untuk mengingat hal itu saat Anda melanjutkan perjalanan belajar statistik Anda.
Résumer avec l'IA :















