Matematika merupakan disiplin ilmu wajib yang dipelajari siswa dari tingkat paling dasar hingga perguruan tinggi. Mengapa? Karena matematika merupakan ilmu dasar bagi disiplin ilmu lainnya. Untuk itu, memiliki ketertarikan lebih untuk belajar matematika tentu akan membantu kita tingkatkanlah semangat belajar matematika dan raih prestasi.
Tentu saja, matematika SD, SMP, hingga SMA jelas berbeda. Meskipun memiliki sub materi yang sama, namun penjabaran dan pembahasannya akan lebih luas dan mendalam. Misalnya, materi matematika bangun datar yang sudah dipelajari sejak siswa di bangku Sekolah Dasar. Namun, bangun datar yang dipelajari yang ditingkat berikutnya jauh lebih detail.
Di SD, siswa mungkin sudah mengenal macam-macam bangun datar, mulai dari persegi, persegi panjang, segitiga, trapesium, lingkaran, dll. Selain mengenali bentuknya, pada tingkat yang sama, siswa akan belajar cara menghitung luas dan keliling. Namun, berbeda dengan materi lingkaran kelas 11 yang akan berfokus pada persamaan lingkaran, dan bagaimana hubungan antara perpotongan garis dengan lingkaran. Persamaan lingkaran kelas 11 akan menjelaskan hubungan antara variabel x dan variabel y yang titik-titiknya membentuk sebuah lingkaran.
Teruslah membaca untuk mengetahui seputar materi lingkaran kelas 11! Jika Anda mengalami kesulitan saat belajar matematika, jangan ragu untuk meminta bantuan guru privat. Kursus privat akan menyusun program belajar yang disesuaikan dengan kebutuhan dan keinginan Anda belajar.
Dapatkan les privat matematika terbaik, hanya di Superprof.
Pengertian Lingkaran
Dalam ilmu matematika, lingkaran merupakan salah satu bangun geometri yang penting. Di samping persegi, persegi panjang, segitiga, trapesium, layang-layang, ataupun belah ketupat, lingkaran merupakan sub materi yang luas untuk dipelajari.
Lingkaran adalah tempat keduudkan titik yang mempunyai jarak sama terhadap titik tertentu dalam bidang datar. Titik tertentu yang dimaksudkan adalah pusat lingkaran, dan jarak yang dimaksud adalah jari-jari lingkaran. Bangun datar yang tersusun dari kurva dan bukan garis lurus sehingga tidak termasuk poligon inilah yang disebut dengan lingkaran.
Mudah bagi kita untuk membedakan lingkaran dengan bentuk bangun datar lainnya. Bangun datar ini adalah satu-satunya bangun datar yang tidak memiliki titik sudut. Jika dilihat dari ciri-cirinya, lingkaran memiliki diameter yang membaginya menjadi dua sisi seimbang dan jumlah sudutnya sebesar 180 derajat. Lingkaran juga memiliki satu sisi dengan simetri lipat lingkaran yang tak terhingga dan simetri putra lingkaran yang pun tak terhingga.
Dalam berbagai bidang, konsep mengenai lingkaran ini banyak diterapkan dalam kehidupan sehari-hari. Misalnya, luas lingkaran yang umumnya digunakan untuk mengukur lahan atau objek yang berbentuk lingkaran. Lebih jauh, lingkaran dapat digambar dalam diagram kartesius dan dinyatakan dalam bentuk persamaan lingkaran, sebagaimana persamaan garis. Untuk mengetahui rumus persamaan lingkaran dan semua yang berkaitan dengan itu, yuk simak penjelasan berikutnya!
Kenali juga pengertian fungsi dan invers dalam matematika!
Unsur-Unsur Lingkaran Kelas 6 SD
Masih ingat Pelajaran kelas 6 SD dulu? Pelajaran yang membahas tentang unsur-unsur pada lingkaran terdiri dari sebagai berikut :
- Titik Pusat
- Jari-jari
- Diameter
- Tali Busur
- Busur
- Juring
- Tembereng
- Apotema
Persamaan Lingkaran
Jika diilustrasikan dengan lebih detail, lingkaran pada dasarnya merupakan sekumpulan titik yang tak terhingga jumlahnya dan masing-masing memiliki jarak yang sama terhadap suatu titik pusat. Titik-titik inilah yang membentuk lingkaran. Berikutnya, persamaan lingkaran yang mempresentasikan koordinat dan ttik pusat, serta seluruh titik-titik yang membentuk keliling lingkaran tersebut.
Dilansir dari dari buku karya Tim Ganesha Operation “Pasti Bisa Matematika untuk SMA/MA Kelas XI”, bentuk persamaan lingkaran ditentukan oleh letak pusat lingkaran dan panjang jari-jarinya. Sebagaimana yang dijelaskan sebelumnya, persamaan lingkaran menyatakan hubungan antara variabel x dan variabel y yang titik-titiknya membentuk sebuah lingkaran.
Ada beberapa bentuk standar persamaan lingkaran yang berbeda karena memiliki situasi yang berbeda. Diantaranya:
Persamaan lingkaran dengan pusat pada titik O(0,0) dan jari-jari r
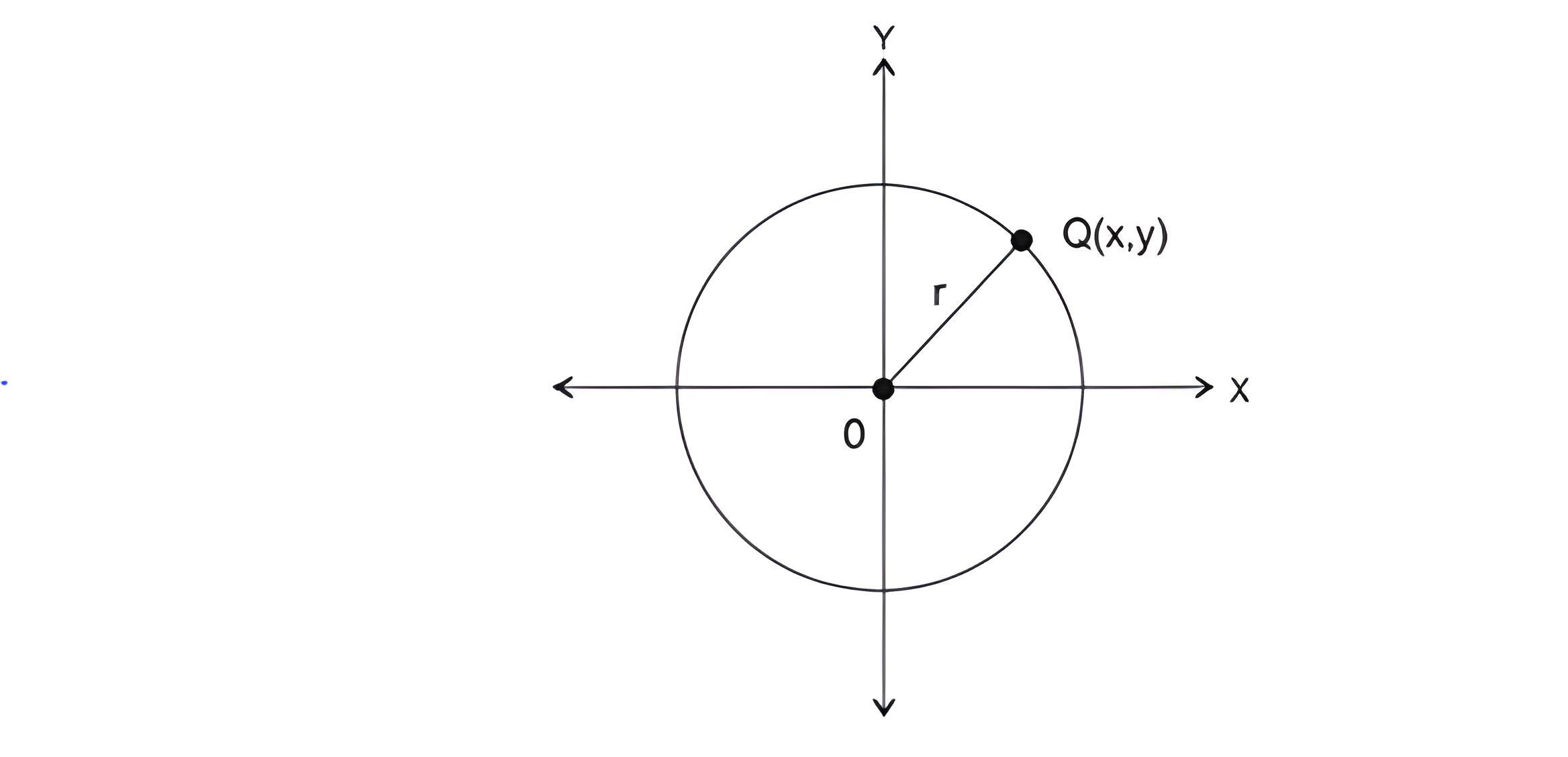
Jika titik pusat lingkaran berada tepat di perpotongan sumbu x dan sumbu y diagram kartesius atau titik (0,0), maka menggunakan rumus persamaan lingkaran pusat 0 0 berikut ini :
x2 + y2 = r2
Keterangan;
x = koordinat satu titik keliling lingkaran terhadap sumbu x
y = koordinat satu titik keliling lingkaran terhadap sumbu y
r = jari-jari lingkaran
Persamaan lingkaran dengan pusat P(a,b) dan jari-jari r
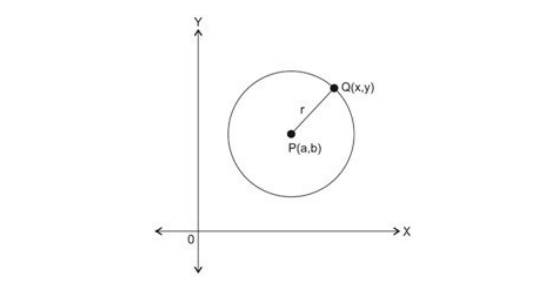
Gambar di atas menunjukkan bahwa lingkaran tidak berada tepat di titik (0,0), sehingga titik pusat lingkaran memiliki koordinat yang harus diperhitungkan dalam menghitung persamaan lingkarannya. Dari gambar tersebut juga dapat terlihat bahwa titik pusat lingkaran berada pada titik P(a,b), sementara satu titik lainnya yang berada di keliling lingkaran dengan Q(x,y). Maka dengan menggunakan rumus persamaan lingkaran sebelumnya, didapatkan;
r2 = x2 + y2..... (persamaan sebelumnya)
r2 = (x - a)2 + (y - a)2..... (pers. lingkaran dengan pusat P(a,b) dan jari-jari r)
r = √((x - a)2 + (y - a)2)
Pahami juga materi tentang aturan trigonometri untuk menambah pengetahuan Anda!
Persamaan Lingkaran Melalui 3 Titik
Selain menggunakan pusat dan jari-jari untuk menentukan persamaan lingkaran, ada juga metode lain yang tidak kalah pentingnya, yaitu persamaan lingkaran melalui 3 titik. Metode ini sangat berguna ketika kita hanya diberikan tiga titik yang terletak pada keliling lingkaran dan ingin mencari persamaannya. Dengan mengetahui koordinat ketiga titik tersebut, kita dapat menggunakan rumus determinan untuk menyusun persamaan lingkaran yang melalui ketiga titik tersebut.
Pendekatan ini memberikan cara alternatif yang lebih praktis dalam situasi tertentu, terutama ketika pusat lingkaran tidak diketahui secara langsung. Metode ini juga mengajarkan kita pentingnya pemahaman tentang hubungan geometris dalam sistem koordinat, di mana tiga titik yang tidak sebaris dapat dengan mudah membentuk sebuah lingkaran.
Bentuk Umum Persamaan Lingkaran
Selain bentuk standar persamaan lingkaran yang berbeda berdasarkan pusat lingkaran tersebut, ada juga bentuk umum persamaan lingkaran. Salah satu hal yang sangat penting dalam mempelajari persamaan lingkaran adalah mengetahui rumus titik pusat dari lingkaran tersebut.
Titik pusat adalah titik yang terletak di tengah lingkaran, dan setiap titik pada lingkaran memiliki jarak yang sama terhadap titik pusat ini. Dalam persamaan lingkaran, titik pusat sering kali diwakili oleh koordinat (h, k), yang mempermudah kita dalam menggambar dan menganalisis kedudukan lingkaran pada bidang koordinat. Rumusnya adalah;
x2 + y2 + Ax + By + C = 0
Dilihat dari persamaan di atas, maka dapat ditentukan rumus jari-jari lingkaran adalah;
r = √(1/4 A2 + 1/4 B2 - C)
Selanjutnya, dalam materi persamaan lingkaran, kita juga akan mempelajari cara mencari titik pusat lingkaran. Jika pusat lingkaran berada di titik P(a, b), persamaan lingkaran dapat dihitung menggunakan rumus mencari titik pusat lingkaran sebagai berikut ;
Pusat (-1/2 A,-1/2 B)
Penerapan Rumus Titik Pusat dalam Sistem Koordinat Non-Kartesian
Selain sistem koordinat kartesius, rumus titik pusat juga dapat diterapkan dalam sistem koordinat non-kartesian, seperti sistem koordinat polar. Dalam sistem polar, titik pusat biasanya dianggap sebagai asal (0,0), dan jari-jari lingkaran diukur dari titik pusat tersebut. Meskipun demikian, rumus titik pusat dalam koordinat kartesius tetap dapat digunakan untuk memetakan dan menggambarkan lingkaran dalam sistem koordinat polar dengan melakukan konversi antara kedua sistem tersebut.
Untuk membantu Anda memahami rumus persamaan lingkaran dan dapat menyelesaikan berbagai permasalahan terkait persamaan lingkaran, cobalah perhatikan contoh soal berikut ini dan jawablah latihan soalnya!
Cek disini untuk les olimpiade matematika
Contoh Soal Persamaan Lingkaran
Mari kita lihat beberapa contoh soal persamaan lingkaran dan jawabannya untuk lebih memahami materi ini.
Contoh Soal 1: Tentukan Persamaan Lingkaran
Soalnya:
Tentukan persamaan lingkaran dengan pusat 0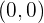 
dan berjari-jari 
.
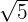Penyelesaian:
Untuk lingkaran yang berpusat di 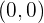dengan jari-jari 
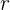, persamaan bakunya adalah:
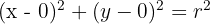
Substitusi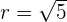 
:
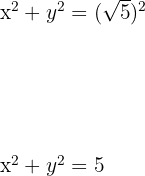
Jadi, persamaan lingkaran adalah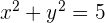 
.
Contoh Soal 2: Bentuk Umum Persamaan Lingkaran
Soalnya:
Misalkan kita diberikan persamaan lingkaran dalam bentuk umum, yaitu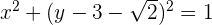 
. Tentukan persamaan lingkaran dalam bentuk umum.
Penyelesaian:
Kita mulai dengan menyederhanakan persamaan tersebut:
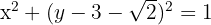
Expansi:
Cek di sini les matematika online
Contoh Soal 3: Menentukan Persamaan Lingkaran dari Titik dan Jari-jari
Soalnya:
Tentukan persamaan lingkaran yang berpusat di titik 
dan jari-jari lingkaran adalah 4.
Penyelesaian:
Gunakan formula baku persamaan lingkaran:
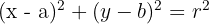
Substitusi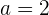 
, 
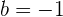, dan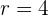 
:
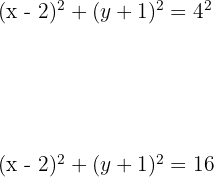
Jadi, persamaan lingkaran adalah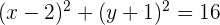 
.
Itulah beberapa contoh soal lingkaran kelas 11 beserta jawabannya, semoga dapat membantu!
Ini adalah rumus peluang yang wajib Anda pahami!
Latihan Soal!
Jika titik (-5,k) terletak pada lingkaran x2 + y2 + 2x – 5y – 21 = 0, berapakah nilai k?
Diskusikan jawaban Anda pada kolom komentar!
Perpotongan Garis dan Lingkaran
Selain menentukan persamaan lingkaran, pada materi lingkaran kelas 11, Anda juga akan belajar bagaimana memperhitungkan apakah suatu garis h yang memiliki persamaan y = mx + n tersebut tidak menyentuh, menyinggung, atau memotong suatu lingkaran yang memiliki persamaan x2 + y2 + Ax + By + C = 0, dengan menggunakan prinsip diskriminan.
Diskriminan (D = b2 – 4ac) diambil dari persamaan kuadrat yang merupakan hasil substitusi dari persamaan garis dengan persamaan lingkarannya, dan dapat dilihat kedudukan garis lurus terhadap lingkaran, sebagai berikut;
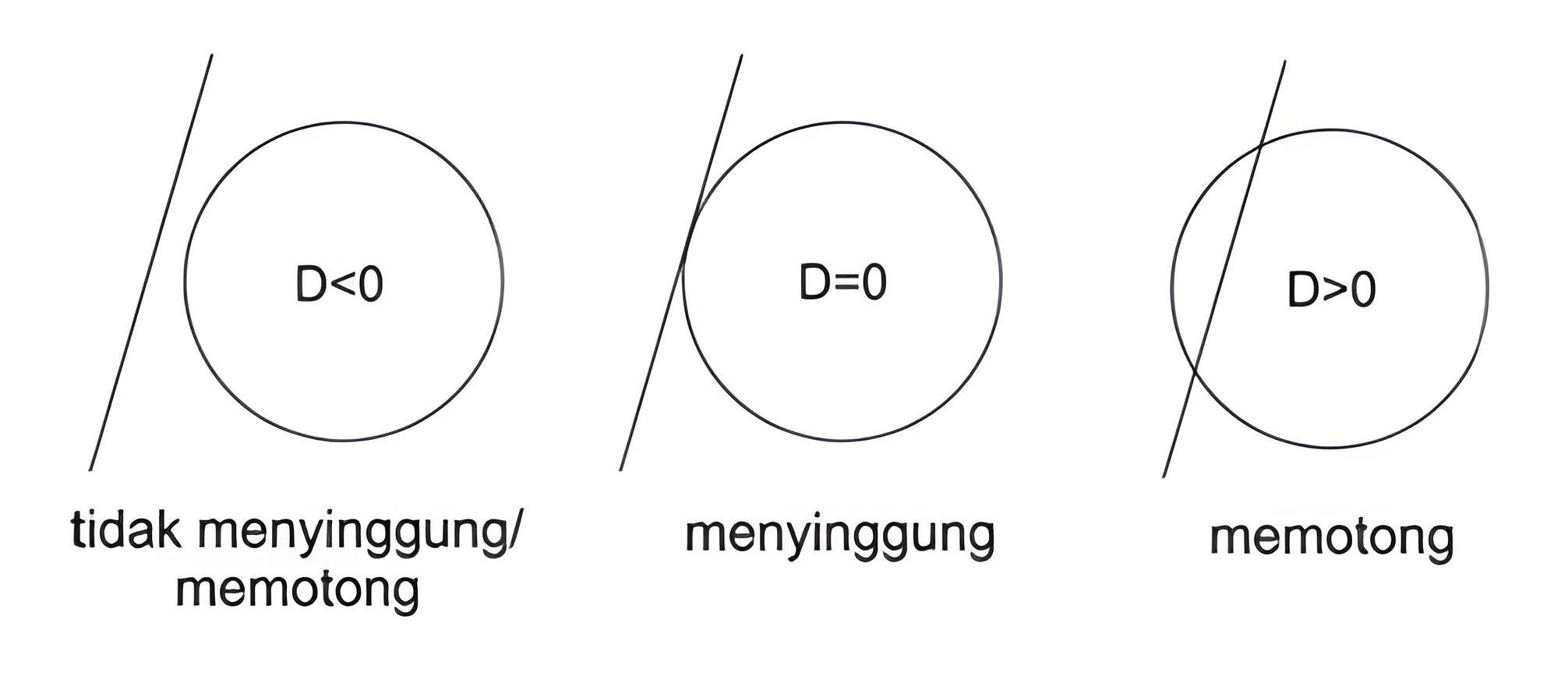
Keterangan;
- Garis h tidak memotong atau menyinggung lingkaran, jika D < 0
- Garis h menyinggung lingkaran, jika D = 0
- Garis h memotong lingkaran, jika D > 0
Periksa di sini jika sedang mencari les matematika online
Pengaruh Perubahan Titik Pusat terhadap Kedudukan Lingkaran
Saat titik pusat lingkaran berpindah, posisi seluruh lingkaran dalam bidang koordinat ikut berubah. Oleh karena itu, memahami cara menghitung rumus titik pusat sangat penting dalam konteks perubahan posisi lingkaran. Perpindahan titik pusat dapat mengubah kedudukan lingkaran relatif terhadap lingkaran lain atau garis yang ada, yang tentunya mempengaruhi bagaimana dua lingkaran berinteraksi satu sama lain.
Kedudukan Lingkaran dalam Geometri Analitik
Lingkaran adalah bangun datar yang memiliki banyak aplikasi dalam geometri analitik. Salah satu konsep penting yang perlu dipahami adalah kedudukan lingkaran, yang berkaitan dengan hubungan dua lingkaran atau garis dan lingkaran dalam suatu sistem koordinat. Dengan memahami kedudukan lingkaran, kita dapat menentukan apakah dua lingkaran berpotongan, bersinggungan, atau tidak berpotongan sama sekali.
Dalam geometri analitik, kedudukan lingkaran terhadap lingkaran sangat penting untuk memahami hubungan antara dua lingkaran. Ini mencakup tiga jenis kedudukan: berpotongan, bersinggungan luar, dan bersinggungan dalam.
Kedudukan Garis terhadap Lingkaran
Selain itu, dalam materi ini juga dibahas tentang kedudukan lingkaran terhadap suatu garis. Dengan menggunakan diskriminan dari persamaan kuadrat, kita bisa mengetahui apakah garis tersebut menyentuh, memotong, atau tidak memiliki titik potong sama sekali dengan lingkaran. Ini adalah bagian penting dalam memahami persamaan lingkaran secara lebih mendalam.
Kedudukan Dua Lingkaran
Memahami kedudukan relatif antara dua lingkaran sangat penting karena membantu kita menentukan bagaimana dua lingkaran berinteraksi satu sama lain dalam bidang koordinat. Kedudukan 2 lingkaran dapat digolongkan ke dalam beberapa kategori berdasarkan jarak antara pusat-pusat lingkaran dan jari-jari masing-masing lingkaran. Mari kita jelajahi lebih dalam tentang kategori-kategori ini dan cara menghitung kedudukan dua lingkaran.
Jenis-Jenis Kedudukan Dua Lingkaran
a. Dua Lingkaran Berpotongan
Dua lingkaran berpotongan jika mereka memiliki dua titik potong. Kondisi ini terjadi ketika jarak antara pusat kedua lingkaran lebih kecil dari jumlah jari-jari mereka tetapi lebih besar dari selisih jari-jari mereka.
Secara matematis, jika kita memiliki dua lingkaran:
- Lingkaran 1 dengan pusat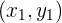 
dan jari-jari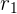 
- Lingkaran 2 dengan pusat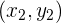 
dan jari-jari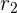 
Jarak antara pusat kedua lingkaran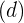 
dapat dihitung dengan rumus:
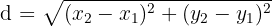
Kedua lingkaran berpotongan jika:
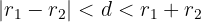
b. Dua Lingkaran Bersinggungan
Dua lingkaran bersinggungan jika mereka memiliki satu titik potong. Ada dua jenis bersinggungan:
- Bersinggungan Luar (Eksternal):
Dua lingkaran bersinggungan luar jika jarak antara pusat kedua lingkaran sama dengan jumlah dari jari-jari keduanya.
- Bersinggungan Dalam (Internal):
Dua lingkaran bersinggungan dalam jika jarak antara pusat kedua lingkaran sama dengan selisih dari jari-jari keduanya.
c. Dua Lingkaran Tidak Berpotongan
Dua lingkaran tidak berpotongan jika mereka tidak memiliki titik potong sama sekali. Ada dua kasus di mana hal ini terjadi:
- Tidak Berpotongan dan Tidak Bersinggungan:
Ini terjadi jika jarak antara pusat lebih besar dari jumlah jari-jari.
d > r1 + r2
- Tidak Berpotongan dan Tidak Bersinggungan (terpisah secara internal):
Ini terjadi jika jarak antara pusat lebih kecil dari selisih jari-jari.
d < | r1 - r2 |
d. Dua lingkaran berpotongan tegak lurus (Orthogonal)
Kedua lingkaran dikatakan berpotongan tegak lurus apabila memenuhi kondisi bahwa kuadrat jarak antara pusat kedua lingkaran 
sama dengan jumlah kuadrat dari jari-jarinya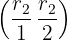 
.
Dua Lingkaran Orthogonal: (P1P2)2 =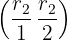
e. Lingkaran L2 memotong dan membagi dua sama besar lingkaran L1
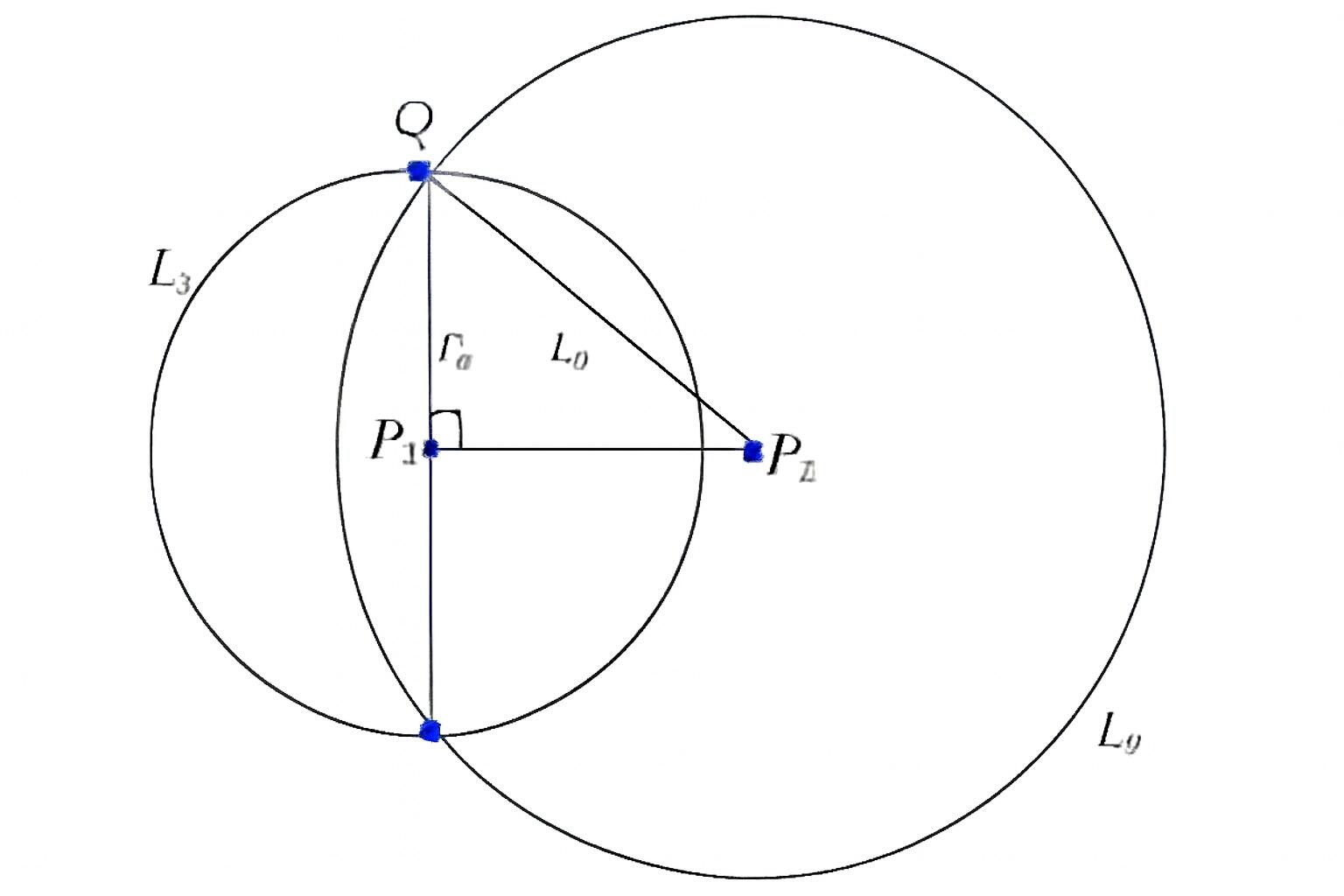
Pada gambar di atas telah ditunjukkan bahwa lingkaran L2 membagi lingkaran L1 menjadi dua bagian yang sama besar. Situasi ini terjadi ketika syarat kuadrat jarak antara pusat kedua lingkaran 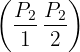sama dengan selisih kuadrat jari-jarinya 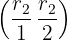terpenuhi.
Lingkaran L2 memotong dan membagi dua sama besar lingkaran L1 : (P1P2)2 =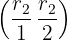
Langkah-Langkah Menentukan Kedudukan Dua Lingkaran
Untuk menentukan kedudukan dua lingkaran, ikuti langkah-langkah berikut:
1. Tentukan Pusat dan Jari-Jari Lingkaran:
Ekspresikan persamaan lingkaran dalam bentuk baku untuk mengidentifikasi pusat 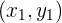dan jari-jari 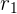dari lingkaran pertama dan pusat 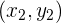serta jari-jari 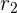dari lingkaran kedua.
2. Hitung Jarak Antara Pusat:
Gunakan rumus jarak antara dua titik:
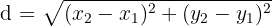
3. Bandingkan Jarak dengan Jari-Jari:
- Jika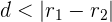 
, lingkaran tidak berpotongan dan terpisah secara internal.
- Jika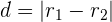 
, lingkaran bersinggungan dalam.
- Jika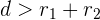 
, lingkaran tidak berpotongan dan terpisah.
- Jika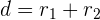 
, lingkaran bersinggungan luar.
- Jika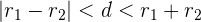 
, lingkaran berpotongan di dua titik.
Contoh Perhitungan Kedudukan Dua Lingkaran
Contoh 1: Dua Lingkaran Berpotongan
Misalkan kita memiliki dua lingkaran:
- Lingkaran A dengan pusat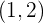 
dan jari-jari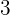 
- Lingkaran B dengan pusat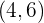 
dan jari-jari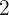 
Pertama, hitung jarak antara pusat kedua lingkaran:
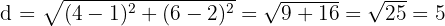
Kemudian, cek kondisi:
| 3 - 2 | = 1 dan 3 + 2 = 5
1 < 5 < 5
Karena jarak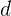 
berada di antara selisih dan jumlah jari-jari, kedua lingkaran berpotongan di dua titik.
Contoh 2: Dua Lingkaran Bersinggungan Luar
Misalkan kita memiliki dua lingkaran:
- Lingkaran C dengan pusat 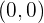dan jari-jari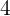 
- Lingkaran D dengan pusat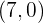 
dan jari-jari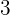
Hitung jarak antara pusat kedua lingkaran:
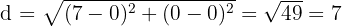
Kemudian, cek kondisi:
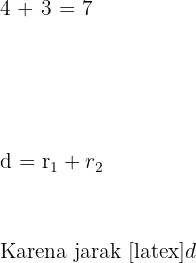Karena jarak sama dengan jumlah jari-jari, kedua lingkaran bersinggungan luar.
Contoh 3: Dua Lingkaran Tidak Berpotongan
Misalkan kita memiliki dua lingkaran:
- Lingkaran E dengan pusat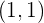 
dan jari-jari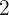
- Lingkaran F dengan pusat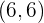 
dan jari-jari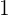 
Hitung jarak antara pusat kedua lingkaran:
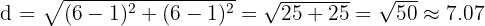
Kemudian, cek kondisi:
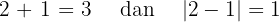
7.07 > 3 dan 7.07 > 1
Karena jarak 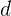lebih besar dari jumlah jari-jari dan juga lebih besar dari selisih jari-jari, kedua lingkaran tidak berpotongan dan tidak bersinggungan.
Kesimpulan :
- Pengertian dan Rumus Titik Pusat Lingkaran
Lingkaran adalah sekumpulan titik dengan jarak sama terhadap titik pusat. Rumus titik pusat digunakan untuk menentukan posisi pusat lingkaran dalam koordinat kartesius, yang sangat penting dalam menggambarkan dan menganalisis lingkaran. - Persamaan Lingkaran dan Kedudukan Lingkaran
Persamaan lingkaran menggambarkan hubungan antara titik-titik keliling lingkaran dan pusatnya. Kedudukan lingkaran, baik terhadap garis maupun lingkaran lain, ditentukan berdasarkan jarak antara pusat dan jari-jari masing-masing. - Aplikasi dan Simetri Lingkaran
Titik pusat memainkan peran kunci dalam aplikasi dunia nyata, seperti dalam desain teknis, perhitungan jarak, dan analisis data spasial. Lingkaran memiliki simetri lipat tak terhingga, dengan titik pusat sebagai acuan utama, yang juga digunakan dalam menghitung luas dan keliling lingkaran.
Dengan pemahaman ini, kita dapat lebih mudah menyelesaikan berbagai permasalahan terkait lingkaran dalam matematika dan aplikasinya di berbagai bidang.
Jika Anda ingin menguasai matematika dan mencapai pemahaman yang lebih dalam, saatnya mencari guru privat di Superprof!
Dapatkan bimbingan langsung dari pengajar berpengalaman yang akan membantu Anda menguasai konsep-konsep sulit dengan lebih mudah. Jangan lewatkan kesempatan untuk meningkatkan keterampilan matematika dan meraih hasil belajar maksimal. Kunjungi Superprof hari ini dan temukan guru privat yang tepat untuk membantu Anda meraih tujuan akademis dengan cara yang menyenangkan dan efektif!
Apakah Anda pernah mendengar tentang matriks matematika? jika belum, klik artikel Kami untuk mempelajarinya!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
Ringkasan yang bagus, mudah dipahami
Terima kasih atas apresiasi nya, semoga bermanfaat ya :)
Alhamdulillah sedikit bisa di mengerti
Alhamdulillah
Belajar matematika sangat menyenangkan
Keren
matapp pakkk…
makasih :)
Terima kasih sudah berbagi Pak. Terus berkarya dan berbagi
Sama2, semoga bermanfaat ya, kata2 dari kamu bikin jadi tambah semangat :)