Pada materi bangun ruang, ada dua rumus utama yang perlu dipelajari, yaitu perhitungan volume dan luas permukaan. Kedua rumus ini sangat penting digunakan untuk menentukan ukuran berbagai bentuk bangun tiga dimensi.
Beberapa contoh bangun ruang yang sering dipelajari yaitu kubus, balok, prisma, tabung, limas, kerucut, dan bola. Lewat artikel ini, kita akan ajak kamu mempelajari rumus bangun ruang, dilengkapi contoh soal bangun ruang!

Pengertian Bangun Ruang

Bangun ruang merupakan objek geometri tiga dimensi, yaitu panjang, lebar, dan tinggi.
Inilah yang membuat bangun ruang jadi punya sisi beda dengan bangun datar yang hanya dua dimensi.
Karena memiliki tiga ukuran, bangun ruang juga sering disebut sebagai bentuk tiga dimensi atau 3D. Bangun datar termasuk bentuk dua dimensi atau 2D.Dalam pembahasan bangun ruang, ada dua konsep utama, yaitu volume dan luas permukaan.
Volume bangun ruang menunjukkan seberapa besar ruang yang dapat diisi oleh benda.
Contohnya, botol minum biasanya punya kapasitas seperti 500 ml atau 1 liter. Angka tersebut menunjukkan volume maksimum yang bisa ditampung oleh botol tersebut.
Bangun ruang juga punya luas permukaan. Luas permukaan bangun ruang merupakan total luas seluruh sisi luar bangun dan sering digunakan saat membuat jaring-jaring bangun ruang.
Rumus Volume dan Luas Permukaan
Pada umumnya, rumus volume bangun ruang diperoleh dengan mengalikan luas alas dengan tinggi bangun. Namun, untuk bangun ruang yang memiliki puncak seperti limas dan kerucut, hasil tersebut dibagi tiga.
Sementara itu, rumus luas permukaan bangun ruang dihitung dengan menjumlahkan luas seluruh sisi yang membentuk bangun tersebut. Luas permukaan menggunakan satuan persegi, seperti cm². Agar lebih paham, kamu bisa latihan lewat les matematika dengan tutor berpengalaman.
Berikut penjelasan rumus rumus bangun ruang lebih rincinya.
1. Kubus

Kubus merupakan bangun ruang sisi datar yang memiliki enam sisi berbentuk persegi dengan panjang rusuk yang sama. Semua sisinya memiliki ukuran yang identik.
Volume kubus dihitung dengan mengalikan panjang rusuk sebanyak tiga kali. Oleh karena itu, rumus volume bangun ruang kubus dituliskan sebagai:
V = s × s × s atau V = s³
Sementara itu, rumus luas permukaan kubus diperoleh dengan menjumlahkan luas keenam sisinya. Rumusnya adalah:
L = 6 × (s × s)
Contoh Soal
Sebuah kubus memiliki panjang sisi sebesar 8 cm. Tentukan:
Sebuah kubus memiliki panjang sisi 8 cm.
a. Volume Kubus
V = s³
V = 8³
V = 512 cm³
b. Luas Permukaan Kubus
L = 6 × s²
L = 6 × 64
L = 384 cm²
Luas Permukaan KubusL = 6 × s²L = 6 × 64L = 384 cm²Dengan demikian, luas permukaan kubus tersebut adalah 384 cm².
2. Balok

Balok adalah bangun ruang yang bentuknya hampir sama dengan kubus, tetapi ukuran sisinya tidak selalu sama. Semua sisi balok berbentuk persegi panjang.
Rumus volume bangun ruang balok dihitung dengan mengalikan panjang, lebar, dan tinggi, yaitu:
V = p × l × t
Adapun luas permukaan balok diperoleh dengan menjumlahkan luas seluruh sisi yang Sementara itu, rumus luas permukaan balok diperoleh dari penjumlahan luas seluruh sisinya:
L = 2 × [(p × l) + (p × t) + (l × t)]
Contoh Soal
Balok memiliki panjang 12 cm, lebar 8 cm, dan tinggi 5 cm.
a. Volume Balok
V = 12 × 8 × 5
V = 480 cm³
b. Luas Permukaan Balok
L = 2 × (96 + 60 + 40)
L = 392 cm²
Dengan demikian, luas permukaan balok tersebut adalah 392 cm².
3. Limas
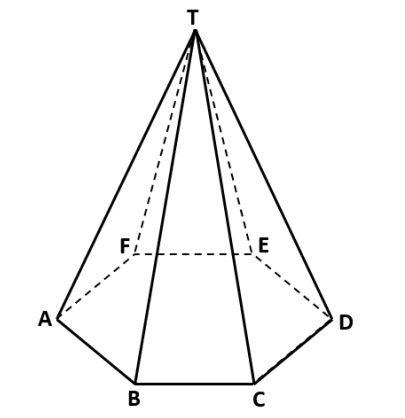
Limas merupakan bangun ruang sisi datar yang memiliki satu alas berbentuk poligon dan sisi-sisi tegak berbentuk segitiga. Semua sisi tegak bertemu pada satu titik puncak. Nama limas ditentukan berdasarkan bentuk alasnya, seperti limas segitiga atau limas segiempat.
Rumus Luas Permukaan Limas adalah:
L = L alas + L selimut
Sedangkan rumus volume bangun ruang limas adalah:
V = ⅓ × L alas × t
Contoh Soal
Limas dengan alas persegi memiliki sisi 5 cm dan tinggi 10 cm.
Luas alas = 25 cm²
Volume = ⅓ × 25 × 10 = 83,33 cm³
Dengan demikian, volume limas persegi tersebut adalah 83,33 cm³.
4. Prisma
Prisma adalah bangun ruang yang memiliki dua alas sejajar dan sama bentuk. Sisi-sisi tegaknya berbentuk persegi panjang.
Rumus volume bangun ruang prisma adalah:
V = L alas × t
Sementara itu, rumus luas permukaan prisma adalah:
L = (2 × L alas) + (K alas × t)
Rumus Volume Prisma
Volume prisma dihitung dengan mengalikan luas alas dengan tinggi prisma.
Rumus umum volume prisma adalah:
V = L alas × t
Contoh Soal 1
Sebuah prisma segitiga siku-siku memiliki sisi alas sepanjang 3 cm, 4 cm, dan 5 cm. Jika tinggi prisma adalah 6 cm, tentukan luas permukaan prisma tersebut.
Penyelesaian
Rumus luas permukaan prisma:
L = (2 × L alas) + (K alas × t)
Luas alas
Karena alas berbentuk segitiga siku-siku, maka:
L alas = ½ × alas × tinggi
L alas = ½ × 3 × 4 = 6 cm²
Keliling alas
K alas = 3 + 4 + 5 = 12 cm
Luas permukaan prisma
L = (2 × 6) + (12 × 6)
L = 12 + 72
L = 84 cm²
Jadi, luas permukaan prisma segitiga tersebut adalah 84 cm².
Contoh Soal 2
Diketahui sebuah prisma segitiga memiliki luas alas sebesar 20 cm² dan tinggi prisma 12 cm. Tentukan volume prisma tersebut.
Penyelesaian
Rumus volume prisma:
V = L alas × t
V = 20 × 12
V = 240 cm³
Dengan demikian, volume prisma segitiga tersebut adalah 240 cm³.
5. Bola
BolaBola merupakan bangun ruang yang seluruh permukaannya melengkung dan memiliki jarak yang sama ke titik pusat. Bola tidak memiliki rusuk maupun titik sudut.
Rumus luas permukaan bangun ruang bola adalah:
L = 4 × π × r²
Sedangkan rumus volume bangun ruang bola adalah:
V = 4/3 × π × r³
Catatan
Nilai π dapat digunakan 22/7 atau 3,14, menyesuaikan dengan data yang tersedia dalam soal.
Contoh Soal
Sebuah bola memiliki jari-jari 10 cm. Tentukan:
a. Luas permukaan bola
b. Volume bola
Penyelesaian
a. Luas Permukaan Bola
Rumus:
L = 4 × π × r²
Diketahui:
r = 10 cm, gunakan π = 3,14
Perhitungan:
L = 4 × 3,14 × 10²
L = 4 × 3,14 × 100
L = 1.256 cm²
Jadi, luas permukaan bola tersebut adalah 1.256 cm².
b. Volume Bola
Rumus:
V = 4/3 × π × r³
Perhitungan:
V = 4/3 × 3,14 × 10³
V = 4/3 × 3,14 × 1.000
V = 4.186,67 cm³
Dengan demikian, volume bola tersebut adalah 4.186,67 cm³.
6. Kerucut
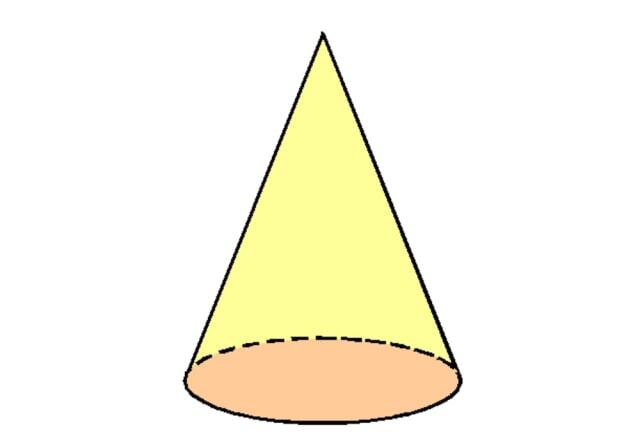
Kerucut memiliki satu alas berbentuk lingkaran dan satu titik puncak. Kerucut termasuk bangun ruang yang memiliki sisi lengkung.
Rumus luas permukaan kerucut adalah:
L = π × r × (r + s)
Rumus volume bangun ruang kerucut adalah:
V = ⅓ × π × r² × t
Garis pelukis kerucut dapat dihitung dengan rumus:
s = √(r² + t²)
Contoh Soal
Sebuah kerucut memiliki jari-jari alas 7 cm dan tinggi 24 cm. Tentukan:
a. Garis pelukis kerucut
b. Luas permukaan kerucut
c. Volume kerucut
Penyelesaian
Diketahui:
r = 7 cm
t = 24 cm
π = 22/7
a. Garis Pelukis Kerucut
Rumus:
s = √(r² + t²)
s = √(7² + 24²)
s = √(49 + 576)
s = √625
s = 25 cm
b. Luas Permukaan Kerucut
Rumus:
L = π × r × (r + s)
L = 22/7 × 7 × (7 + 25)
L = 22 × 32
L = 704 cm²
c. Volume Kerucut
Rumus:
V = ⅓ × π × r² × t
V = ⅓ × 22/7 × 7² × 24
V = ⅓ × 22 × 7 × 24
V = ⅓ × 3.696
V = 1.232 cm³
Jadi:
- Garis pelukis kerucut = 25 cm
- Luas permukaan kerucut = 704 cm²
- Volume kerucut = 1.232 cm³
7. Tabung
Tabung merupakan bangun ruang yang memiliki dua alas berbentuk lingkaran dan satu sisi lengkung. Jika sisi lengkungnya dibentangkan, bentuknya menyerupai persegi panjang.
Rumus volume bangun ruang tabung adalah:
V = π × r² × t
Sedangkan rumus luas permukaan bangun ruang tabung adalah:
L = 2 × π × r × (r + t)
Sebagai kesimpulan, bangun ruang adalah materi dasar matematika yang sangat penting untuk dikuasai karena mencakup rumus bangun ruang, volume dan luas permukaan bangun ruang bangun ruang yang sering muncul dalam soal. Dengan mempelajari rumus bangun datar dan bangun ruang seperti rumus volume, luas permukaan bangun ruang dan rajin mengerjakan contoh soal bangun ruang. Proses belajar lebih mudah. Untuk pendampingan belajar lebih jauh, join langsung di kelas privat matematika Superprof! Di Superprof, kamu bisa pilih tutor matematika berpengalaman dan belajar via les matematika online dimanapun. Kamu juga bisa belajar mean median modus.
Ringkaskan dengan AI















