Statistika sebenarnya adalah ilmu yang membantu kita memahami data dengan cara yang lebih masuk akal. Ilmu ini membahas bagaimana data dikumpulkan, diolah, dianalisis, sampai akhirnya bisa ditarik kesimpulan yang benar dan bisa dipertanggungjawabkan.
Dalam kehidupan sehari-hari, statistika sering banget dipakai tanpa kita sadari. Misalnya saat membandingkan nilai ujian dengan rata-rata kelas, atau ketika pemerintah melakukan sensus penduduk untuk melihat kondisi masyarakat secara keseluruhan. Dari sini bisa kelihatan kalau statistika punya peran penting dalam pengambilan keputusan berbasis angka.
Mean (Rata-Rata)
Mean adalah istilah lain dari rata-rata yang sudah sering kita dengar sejak sekolah dasar.
Mean digunakan untuk mewakili sekumpulan data dalam satu nilai yang dianggap bisa menggambarkan kondisi umum data tersebut.
Cara mendapatkan mean cukup sederhana, yaitu dengan menjumlahkan seluruh data lalu membaginya dengan jumlah data yang ada. Dalam penulisan matematika, mean biasanya dilambangkan dengan simbol x̄ yang dibaca “x bar”.
Perhitungan mean bisa diterapkan pada data tunggal maupun data berkelompok. Perbedaannya terletak pada cara data tersebut disajikan, apakah masih berupa angka mentah atau sudah dikelompokkan dalam tabel tertentu.
Data tunggal sendiri adalah data yang diperoleh secara langsung tanpa melalui proses pengelompokan. Data ini bisa disusun secara acak atau berurutan, sehingga perhitungan mean-nya bisa dilakukan secara langsung.
Median (Nilai Tengah)
Median adalah nilai yang berada tepat di tengah suatu kumpulan data setelah data tersebut diurutkan dari yang paling kecil sampai yang paling besar.
Median berfungsi sebagai pembatas antara setengah data di bawah dan setengah data di atasnya.
Median biasanya dilambangkan dengan simbol Me. Ukuran ini sering digunakan karena tidak terlalu terpengaruh oleh nilai yang terlalu besar atau terlalu kecil dalam data.Cara menentukan median sangat bergantung pada jumlah data yang dimiliki.
Kalau jumlah datanya ganjil, median bisa langsung diambil dari nilai tengah, sedangkan kalau jumlah datanya genap, median diperoleh dari rata-rata dua nilai yang berada di tengah.
Modus (Nilai yang Paling Sering Muncul)
Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Dengan kata lain, modus menunjukkan nilai yang paling dominan dibandingkan nilai lainnya.
Dalam statistika, modus biasanya dilambangkan dengan simbol Mo. Sebuah data bisa saja memiliki satu modus, lebih dari satu modus, atau bahkan tidak memiliki modus sama sekali.
Pada data yang sudah disajikan dalam tabel frekuensi atau data berkelompok, modus dapat ditentukan dengan melihat nilai yang memiliki frekuensi paling besar. Sedangkan, penyusunan tabel turus di data tunggal membantu kamu untuk melihat frekuensi setiap nilai dengan lebih jelas.
Rumus Mean Data Tunggal
Cara menghitung mean data tunggal dihitung dengan menjumlahkan seluruh nilai data yang sudah disediakan, lalu lanjut dibagi dengan jumlah data tersebut.
Data tunggal merupakan data yang belum dikelompokkan dan belum di utak-atik. Rumus cara mencari mean :
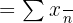
Keterangan:
- (\bar{x}) = mean (rata-rata)
- (\sum x) = jumlah seluruh nilai data
- (n) = banyaknya data
Dimulai dari menuliskan seluruh data, lalu dijumlahkan dengan semua nilai. Hasil penjumlahan dibagi dengan jumlah data untuk mendapatkan hasil nilai mean.
Rumus Mean Data Kelompok
Kalau jumlah data sudah terlalu banyak, maka data tidak ditulis satu per satu lagi. Supaya lebih rapi dan mudah dibaca, data tersebut akan dikelompokkan ke dalam beberapa kelas yang disebut dengan mean data kelompok.
Berbeda dengan mean data tunggal. Karena itulah, perhitungan rumus mean dilakukan dengan bantuan nilai tengah kelas yang dianggap mewakili seluruh data dalam kelas.
Berikut rumus mean data kelompok:
(x_i) = nilai tengah kelas
(f) = frekuensi dari masing-masing kelas
(\sum f) = jumlah seluruh data yang ada.
Langkah pertama yang perlu dilakukan adalah menentukan nilai tengah dari setiap kelas interval. Setelah itu, nilai tengah dikalikan dengan frekuensinya masing-masing agar memperoleh gambaran kontribusi tiap kelas terhadap rata-rata.
Langkah selanjutnya yaitu menjumlahkan seluruh hasil perkalian antara nilai tengah dan frekuensi. Terakhir, hasil penjumlahan dibagi dengan jumlah seluruh frekuensi untuk mendapat nilai mean data kelompok.
Meski terlihat sedikit lebih panjang dibanding data tunggal, cara menghitung mean data kelompok tetap logis dan mudah dipahami. Selama langkah-langkahnya dilakukan urut, maka hasil mean yang diperoleh dapat mewakili keseluruhan data dengan tepat.
Contoh Soal Mean
Diketahui data nilai ulangan matematika dari 8 siswa, yaitu 70, 75, 80, 85, 90, 75, 80, dan 85.
Jumlah data yang tersedia adalah 8. Mean dihitung dengan rumus :
70 + 75 + 80 + 85 + 90 + 75 + 80 + 85 = 640
Jumlah data yang tersedia adalah 8, sehingga mean dapat dihitung dengan rumus:
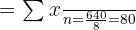
Nilai mean digunakan mewakili rata-rata nilai ulangan siswa dalam kelas.
Rumus Median
Sebelum menentukan cara menghitung median, hal paling penting yang harus dilakukan adalah mengurutkan data dari nilai terkecil sampai nilai terbesar. Jika jumlah data ganjil, maka median diambil dari nilai yang ada di tengah (rumus median data tunggal).
Sebaliknya, jika jumlah data genap, maka ada dua nilai tengah, median bisa diperoleh dari rata-rata kedua nilai. Untuk mempermudah perhitungan, median biasanya ditentukan menggunakan rumus median sesuai dengan jumlah data yang dimiliki.
Cara Mencari Median
- Median untuk Data Berjumlah Ganjil
Median untuk Data Berjumlah GanjilJika jumlah data (n) bersifat ganjil, maka median ditentukan dengan rumus: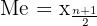
Rumus ini menunjukkan bahwa median berada pada posisi tengah susunan data. - Median untuk Data Berjumlah Genap
Median untuk Data Berjumlah GenapJika jumlah data (n) bersifat genap, maka median ditentukan dengan: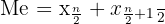
Rumus ini digunakan untuk mendapatkan nilai tengah yang paling representatif.
Contoh Soal Median
Soal 1 (Data Berjumlah Ganjil)
Diketahui data sebagai berikut:
5, 7, 9, 11, 13
Tentukan median dari data tersebut.
Penyelesaian:
Data sudah tersusun berurutan dan jumlah data ( n = 5 ) (ganjil).
Posisi median ditentukan dengan rumus: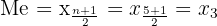
Nilai data ke-3 adalah 9.
Kesimpulan:
Median dari data tersebut adalah 9.
Soal 2 (Data Berjumlah Genap)
Diketahui data sebagai berikut:
4, 6, 8, 10, 12, 14
Tentukan median dari data tersebut.
Penyelesaian:
Data sudah tersusun berurutan dan jumlah data ( n = 6 ) (genap).
Median dihitung dengan rumus: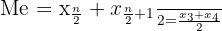
Nilai data ke-3 adalah 8 dan data ke-4 adalah 10, sehingga: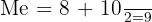
Kesimpulan:
Median dari data tersebut adalah 9.
Rumus Modus
Pada data tunggal, modus tidak punya rumus matematika khusus seperti mean dan median. Modus ditentukan dengan cara melihat nilai yang paling sering muncul dalam kumpulan data.
Secara umum, cara menghitung modus dinyatakan sebagai nilai data dengan jumlah terbesar.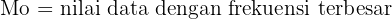
Contoh Soal Modus (Data Tunggal)
Diketahui data 6, 7, 8, 7, 9, 7, 8, dan 10. Cara mencari modus, langkah pertama yang perlu dilakukan yaitu menghitung frekuensi setiap nilai.
Tentukan modus dari data tersebut.
Penyelesaian:
Hitung frekuensi masing-masing nilai:
- 6 muncul 1 kali
- 7 muncul 3 kali
- 8 muncul 2 kali
- 9 muncul 1 kali
- 10 muncul 1 kali
Nilai dengan frekuensi terbanyak adalah 7.
Rumus Mean, rumus median, dan rumus modus bukan sekadar rumus yang wajib dihafal saat mau ujian. Ketiganya membantu kamu dalam memahami data dengan cara yang lebih masuk akal, mulai dari melihat nilai rata-rata kelas, menentukan nilai tengah, sampai mengetahui nilai yang paling sering muncul. Kalau konsep dasarnya sudah dipahami, statistika justru terasa lebih ringan, logis, dan nggak lagi menakutkan.
Kalau kamu masih sering merasa “nyangkut” saat belajar statistika atau pengin penjelasan yang lebih santai dan sesuai gaya belajarmu, belajar bareng tutor privat bisa jadi pilihan yang tepat. Lewat Superprof, kamu bisa menemukan guru privat yang siap membantu memahami rumus mean median modus dengan cara yang lebih personal dan mudah dipahami. Yuk, mulai belajar dengan cara yang lebih nyaman dan bikin statistika jadi lebih bersahabat!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
