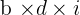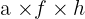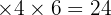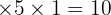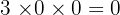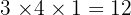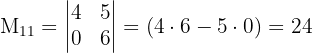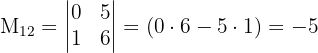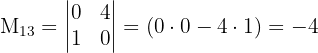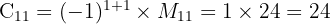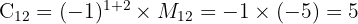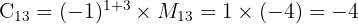Dalam matematika, matriks adalah salah satu materi yang perlu Anda pelajari karena manfaatnya yang penting, salah satunya dalam bidang informatika. Yap, benar sekali. Materi matriks matematika digunakan dalam sistem komputer, misalnya pada bidang keamanan komputer dan pemrograman yang memerlukan array dalam penerapannya. Selain itu, enkripsi data dalam Ilmu Komputer juga dapat dilakukan menggunakan berbagai operasi matriks.
Karena kegunaannya yang luar biasa ini, hari ini kita akan membahas cara menentukan determinan matriks dengan berbagai cara, mulai dari determinan matriks 2x2, 3x3 dengan aturan Sarrus, 3x3 metode minor kofaktor, hingga rumus invers matriks. Dan tentu saja kita juga akan mempelajari contoh soal serta pembahasannya di akhir artikel. Yuk, simak sampai selesai ya!
Cek di sini untuk les matematika online
Apa Itu Matriks?
Matrix adalah susunan bilangan real atau bilangan kompleks (atau elemen-elemen) yang disusun dalam baris dan kolom sehingga membentuk jajaran persegi panjang. Dengan kata lain, matriks itu seperti kotak yang penuh angka, yang tersusun rapi dalam kolom dan baris. Biasanya, matriks digunakan dalam berbagai cabang matematika, terutama dalam aljabar linier, untuk memecahkan sistem persamaan linear, transformasi ruang, hingga aplikasi lainnya dalam ilmu komputer dan teknik.
Jadi, kalau kamu melihat sebuah kumpulan angka yang terorganisir rapi dalam format baris dan kolom, sudah bisa dipastikan itu adalah matriks! Keren, kan?
Ordo Matriks
Ordo matriks adalah jumlah baris dan kolom dalam matriks tersebut. Misalnya, sebuah matriks berordo 2x3 berarti matriks tersebut memiliki 2 baris dan 3 kolom. Untuk menentukan ordo matriks, cukup hitung saja berapa banyak baris dan kolom yang ada. Jadi, kalau ada yang tanya "Ordo matriks itu apa?" jawabannya gampang banget: "Itu lho, jumlah baris dan kolomnya!"
Jenis Jenis Matriks
Ada beberapa jenis matriks yang perlu kamu ketahui, dan setiap jenis matriks memiliki karakteristik uniknya sendiri. Berikut adalah jenis jenis matriks yang perlu kamu ketahui:
- Matriks Nol: Matriks yang seluruh elemennya adalah bilangan nol. Contoh:
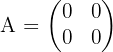
- Matriks Baris: Matriks yang hanya memiliki satu baris, berordo 1 x j. Contoh:
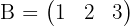
- Matriks Kolom: Matriks yang hanya memiliki satu kolom, berordo i x 1. Contoh:
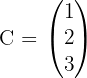
- Matriks Persegi: Matriks yang banyaknya baris sama dengan banyaknya kolom, berordo i x i. Contoh:
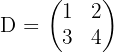
- Matriks Diagonal: Matriks persegi yang semua elemennya nol, kecuali pada diagonal utamanya. Contoh:
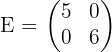
- Matriks Identitas: Matriks persegi yang elemen pada diagonal utamanya adalah satu, sedangkan elemen lainnya adalah nol. Contoh:
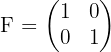
Dalam kasus invers matriks, kita hanya bisa menghitung determinan dan invers , yaitu matriks yang memiliki jumlah baris dan kolom yang sama, misalnya matriks 2x2, 3x3, dan seterusnya.
Determinan Matriks
Setelah memahami apa itu matriks dan jenis-jenis matriks, mari kita masuk ke salah satu topik penting, yaitu determinan. Apa itu determinan matriks? Secara sederhana, determinan adalah suatu nilai yang dihasilkan dari matriks persegi yang menggambarkan "ukurannya". Dalam kata lain, determinan matriks memberi tahu kita seberapa besar atau kecil pengaruh matriks tersebut dalam suatu sistem. Jika nilai determinannya adalah nol, itu menandakan bahwa matriks tersebut tidak dapat dibalik (singular).
Jika Anda ingin memahami pengertian logika matematika, silahkan baca artikel kami lainnya!
Rumus Determinan Matriks
Nah, sekarang mari kita bahas beberapa rumus determinan yang wajib kamu tahu, dimulai dari matriks 2x2 dan 3x3.
1. Rumus Determinan Matriks 2x2
Untuk matriks berordo 2x2, rumus determinannya sangat sederhana. Jika kita punya matriks A:
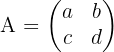
Maka determinannya adalah:
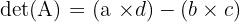
Contoh: Misalkan matriks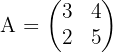 
, maka:
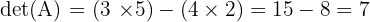
2. Rumus Determinan Matriks 3x3
Untuk mencari determinan matriks 3x3, kamu bisa menggunakan Metode Sarrus atau Metode Minor-Kofaktor.
Cara Menghitung Matriks 3x3 Dengan Metode Sarrus
Misalkan kamu punya matriks 3x3 seperti ini:
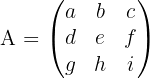
Langkah-langkah untuk menghitung determinannya adalah:
- Salin 2 kolom pertama ke samping matriks: Tambahkan dua kolom pertama dari matriks ke sebelah kanan matriks itu sendiri. Jadi, kamu akan mendapatkan matriks seperti ini:
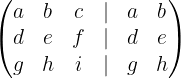
- Hitung perkalian diagonal dari kiri ke kanan (diagonal utama): Kamu perlu mengalikan elemen-elemen diagonal yang berjalan dari kiri atas ke kanan bawah:
- Hitung perkalian diagonal dari kanan ke kiri (diagonal pembalik): Sekarang, kalikan elemen-elemen diagonal yang berjalan dari kanan atas ke kiri bawah:
- Kurangkan hasil diagonal kanan ke kiri dari hasil diagonal kiri ke kanan: Dari langkah 2 dan 3, sekarang kamu punya dua hasil perkalian. Untuk mendapatkan determinannya, tinggal kurangkan hasil diagonal dari kanan ke kiri dengan hasil diagonal dari kiri ke kanan.
Jadi, rumusnya adalah:
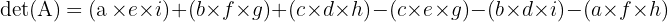
Contoh
Misalnya kita punya matriks:
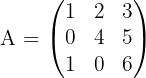
Langkah-langkahnya:
- Salin 2 kolom pertama:
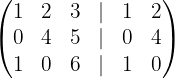
- Hitung perkalian diagonal kiri ke kanan:
Jadi, hasil diagonal kiri ke kanan: 24 + 10 + 0 = 34
- Hitung perkalian diagonal kanan ke kiri:
Jadi, hasil diagonal kanan ke kiri: 12 + 0 + 0 = 12
- Kurangkan hasil diagonal kanan ke kiri dari hasil diagonal kiri ke kanan:
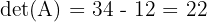
Jadi, determinan matriks A adalah 22.
Periksa di sini untuk les matematika surabaya
Cara Menghitung Matriks 3x3 Dengan Metode Minor-Kofaktor
Metode Minor-Kofaktor adalah cara lain yang bisa digunakan untuk mencari determinan matriks 3x3.
Misalnya kamu memiliki matriks 3x3 seperti ini:
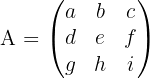
Langkah-langkah menghitung menggunakan metode minor-kofaktor:
- Pilih baris atau kolom untuk dihitung
Biasanya, kita memilih baris atau kolom yang memiliki angka nol, karena itu akan mempermudah perhitungan. Di sini kita akan memilih baris pertama (baris pertama bisa dipilih secara bebas). Misalnya, kita pilih baris pertama: a, b, dan c. - Hitung minor untuk setiap elemen yang dipilih
Minor dari elemen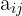
adalah determinan dari matriks kecil yang didapat dengan menghilangkan baris ke-i dan kolom ke-j dari matriks asli. Sebagai contoh: - Minor untuk aa adalah determinan dari matriks yang tersisa setelah menghapus baris pertama dan kolom pertama, yaitu:
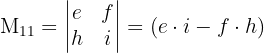
- Minor untuk bb adalah determinan dari matriks yang tersisa setelah menghapus baris pertama dan kolom kedua, yaitu:
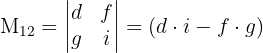
- Minor untuk cc adalah determinan dari matriks yang tersisa setelah menghapus baris pertama dan kolom ketiga, yaitu:
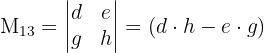
- Hitung kofaktor untuk setiap elemen
Kofaktor adalah minor yang telah dikalikan dengan faktor (−1)i+j(-1)^{i+j}, di mana ii dan jj adalah indeks baris dan kolom elemen tersebut. Jadi, kofaktor dari setiap elemen adalah:- Kofaktor untuk aa adalah
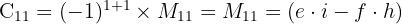
- Kofaktor untuk bb adalah
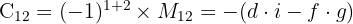
- Kofaktor untuk cc adalah
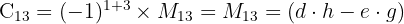
- Kofaktor untuk aa adalah
- Jumlahkan kofaktor yang telah dihitung
Determinan matriks dihitung dengan cara menjumlahkan produk elemen-elemen dari baris pertama dengan kofaktor masing-masing. Rumusnya seperti ini:
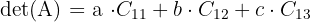
Jadi, substitusi nilai kofaktor yang sudah dihitung:
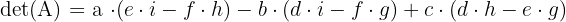
Contoh Perhitungan
Misalkan kita punya matriks berikut:
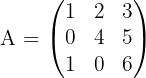
- Hitung minor untuk masing-masing elemen baris pertama:
- Hitung kofaktor:
- Hitung determinan:
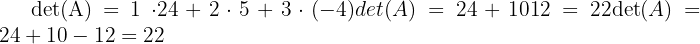
Jadi, determinan matriks A adalah 22.
Temukan les matematika di Medan yang sesuai untuk Anda!
Sifat Determinan Matriks
Determinasi matriks adalah salah satu konsep fundamental dalam aljabar linear yang memiliki peran krusial dalam menentukan keberadaan invers dari sebuah matriks. Sifat-sifat dari determinan matriks tidak hanya membantu kita memahami struktur matriks, tetapi juga memberikan wawasan tentang apakah suatu matriks memiliki invers atau tidak. Berikut adalah beberapa sifat utama dari determinan matriks yang sangat berguna dalam berbagai operasi matematis, terutama dalam konteks invers matriks:
a. Determinan dari Matriks Identitas
Matriks identitas, yang dilambangkan dengan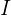 
, adalah matriks persegi yang memiliki elemen 1 pada diagonal utama dan elemen 0 di tempat lain. Determinan dari matriks identitas selalu 1, berapapun ordonya. Secara matematis, ini dinyatakan sebagai:
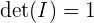
b. Determinan Matriks Singular
Matriks singular adalah matriks yang tidak memiliki invers. Salah satu cara untuk menentukan apakah suatu matriks adalah singular adalah dengan menghitung determinannya. Jika determinan dari sebuah matriks adalah 0, maka matriks tersebut adalah singular dan tidak memiliki invers. Ini adalah salah satu sifat paling penting dari determinan dalam konteks invers matriks:
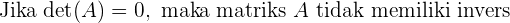
c. Determinan dari Perkalian Matriks
Sifat ini menyatakan bahwa determinan dari hasil perkalian dua matriks sama dengan perkalian dari determinan kedua matriks tersebut. Jika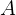 
dan 
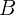adalah dua matriks persegi, maka:
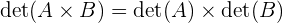
Sifat ini sangat berguna dalam berbagai perhitungan, terutama ketika berurusan dengan matriks yang kompleks.
d. Determinan dari Matriks Transpose
Transpose matriks adalah matriks yang diperoleh dengan menukar elemen-elemen baris menjadi kolom dan sebaliknya. Sifat penting dari determinan menyatakan bahwa determinan dari suatu matriks sama dengan determinan dari transpose-nya:
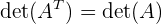
Ini berarti bahwa operasi transpose tidak mengubah nilai determinan suatu matriks.
e. Determinan dari Matriks Invers
Salah satu sifat yang paling relevan dengan pembahasan tentang invers matriks adalah bahwa determinan dari matriks invers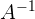 
adalah kebalikan dari determinan matriks :
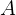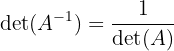
Sifat ini menggarisbawahi pentingnya nilai determinan dalam menentukan eksistensi invers: jika determinan 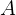nol, maka inversnya tidak ada (karena pembagian dengan nol tidak terdefinisi).
f. Determinan dari Matriks dengan Baris atau Kolom yang Sama
Jika suatu matriks memiliki dua baris atau dua kolom yang identik, maka determinan dari matriks tersebut adalah 0. Ini karena adanya baris atau kolom yang sama menunjukkan ketergantungan linear di antara baris atau kolom, yang mengindikasikan bahwa matriks tersebut singular:
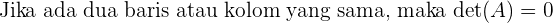
Lihat artikel ini yang membantumu memahami rumus dan deretan geometri!
Invers Matriks
Pengertian Invers Matriks
Secara sederhana, invers matriks adalah kebalikan dari sebuah matriks. Jika kita memiliki matriks A, maka invers dari matriks A, yang dinotasikan sebagai 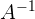, adalah matriks yang jika dikalikan dengan matriks A akan menghasilkan matriks identitas. Matriks identitas sendiri adalah matriks persegi yang memiliki elemen 1 di diagonal utama dan 0 di elemen lainnya. Dalam bentuk matematis, hubungan ini dapat dituliskan sebagai:
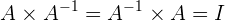
Di mana I adalah matriks identitas. Matriks yang memiliki invers disebut sebagai matriks non-singular atau matriks invertible. Sebaliknya, jika sebuah matriks tidak memiliki invers, maka matriks tersebut disebut sebagai matriks singular.
Inilah tempat kursus matematika terbaik yang bisa membantu Anda memahami matematika lebih dalam!
Invers Matriks 2x2
Salah satu cara yang paling sederhana untuk menghitung invers matriks adalah pada matriks berordo 2x2. Misalkan kita memiliki matriks A berordo 2x2 sebagai berikut:
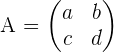
Rumus invers matriks 2x2 dapat dituliskan sebagai:
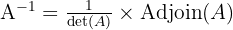
yang mana adjoin matriks 2x2 dapat ditulis: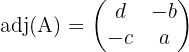
Di sini,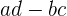 
disebut sebagai determinan dari matriks A. Agar matriks A memiliki invers, nilai determinan 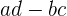harus tidak sama dengan nol. Jika determinan sama dengan nol, maka matriks tersebut tidak memiliki invers, atau dengan kata lain, matriks tersebut adalah matriks singular.
Cara Menghitung Invers Berordo 3x3 Dengan Metode Adjoin Matriks 3x3
Adjoin matriks adalah matriks yang diperoleh dengan mengambil kofaktor dari setiap elemen dalam matriks tersebut, kemudian melakukan transposisi. Proses ini cukup panjang, terutama untuk matriks dengan ordo yang lebih besar, seperti 3x3. Berikut adalah langkah-langkah untuk menghitung invers matriks 3x3 menggunakan metode adjoin:
- Menentukan Kofaktor: Untuk setiap elemen dalam matriks, kita perlu menghitung kofaktornya. Kofaktor adalah determinan dari sub-matriks yang diperoleh dengan menghilangkan baris dan kolom yang berisi elemen tersebut.
- Membuat Matriks Kofaktor: Setelah semua kofaktor dihitung, kita dapat menyusun matriks kofaktor, yang elemen-elemennya adalah kofaktor dari elemen-elemen matriks asal.
- Transposisi Matriks Kofaktor: Transposisi matriks kofaktor dilakukan dengan menukar elemen-elemen pada baris dan kolom.
- Menghitung Adjoin Matriks: Matriks adjoin adalah transposisi dari matriks kofaktor yang telah kita hitung.
- Menghitung Determinan Matriks Asal: Langkah ini penting karena invers matriks adalah hasil kali dari adjoin matriks dengan kebalikan dari determinan matriks asal.
- Menghitung Invers Matriks: Invers dari matriks asal adalah adjoin matriks yang telah dihitung, dibagi dengan determinan matriks asal.
Secara matematis, invers dari matriks A yang berordo 3x3 dapat dituliskan sebagai:
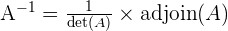
Di mana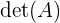 
adalah determinan dari matriks A, dan 
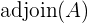adalah adjoin dari matriks A.
Pembagian Matriks
Dalam aljabar linear, pembagian matriks tidak dapat dilakukan secara langsung seperti pada bilangan biasa. Namun, pembagian matriks dapat dilakukan dengan cara mengalikan matriks dengan invers dari matriks lainnya. Misalnya, jika kita ingin membagi matriks A dengan matriks B, secara matematis ini dapat dituliskan sebagai:
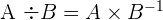
Di sini,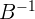 
adalah invers dari matriks B. Oleh karena itu, untuk melakukan pembagian matriks, kita harus terlebih dahulu menghitung invers dari matriks yang menjadi pembagi.
Contoh Soal dan Pembahasan
Agar lebih paham dengan rumus-rumus di atas, simak contoh selengkapnya berikut ini.
- Terdapat dua matriks, yaitu matriks A dan B seperti berikut:
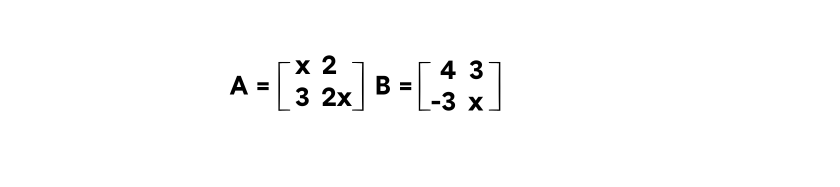
Agar determinan matriks A sama dengan dua kali determinan B, maka nilai x yang memenuhi adalah...
Jawab:
Kita cari determinan matriks A dan B masing-masing menggunakan operasi silang,
|A| = ab – bc = 2x² - 6
|B| = ab – bc = 4x – (-9) = 4x + 9
Karena determinan matriks A sama dengan 2 kali determinan matriks B, maka
|A| = 2|B|
2x² - 6 = 2(4x + 9)
2x² – 6 = 8x + 18
2x² – 8x = 18 + 6
2x² – 8x = 24
2x² – 8x – 24 = 0
x² – 4x – 12 = 0
Kita cari akar-akarnya:
( x -6 ) (x + 2 ) =0
x – 6 = 0
x = 6
x + 2 = 0
x = -2
Jadi, akar-akarnya adalah x = 6 dan x = -2
- Tentukan determinan dari matriks di bawah ini.
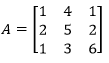
Jawab:
Menggunakan aturan Sarrus, maka
|A| = aei + bfg + cdh – ceg – afh – bdi
|A| = (1x5x6) + (4x2x1) + (1x2x3) – (1x5x1) – (1x2x3) – (4x2x6)
|A| = 30 + 8 + 6 – 5 – 6 – 48
|A| = -15
Jadi, determinan matriks A adalah -15.
- Tentukan determinan dari matriks A berikut.
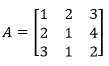
Jawab:
Menggunakan metode minor-kofaktor, determinan A adalah:
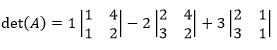
det(A) = = 1(-2) – 2(-8) + 3(-1) = -2 + 16 -3 = 11
Jadi, determinan dari matriks A adalah 11.
- Tentukanlah invers dari matriks berikut.
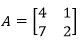
Jawab:
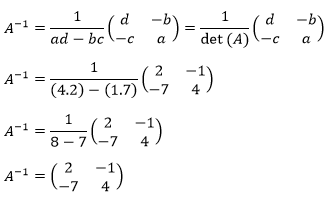
Jadi, invers matriks A adalah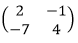 
5. Diberikan matriks A sebagai berikut:
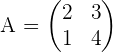
Hitunglah invers dari matriks A.
Pembahasan:
Langkah pertama adalah menghitung determinan dari matriks A:
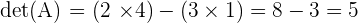
Karena determinan tidak sama dengan nol, kita bisa melanjutkan dengan menghitung invers matriks:
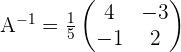
Sehingga invers dari matriks A adalah:
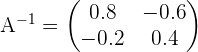
Kesulitan Belajar Matematika? Ini Solusinya!
Matematika memang tidak selalu mudah, terutama ketika kamu berurusan dengan konsep-konsep seperti rumus determinan, transpose matriks, dan adjoin matriks. Tapi jangan khawatir! Jika kamu merasa kesulitan memahami materi matriks atau cara menghitung matriks, kamu tidak sendirian.
Di Superprof, ada banyak guru privat yang siap membantu kamu memahami materi ini lebih dalam dengan cara yang mudah dan menyenangkan. Kamu bisa memilih guru yang sesuai dengan gaya belajarmu dan belajar dengan kecepatan yang kamu tentukan sendiri. Jadi, kalau kamu merasa butuh bantuan untuk menguasai materi matriks, rumus invers, atau operasi matriks lainnya, kunjungi Superprof dan cari les privat yang cocok untukmu!
Jika Anda belum terlalu paham tentang materi matematika lainnya seperti rumus trigonometri, Kami akan membantu Anda. Selamat belajar!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
