Sebelum masuk lebih jauh ke pembahasan rumus luas segitiga, kita pahami dulu tujuan utama belajar matematika yuk! Pada dasarnya, matematika itu punya tujuan untuk membantu kamu terutama para siswa-siswi membangun pemahaman konsep yang benar, bukan sekadar menghafal rumus. Dengan begitu, para siswa-siswi harapannya mampu menerapkan konsep tersebut dalam kehidupan sehari-hari.
Materi matematika tentang luas segitiga, khususnya segitiga siku-siku, biasanya dianggap sederhana. Padahal, dalam praktik nyata, banyak para siswa dan siswi justru merasa kesulitan saat menghitung luas segitiga. Hal ini biasanya terjadi karena proses belajar yang dilakukan secara langsung tanpa dukungan media pembelajaran dan penanaman konsep dasar yang tepat. Akibatnya, ketika peserta didik belum benar-benar memahami konsep awal cara menghitung luas segitiga, materi yang sudah dipelajari jadi lebih cepat terlupakan.
Cara Menentukan Luas Segitiga
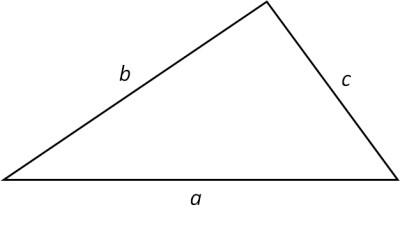
Sekarang kita masuk ke pembahasan cara mencari luas segitiga. Sebenarnya, menentukan luas segitiga itu bukan hal yang rumit, asalkan kamu sudah memahami rumus dasarnya.
Seperti yang sudah dijelaskan sebelumnya, rumus segitiga untuk mencari luas adalah:
L = ½ × alas × tinggi
Jadi, cara menghitung luas segitiga cukup dengan mengalikan setengah dari nilai alas dengan tinggi segitiga tersebut. Dalam banyak soal matematika, biasanya nilai alas dan tinggi sudah diketahui, sehingga kamu bisa langsung melakukan perhitungan tanpa kesulitan berarti.
Rumus Luas Segitiga
Setelah kamu memahami rumus luas segitiga, langkah berikutnya adalah menerapkannya dalam perhitungan.
Contohnya :
Diketahui sebuah segitiga punya panjang alas 6 cm dan tinggi 7 cm. Untuk menghitung luas segitiga, kamu gunakan rumus:
L = ½ × alas × tinggi
L = ½ × 6 × 7
L = ½ × 42
L = 21 cm²
Dari proses perhitungan diatas, beda dengan bangun ruang, bisa disimpulkan jika luas segitiga adalah 21 cm². Hal ini menunjukkan rumus mencari luas segitiga sangat mudah diterapkan apabila nilai alas dan tinggi sudah diketahui.
Jenis-Jenis Segitiga dan Rumusnya
1. Segitiga Berdasarkan Panjang Sisi
a. Segitiga Sama Sisi
Segitiga sama sisi adalah segitiga yang memiliki ketiga sisi sama panjang. Contohnya segitiga dengan panjang sisi 6 cm, 6 cm, dan 6 cm. Karena semua sisinya sama, segitiga ini memiliki tinggi tertentu yang bisa ditentukan, sehingga luas segitiga dapat dihitung menggunakan rumus segitiga umum: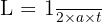
b. Segitiga Sama Kaki
Beda dengan kerucut, segitiga sama kaki memiliki dua sisi yang sama panjang, misalnya 5 cm, 5 cm, dan alas 8 cm. Untuk menghitung luas segitiga jenis ini, kamu perlu menentukan tinggi segitiganya terlebih dahulu, lalu menggunakan rumus: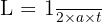
c. Segitiga Sembarang
Segitiga sembarang adalah segitiga dengan panjang sisi yang berbeda-beda, misalnya 4 cm, 6 cm, dan 9 cm. Jika tinggi segitiga diketahui, maka rumus luas segitiga sembarang tetap menggunakan rumus dasar :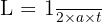
Namun, jika yang diketahui hanya ketiga sisinya, maka rumus luas segitiga sembarang dapat dihitung menggunakan rumus Heron :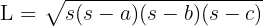
dengan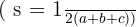 
.
2. Segitiga Berdasarkan Besar Sudut
a. Segitiga Lancip
Segitiga lancip memiliki semua sudut kurang dari 90°, misalnya 50°, 60°, dan 70°. Jika diketahui dua sisi dan sudut apitnya, maka luas segitiga dapat ditentukan menggunakan pendekatan rumus trigonometri :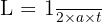
b. Segitiga Siku-Siku
Segitiga siku-siku memiliki satu sudut 90°, misalnya sudut 90°, 30°, dan 60°. Karena alas dan tinggi saling tegak lurus, cara menghitung luas segitiga pada segitiga ini bisa langsung menggunakan rumus dasar :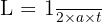
Alas dan tinggi merupakan sisi-sisi yang saling tegak lurus.
c. Segitiga Tumpul
Segitiga tumpul memiliki satu sudut lebih dari 90°, misalnya 110°, 40°, dan 30°. Jika diketahui dua sisi dan sudut di antaranya, maka luas segitiga dapat dihitung menggunakan rumus trigonometri :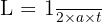
Contoh Soal 1 (Rumus Dasar: Alas dan Tinggi)
Soal:
Sebuah segitiga memiliki panjang alas 10 cm dan tinggi 8 cm. Tentukan luas segitiga tersebut.
Penyelesaian:
Rumus luas segitiga: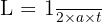
Substitusikan nilai yang diketahui: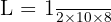
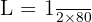
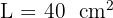
Jawaban:
Jadi, luas segitiga tersebut adalah 40 cm².
Contoh Soal 2 (Rumus Trigonometri: Dua Sisi dan Sudut Apit)
Soal:
Diketahui sebuah segitiga memiliki panjang sisi a = 7 cm dan b = 9 cm dengan sudut apit 30°. Hitung luas segitiga tersebut.
Penyelesaian: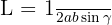
Substitusi nilai: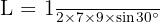
Karena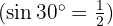 
, maka: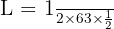
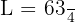
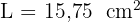
Jawaban:
Luas segitiga tersebut adalah 15,75 cm².
Rumus dan Cara Menentukan Keliling Segitiga
Konsep keliling segitiga ini penting karena sering digunakan sebagai dasar berbagai perhitungan geometri.
Kamu perlu tau, keliling bangun datar merupakan jumlah dari seluruh panjang sisi yang membentuk bangun datar, termasuk segitiga. Karena segitiga punya tiga sisi, maka keliling segitiga bisa dihitung menggunakan rumus:
K = a + b + c
Contoh Soal Keliling Segitiga
Keliling segitiga merupakan jumlah seluruh panjang sisi yang membentuk segitiga. Dalam pembelajaran matematika kelas VII, konsep rumus keliling segitiga ini digunakan untuk melatih pemahaman peserta didik terhadap bangun datar segitiga.
Berikut rumus keliling segitiga :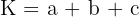
dengan a, b, dan c menyatakan panjang ketiga sisi segitiga.
Contoh Soal:
Diketahui segitiga ABC punya panjang sisi AB = 4 cm, BC = 5 cm, dan CA = 3 cm. Tentukan kelilingnya!
Penyelesaian:
Diketahui:
AB = 4 cm
BC = 5 cm
CA = 3 cm
Keliling segitiga dihitung dengan menjumlahkan seluruh panjang sisi: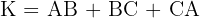
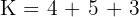
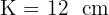
Jadi, keliling segitiga ABC adalah 12 cm.
Kesimpulan
Dari pembahasan materi di atas, untuk memahami rumus segitiga tidak hanya soal menghafal, tetapi juga memahami konsep. Dengan rumus keliling dan luas segitiga, sampai rumus luas segitiga sembarang, kamu jadi lebih mudah menghitung luas segitiga serta memahami hubungan antara luas dan keliling segitiga secara menyeluruh. Jika konsep dasarnya sudah dipahami, berbagai soal tentang keliling dan luas segitiga tentu bisa diselesaikan dengan lebih percaya diri.
Kalau kamu merasa belajar rumus segitiga sendirian itu membingungkan, nggak ada salahnya coba kelas privat matematika biar ada pembimbing. Di Superprof, kamu bisa ketemu tutor matematika yang siap jelasin rumus luas dan keliling segitiga, sampai cara menghitung luas segitiga dengan cara yang mudah dipahami. Kamu juga bisa belajar mean median modus dalam matematika. Belajar jadi lebih praktis dan bikin proses belajar jadi lebih menyenangkan.
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
