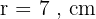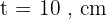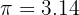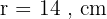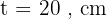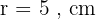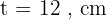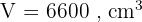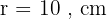Selain bangun ruang kubus dan balok, tabung termasuk salah satu bangun ruang yang mudah kita temui di sekitar kita. Misalnya di dapur, ada banyak benda-benda yang berbentuk tabung, seperti pipa, botol air minum, ember, kaleng kemasan makanan, dan masih banyak lainnya. Pernahkah terlintas untuk menghitung volume dan luas permukaan benda-benda tersebut? Ya, Anda bisa menggunakan rumus tabung.
Kali ini, kita akan sedikit banyak membahas tentang tabung. Terutama mengenai rumus tabung, cara mencari luas tabung serta cara menghitung volume tabung. Latihan soal akan membantu Anda untuk memahaminya lebih jauh. Tapi sebelum membahas itu, kami juga akan memberi pengantar sekilas mengenai apa itu tabung beserta mengenal sifat-sifatnya. Pemahaman konsep terkait tabung dan karakteristiknya membantu siswa untuk memahami penggunaan rumus luas tabung.
Siswa matematika yang ingin berhasil dengan semua rumus dan konsep matematika yang kompleks perlu memperbanyak latihan soal. Matematika tidak bisa hanya dengan menghafal, siswa juga dituntut untuk banyak mengerjakan contoh-contoh soal agar terbiasa menyelesaikan setiap permasalahan dalam matematika. Dalam banyak kasus, soal-soal matematika tidak dapat dikerjakan secara langsung menggunakan rumus matematika, diperlukan adanya pemahaman logika dan nalar yang baik untuk memahami maksud soal. Perlu diketahui bahwa ada banyak manfaat belajar matematika!
Mengenal apa itu tabung dan sifat-sifatnya
Tabung dan cara menghitung luas permukaan tabung merupakan materi matematika di tingkat sekolah menengah. Siswa akan diperkenalkan dengan macam-macam bangun ruang yang diantaranya adalah tabung.
Rumus luas tabung merupakan bangun ruang yang memiliki alas dua sisi yang konguren dan juga sejajar berbentuk lingkaran dan sisi lengkung.
Sementara, tabung adalah sebuah bangun dari ruang tiga dimensi yang memiliki tutup serta atas berbentuk sebuah lingkaran dan memiliki ukuran yang sama dan diselimuti persegi panjang.
Jika dibuka, jaring-jaring tabung berbentuk dua buah lingkaran yakni alas dan tutupnya serta persegi panjang yang menyelimuti tabung tersebut.
Temukan guru privat untuk les olimpiade matematika Jakarta.
Untuk lebih mengenal karakteristik tabung, adapun sifat-sifat tabung sebagai berikut;
- Bagian tabung terdiri dari sisi tegak yang berupa bidang lengkung atau disebut selimut tabung dan bidang alas serta tutup yang berupa lingkaran
- Tabung memiliki dua rusuk, yakni rusuk alas dan tutup
- Tabung memiliki 3 sisi yang terdiri dari alas, selimut atau selubung, dan tutup
- Tinggi tabung merupakan jarak antara alas dengan tutup tabung
- Sisi alas serta tutup tabung berbentuk lingkaran dan sama besar (jari-jarinya sama besar)
Ada banyak benda-benda di sekitar berbentuk tabung yang membantu kita memahami wujud tabung sebenarnya, misalnya kaleng kemasan makanan, pipa, tiang bendera, botol air minum, dll.
Maka sudahkah Anda memahami bentuk tabung beserta sifat-sifatnya? Coba sebutkan benda-benda lainnya di sekitar Anda yang berbentuk tabung!
Baca juga: Apa itu limas?
Bagian-Bagian Bentuk Tabung
Tabung memiliki Bentuk yang sangat khas dan mudah. Bangun ruang ini memiliki bagian-bagian penting yang berguna untuk menghitung volume, luas permukaan, dan kelilingnya dengan tepat. Inilah bagian utama dari tabung, yaitu:
- Alas dan Tutup Tabung
Kedua bagian ini berbentuk lingkaran yang identik dan sejajar. Kedua lingkaran ini memiliki jari-jari yang sama, yang digunakan dalam perhitungan volume dan luas permukaan tabung. - Selimut Tabung
Selimut tabung adalah bagian melengkung yang menghubungkan alas dan tutup tabung. Selimut ini, jika dibuka, akan berbentuk persegi panjang dengan panjang yang sama dengan keliling alas dan lebar yang sama dengan tinggi tabung. - Jari-Jari (r)
Jari-jari merupakan jarak dari pusat lingkaran (baik pada alas maupun tutup) menuju tepi lingkaran. Jari-jari ini digunakan untuk menghitung luas alas dan volume tabung. - Tinggi (t)
Merupakan jarak tegak lurus antara alas dan tutup tabung. Tinggi tabung penting untuk perhitungan volume dan luas permukaan tabung.
Reservasi sekarang guru matematika SMP yang ada di lokasi tempat tinggal Anda.
Rumus Volume dan Luas Permukaan Tabung
Tabung merupakan bangun ruang yang sangat berguna dalam berbagai kehidupan sehari-hari, baik untuk menghitung volume air dalam drum atau menentukan luas bahan yang dibutuhkan untuk membuat kaleng minuman. Agar lebih mudah menghitung volume dan luas permukaan tabung, kita perlu mengenal rumus dasar yang digunakan.
Rumus Volume Tabung
Cara menghitung volume tabung sangatlah sederhana. Rumus tabung volume dihitung dengan mengalikan luas alas tabung dengan tinggi tabung. Alas tabung berbentuk lingkaran, sehingga kita gunakan rumus luas lingkaran untuk menghitungnya. Secara matematis, rumus volume tabung adalah:
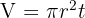
Di mana:
- V = volume tabung
- r = jari-jari alas tabung
- t= tinggi tabung
= konstanta Pi (3.14 atau 22/7)
Rumus Luas Permukaan Tabung dengan Tutup
Untuk menghitung lp tabung, kita perlu menghitung luas dua lingkaran (alas dan tutup) serta luas selimut tabung yang mengelilinginya. Rumus untuk menghitung luas permukaan tabung dengan tutup adalah:
Di mana:
- L = luas permukaan tabung
- r = jari-jari alas tabung
- t = tinggi tabung
Luas permukaan tabung ini mencakup dua lingkaran yang menjadi alas dan tutup tabung, ditambah dengan luas sisi selimut tabung yang melengkung menghubungkan kedua alas tersebut.
Luas Permukaan Tabung Tanpa Tutup
Untuk bangun ruang tabung tanpa tutup, kita hanya menghitung luas alas dan luas selimutnya. Rumus luas permukaan tabung tanpa tutup adalah:
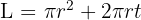
Di mana:
- L = luas permukaan tabung
- r = jari-jari alas tabung
- t = tinggi tabung
Rumus ini digunakan ketika tabung tidak memiliki tutup di bagian atas, misalnya pada beberapa jenis pipa atau ember yang terbuka.
Luas Selimut Tabung
Luas selimut tabung adalah luas permukaan bagian melengkung yang menghubungkan alas dan tutup tabung. Rumus untuk menghitung luas selimut tabung adalah:
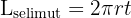
Di mana:
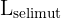= luas selimut tabung- r = jari-jari alas tabung
- t = tinggi tabung
Luas selimut tabung ini penting untuk menghitung bahan yang dibutuhkan untuk menutupi sisi tabung tanpa memperhitungkan alas atau tutupnya.
Baca juga: Cara menghitung luas dan keliling persegi panjang
Contoh Soal Volume dan Luas Permukaan Tabung
Untuk lebih memahami rumus-rumus di atas, mari kita lihat beberapa contoh soal yang akan membantu Anda memahami cara menghitung volume dan luas permukaan tabung.
Contoh 1
Diketahui sebuah tabung dengan jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut!
Penyelesaian:
Diketahui:
Gunakan rumus volume tabung: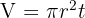
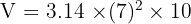
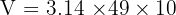
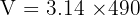
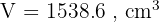
Jadi, volume tabung tersebut adalah 1538.6 cm³.
Contoh 2
Diketahui sebuah tabung dengan jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah luas permukaan tabung tersebut!
Penyelesaian:
Diketahui:
Gunakan rumus luas permukaan tabung:
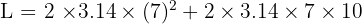
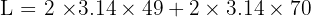
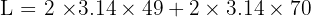
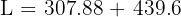
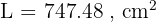
Jadi, luas permukaan tabung tersebut adalah 747.48 cm².
Contoh 3
Diketahui sebuah tabung tanpa tutup memiliki jari-jari alas 14 cm dan tinggi 20 cm. Hitunglah luas permukaannya!
Penyelesaian:
Diketahui:
Gunakan rumus luas permukaan tabung tanpa tutup:
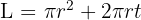
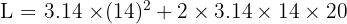
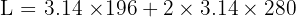
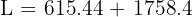
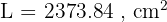
Jadi, luas permukaan tabung tanpa tutup tersebut adalah 2373.84 cm².
Contoh 4
Diketahui sebuah tabung dengan jari-jari alas 5 cm dan tinggi 12 cm. Hitunglah luas selimut tabung!
Penyelesaian:
Diketahui:
Gunakan rumus luas selimut tabung:
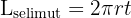
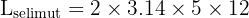
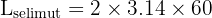
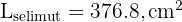
Jadi, luas selimut tabung tersebut adalah 376.8 cm².
Contoh 5
Diketahui volume sebuah tabung 6.600 cm³, dengan jari-jari 10 cm. Berapa tinggi tabung?
Penyelesaian:
Diketahui:
Gunakan volume tabung rumus:
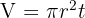
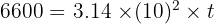
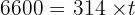
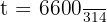
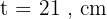
Jadi, tinggi tabung tersebut adalah 21 cm.
Baca juga: Rumus balok dan kubus
Tabung adalah salah satu bangun ruang yang sangat berguna dalam kehidupan sehari-hari. Dengan menguasai rumus volume dan luas permukaan tabung, Anda dapat menghitung kapasitas dan kebutuhan bahan dengan praktis.
Jika Anda merasa kesulitan dengan konsep matematika diatas, bergabunglah dengan les matematika di Superprof. Dengan tutor berpengalaman, Anda dapat memperdalam pemahaman dan memperoleh bantuan untuk menguasai rumus-rumus matematika dengan cara yang mudah dan menyenangkan. Tak perlu ragu, daftar sekarang dan raih pemahaman matematika yang lebih baik!
Baca juga: Menghitung luas dan volume bola
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
