Teori peluang, atau dalam matematika sering disebut dengan probabilitas, adalah konsep yang tidak hanya berguna di dalam ujian matematika kelas 12, tetapi juga bisa kamu aplikasikan dalam kehidupan sehari-hari. Bayangkan, setiap kali kamu menunggu hasil ujian, melirik prakiraan cuaca, atau bahkan ketika kamu memilih baju yang tepat, tanpa sadar kamu sedang menghitung peluang! Oleh karena itu, memahami materi peluang kelas 8 sangat penting. Tidak hanya untuk ujian, tetapi juga untuk memahami kejadian-kejadian yang terjadi di sekitar kita.
Untuk membantu Anda memahami lebih lanjut terkait Materi Peluang Kelas 12, yuk simak penjelasan berikut ini!
Cek disini untuk les privat matematika terbaik
Apa itu Rumus Sampel?
Rumus sampel merujuk pada himpunan semua hasil yang mungkin dari suatu percobaan acak. Dalam konteks teori peluang, sampel ini seringkali dinotasikan dengan huruf S. Misalnya, jika kita melempar sebuah koin, maka ruang sampel (S) dari percobaan ini adalah {H, T}, di mana H mewakili "Head" (angka) dan T mewakili "Tail" (gambar). Ruang sampel membantu kita untuk memahami semua kemungkinan yang mungkin terjadi dalam percobaan tersebut.
Untuk menghitung peluang terjadinya suatu kejadian dalam ruang sampel, kita menggunakan rumus probabilitas. Rumus probabilitas dasar untuk menghitung peluang suatu kejadian adalah:
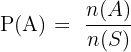
Di sini, P(A) adalah peluang kejadian A, n(A) adalah jumlah hasil yang mendukung kejadian A, dan n(S) adalah total jumlah hasil dalam ruang sampel S.
Contoh Menghitung Peluang dengan Ruang Sampel
Misalkan kita memiliki kotak yang berisi 5 bola merah dan 3 bola biru. Jika kita mengambil satu bola secara acak, berapa peluang terambilnya bola merah?
Ruang sampel untuk kejadian ini adalah semua bola yang ada di dalam kotak, yaitu:
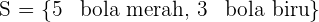
Jadi, n(S) = 8.
Untuk kejadian terambilnya bola merah, kita memiliki 5 bola merah, jadi n(A) = 5.
Peluang terambilnya bola merah adalah:
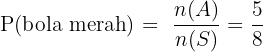
Definisi Peluang dan Peluang Teoritik
Seringkali saat Anda hendak bepergian, Anda memeriksa prakiraan cuaca hari itu untuk memastikan apakah akan terjadi hujan atau tidak. Seringnya, Anda memeriksanya berulang kali. Tanpa disadari, kondisi demikian menandakan bahwa Anda sedang menerapkan prinsip peluang.
Lantas apa yang dimaksud peluang matematika?
Teori peluang adalah kemungkinan terjadinya suatu kejadian dalam suatu percobaan. Dengan kata lain, peluang menggambarkan seberapa besar kemungkinan sebuah peristiwa terjadi. Peluang ini selalu memiliki nilai antara 0 dan 1. Nilai 0 menunjukkan bahwa kejadian tersebut tidak mungkin terjadi, sedangkan nilai 1 menunjukkan bahwa kejadian tersebut pasti terjadi.
Dalam kehidupan sehari-hari, kita sering menggunakan peluang untuk membuat prediksi. Misalnya, peluang cuaca hujan, peluang menang dalam permainan, atau bahkan peluang diterima di kampus impian!
Peluang teoritik adalah peluang yang dihitung berdasarkan asumsi bahwa semua hasil yang mungkin dari suatu percobaan memiliki kesempatan yang sama untuk terjadi. Peluang ini dihitung menggunakan rumus probabilitas dasar yang telah disebutkan di atas.
Ada beberapa istilah dalam peluang yang wajib Anda pahami agar dapat mempelajari materi peluang lebih lanjut. Diantaranya;
- Percobaan peluang adalah kegiatan yang tujuannya untuk memperoleh hasil tertentu. Contohnya adalah pelemparan uang koin, pelemparan dadu, pengambil kartu bridge, dll.
- Ruang sampel. Disimbolkan dengan S, ruang sampel adalah himpunan semua hasil yang mungkin terjadi dari suatu percobaan. Misalnya menentukan rumus ruang sampel dari percobaan pelemparan satu buah koin, maka S={angka, gambar}.
- Titik Sampel. Setiap anggota ruang sampel disebut dengan titik sampel. Jika menggunakan contoh yang sama seperti sebelumnya, maka titik sampel pada kejadian pelemparan satu buah koin adalah sisi gambar dan angka. Jumlah titik sampel dinotasikan dengan n(S). Dalam menentukan titik sampel ini, ada tiga cara yang dapat Anda lakukan, dengan menggunakan teknik diagrampohon, diagram tabel, maupun dengan mencacah langsung anggotanya.
- Frekuensi. Frekuensi dalam peluang adalah banyaknya hasil tertentu yang sama dan teramati.
- Frekuensi relatif. Sementara, frekuensi relatif adalah hasil peluang tertentu yang muncul dari sejumlah percobaan.
Kenali juga apa itu matriks dalam matematika!
Rumus Peluang Suatu Kejadian
Peluang dapat dihitung menggunakan rumus yang melibatkan perbandingan antara jumlah kejadian yang diinginkan dengan total kejadian. Oleh karena itu, Rumus peluang kejadian dapat ditulis sebagai:
P(A) =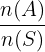 
Dimana:
- P(A) adalah peluang terjadinya kejadian A,
- n(A) adalah banyaknya elemen dalam kejadian A yang diinginkan,
- n(S) adalah banyaknya elemen dalam ruang sampel, atau total kemungkinan yang ada.
Adapun sifat-sifat peluang yang perlu Anda pehatikan adalah;
- Kisaran nilai peluang suatu kejadian adalah antara 0 sampai dengan 1 atau 0 ≤ P(A) ≥ 1
- P(A) = 0 artinya peluang suatu kejadian yang tidak mungkin terjadi.
- P(A) = 1 artinya peluang suatu kejadian yang pasti terjadi
Dari sifat peluang tersebut dapat ditarik kesimpulan bahwa nilai peluang tidak mungkin bernilai kurang dari 1 dan lebih dari 1.
Sebagai contoh, jika kita memiliki dadu enam sisi dan kita ingin menghitung peluang munculnya angka 3, maka peluang teoritiknya adalah:
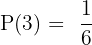
Karena ada satu angka 3 di antara enam kemungkinan hasil (1, 2, 3, 4, 5, 6).
Periksa di sini untuk les matematika online
Jenis-jenis peluang
Peluang dibagi menjadi dua kategori utama, yaitu peluang tunggal dan peluang majemuk. Berikut adalah jenis-jenis peluang yang perlu kamu ketahui:
1. Peluang Tunggal (Single Event Probability)
Peluang tunggal mengacu pada kemungkinan terjadinya satu kejadian spesifik dalam suatu percobaan atau situasi. Peluang ini adalah jenis yang paling sederhana dan sering diajarkan pertama kali dalam teori peluang. Dalam konteks matematis, peluang tunggal dihitung dengan membagi jumlah kejadian yang memenuhi syarat dengan jumlah total kemungkinan hasil dalam ruang sampel.
Misalnya, ketika kita melempar sebuah dadu enam sisi, peluang munculnya angka 6 adalah contoh dari peluang tunggal. Karena hanya ada satu angka 6 dari enam kemungkinan hasil (1, 2, 3, 4, 5, 6), peluangnya dihitung sebagai:
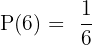
Contoh lain adalah ketika kita menarik satu kartu dari setumpuk kartu remi standar, peluang mendapatkan kartu As Hati adalah peluang tunggal. Dengan satu kartu As Hati dari 52 kartu, peluangnya adalah:
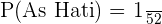
2. Peluang Majemuk
Peluang majemuk melibatkan dua kejadian atau lebih dalam satu percobaan. Peluang majemuk dapat dibagi menjadi beberapa jenis tergantung pada hubungan antara kejadian-kejadian tersebut.
a. Peluang Kejadian Saling Lepas
Kejadian saling lepas adalah dua kejadian yang tidak bisa terjadi secara bersamaan. Artinya, jika salah satu kejadian terjadi, kejadian lainnya tidak mungkin terjadi pada saat yang sama.
Rumus Peluang Kejadian Saling Lepas:
= P(A) + P(B)
Contoh Soal Kejadian Saling Lepas:
Misalnya kita melempar sebuah dadu, dan kita ingin menghitung peluang munculnya angka 2 atau angka 4. Karena kedua kejadian ini tidak mungkin terjadi bersamaan, kita bisa menjumlahkan peluang kedua kejadian:
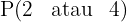= P(2) + P(4)
= 
+
= 
= 
Jika menurut kalian materi ini terlalu mudah, cobalah baca materi tentang aturan dan rumus trigonometri!
b. Peluang Kejadian Tidak Saling Lepas
Kejadian tidak saling lepas adalah dua kejadian yang bisa terjadi bersamaan. Artinya, kedua kejadian ini dapat terjadi dalam satu percobaan.
Rumus Peluang Kejadian Tidak Saling Lepas:
= P(A) + P(B) -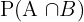 
Dimana 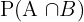adalah peluang kedua kejadian terjadi bersamaan.
Contoh Soal Kejadian Tidak Saling Lepas:
Misalnya, kita memiliki kotak dengan 10 bola merah dan 5 bola biru. Kita menarik satu bola, dan kita ingin tahu peluang mendapatkan bola merah atau bola biru. Peluang masing-masing kejadian:
= 
,
= 
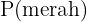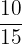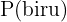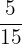
Namun, dalam hal ini, kejadian tidak saling lepas karena kedua jenis bola bisa ada dalam satu percobaan. Maka kita hitung peluangnya:
= + 
- 
= + 
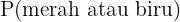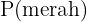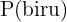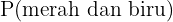
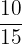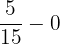
= 1
c. Peluang Kejadian Saling Bebas
Kejadian saling bebas adalah dua kejadian yang tidak mempengaruhi satu sama lain. Artinya, hasil dari satu kejadian tidak mempengaruhi hasil kejadian lainnya.
Rumus Peluang Kejadian Saling Bebas:
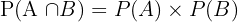
Contoh Soal Kejadian Saling Bebas:
Misalnya, kita melempar dua dadu sekaligus, dan kita ingin tahu peluang munculnya angka genap pada dadu pertama dan angka ganjil pada dadu kedua. Karena hasil pelemparan dadu pertama tidak mempengaruhi hasil pelemparan dadu kedua, ini adalah kejadian saling bebas.
Peluang muncul angka genap di dadu pertama adalah (A) = 
(karena ada 3 angka genap: 2, 4, dan 6).
Peluang muncul angka ganjil di dadu kedua adalah P(B) = (karena ada 3 angka ganjil: 1, 3, dan 5).
Maka peluang kedua kejadian saling bebas terjadi adalah:
= 
= 
= 
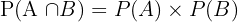
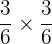
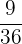
Temukan sekarang les matematika surabaya!
d. Peluang Kejadian Tidak Saling Bebas
Kejadian tidak saling bebas atau kejadian bersyarat adalah kejadian yang mempengaruhi satu sama lain. Artinya, hasil dari satu kejadian bisa mempengaruhi kejadian lainnya.
Rumus Peluang Kejadian Tidak Saling Bebas:
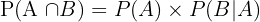
Dimana P(B|A) adalah peluang terjadinya B setelah A terjadi.
Contoh Soal Peluang Kejadian Tidak Saling Bebas:
Misalnya, kamu menarik dua bola dari kotak yang berisi 10 bola merah dan 5 bola biru tanpa pengembalian. Peluang terambilnya bola merah pada pengambilan pertama adalah P(A) = .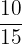
Peluang terambilnya bola merah pada pengambilan kedua, setelah bola pertama diambil (tanpa pengembalian), adalah P(B|A) =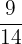 
.
Maka peluang kedua kejadian tidak saling bebas terjadi adalah:
= 
= 
= 
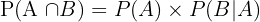
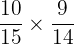
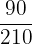
Contoh Soal Peluang
Sekarang, mari kita lihat beberapa contoh soal peluang kelas 12 untuk memperjelas bagaimana semua konsep ini bekerja.
Contoh Soal 1: Peluang Munculnya Mata Dadu Bilangan Genap
Diberikan sebuah dadu yang memiliki enam sisi. Tentukan peluang munculnya mata dadu yang genap.
Pembahasan:
- Ruang sampel (n(S)) = {1, 2, 3, 4, 5, 6} → n(S) = 6
- Kejadian yang diinginkan adalah angka genap (A) = {2, 4, 6} → n(A) = 3
Peluang munculnya mata dadu genap:
P(A) =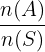
=
= 
Contoh Soal 2: Peluang Munculnya Mata Dadu Bilangan Prima
Tentukan peluang munculnya mata dadu yang merupakan bilangan prima.
Pembahasan:
- Ruang sampel (n(S)) = {1, 2, 3, 4, 5, 6} → n(S) = 6
- Kejadian yang diinginkan adalah angka prima (A) = {2, 3, 5} → n(A) = 3
Peluang munculnya mata dadu bilangan prima:
P(A) =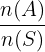
=
=
Cek di sini untuk kursus matematika
Selain itu, ada juga soal peluang yang memperhatikan urutan/susunannya, misalnya disertakan dengan keterangan “diambil berurutan”, maka harus dikerjakan dalam rumus permutasi. Sementara, jika diminta untuk mengambil secara acak dan tidak memperhatikan urutan maka kerjakan dengan menggunakan rumus kombinasi.
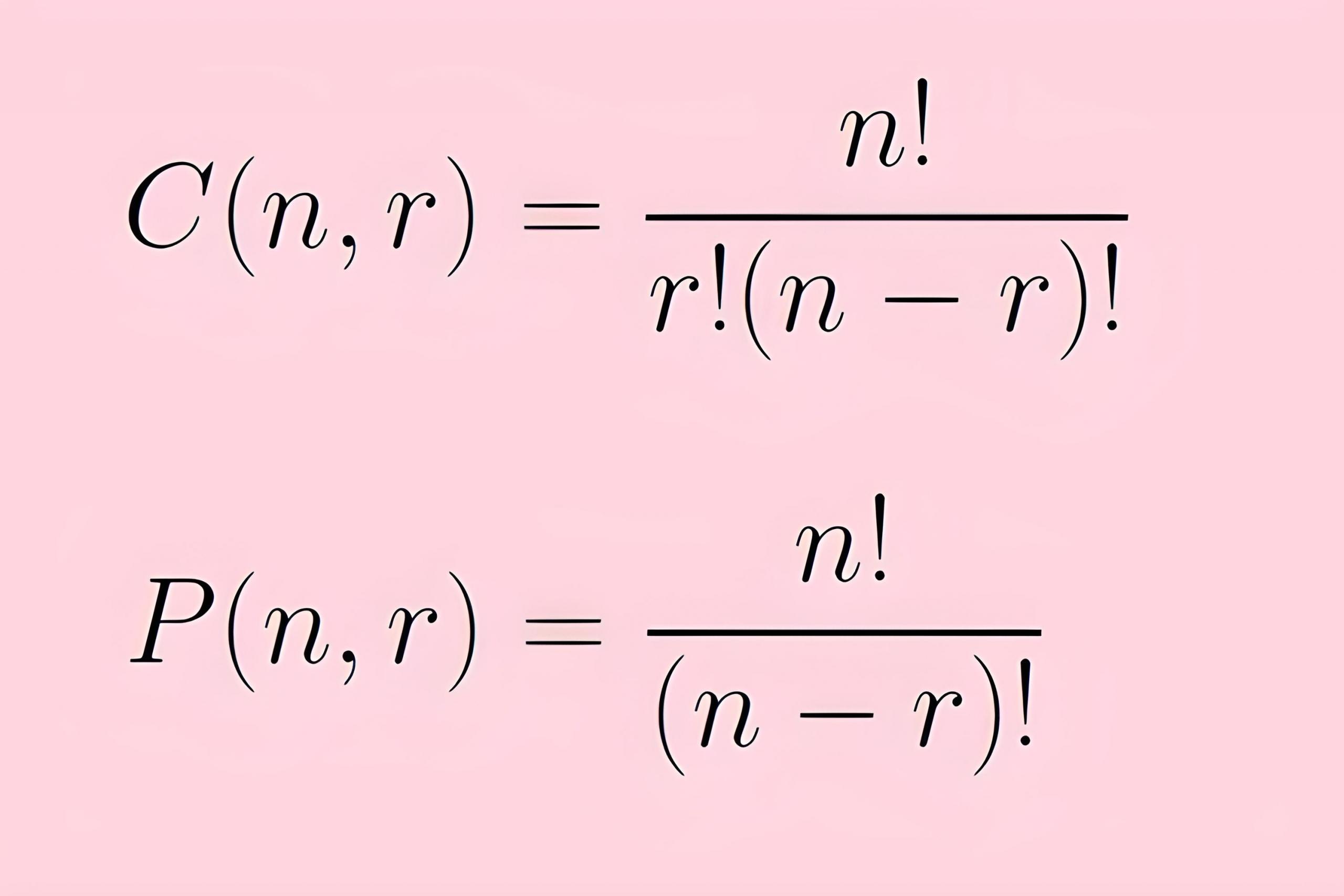
Temukan contoh soal permutasi dan kombinasi, kemudian diskusikan dalam kolom komentar!
Dan jika kalian ingin tahu tentang materi persamaan lingkaran, silahkan klik disini!
Frekuensi Harapan Suatu Kejadian
Dalam materi peluang, Anda juga akan mempelajari tentang frekuensi harapan. Frekuensi harapan pada suatu percobaan adalah harapan banyaknya kejadian yang dapat terjadi dari banyak percobaan yang dilakukan. Frekuensi harapan disimbolkan dengan Fh(A) atau disebut juga sebagai ekspektasi suatu kejadian.
Rumus frekuensi harapan suatu kejadian dapat dituliskan sebagai berikut;
Fh(A) = n x P(A)
Contoh soal!
Sebuah dadu dilempar sebanyak 24 kali. Jika A adalah kejadian munculnya mata dadu prima, maka tentukanlah frekuensi harapan munculnya kejadian A!
Diketahui:
- Banyak percobaan atau n = 24
- A adalah munculnya mata dadu prima, maka A = {2,3,5}, n(A) = 3
- Untuk ruang sampelnya: S = {1,2,3,4,5,6}, maka n(S) = 6
Maka, tentukan terlebih dahulu peluang kejadian A;
P(A) = n(A)/n(S)
P(A) = 3/6 = 1/2
Jadi frekuensi harapannya adalah ;
Fh(A) = n x P(A)
Fh(A) = 24 x ½ = 12
Jadi, apakah Anda sudah memahami materi peluang? Ada banyak contoh soal lainnya yang dapat Anda kerjakan terkait menentukan penyelesaian peluang.
Namun, Jika Anda kesusahan untuk menguasai berbagai konsep peluang, seperti rumus sampel, rumus probabilitas, rumus kombinasi peluang, dan lainnya, maka bergabung dengan Superprof adalah pilihan yang tepat. Di Superprof, Anda dapat menemukan guru-guru berpengalaman yang siap membantu Anda memahami teori peluang dengan lebih mendalam.
Jadi, tunggu apa lagi? Tingkatkan pemahaman matematika Anda dengan bantuan guru dari Superprof!
Anda juga bisa mempelajari tentang fungsi invers di artikel Kami lainnya. Selamat belajar!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
