Dalam dunia matematika, konsep transformasi geometri merupakan salah satu topik yang menarik. Salah satu jenis transformasi geometri yang sering dipelajari di tingkat sekolah, khususnya kelas 9, adalah dilatasi. Pada artikel ini, kita akan membahas secara mendalam tentang rumus dilatasi, pengertian, sifat-sifat, dan tentunya memberikan contoh soal serta pembahasannya. Simak sampai habis untuk memahami rumus dilatasi matematika dengan baik!
Cek di sini jika sedang mencari les matematika di bandung

Pengertian Dilatasi
Ditalasi adalah suatu transformasi yang mengubah ukuran suatu bangun geometri tanpa mengubah bentuk aslinya. Dengan kata lain, dilatasi bisa membuat suatu bangun diperbesar atau diperkecil ukurannya, namun bentuk bangun tersebut tetap sama. Ini berbeda dengan jenis transformasi geometri lainnya, seperti translasi (pergeseran), refleksi (pencerminan), atau rotasi (pemutaran) yang lebih berfokus pada perubahan posisi atau arah suatu bangun, bukan ukuran.
Dalam dilatasi, terdapat dua elemen penting, yaitu:
- Titik pusat dilatasi, yang merupakan titik acuan tempat bangun diperbesar atau diperkecil.
- Faktor skala (k), yang menentukan seberapa besar bangun diperbesar atau diperkecil.
Jika faktor skala lebih besar dari 1, bangun akan diperbesar, sedangkan jika faktor skala antara 0 dan 1, bangun akan diperkecil. Faktor skala juga bisa negatif, yang berarti selain memperbesar atau memperkecil, bangun juga akan terpantul atau terbalik terhadap pusat dilatasi.
Periksa di sini jika kamu ingin mempelajari fungsi kuadrat

Rumus Dilatasi
Sebelum melangkah ke contoh soal, mari kita pahami rumus dilatasi. Rumus dilatasi secara umum terbagi menjadi dua, yaitu dilatasi dengan pusat di titik asal (0, 0) dan dilatasi dengan pusat di titik sembarang (a, b).
1. Dilatasi dengan Pusat O (0, 0)
Untuk dilatasi dengan pusat di titik asal (0,0), rumusnya cukup sederhana. Jika titik P(x, y) didilatasikan dengan faktor skala k terhadap pusat O (0,0), maka koordinat bayangannya, yang kita sebut sebagai P'(x', y'), dapat dihitung dengan rumus berikut:
Rumus Dilatasi:
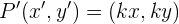
Dengan kata lain, kita hanya perlu mengalikan setiap koordinat x dan y dari titik P dengan faktor skala k.
2. Dilatasi dengan Pusat di Titik Sembarang M (a, b)
Jika titik P(x, y) didilatasikan dengan pusat yang tidak berada di titik asal, misalnya M(a, b), maka rumus dilatasi sedikit lebih kompleks. Rumusnya adalah sebagai berikut:
Rumus Dilatasi:
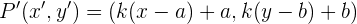
Artinya, kita harus menghitung selisih antara koordinat titik P dengan titik pusat M, kemudian mengalikannya dengan faktor skala k, dan menambahkan kembali koordinat pusat M.
Sifat-Sifat Dilatasi
Selain memahami rumus dilatasi, penting juga untuk memahami sifat-sifat dari dilatasi. Sifat-sifat ini akan mempermudah dalam memprediksi perubahan pada suatu bangun geometri setelah mengalami dilatasi. Berikut adalah sifat-sifat utama dilatasi berdasarkan nilai faktor skala k:
- Jika k > 1, bangun akan diperbesar dan terletak searah terhadap pusat dilatasi dan bangun semula.
- Jika 0 < k < 1, bangun akan diperkecil dan tetap terletak searah terhadap pusat dilatasi dan bangun semula.
- Jika k = 1, bangun tidak mengalami perubahan ukuran, sehingga bangun hasil dilatasi identik dengan bangun asli.
- Jika -1 < k < 0, bangun akan diperkecil, namun bayangan bangun terletak berlawanan arah dengan pusat dilatasi dan bangun semula.
- Jika k = -1, bangun tidak mengalami perubahan ukuran, namun bayangan bangun terletak berlawanan arah dengan bangun semula.
- Jika k < -1, bangun akan diperbesar dan terletak berlawanan arah terhadap pusat dilatasi.
Pelajari juga materi jangkauan antar kuartil
Contoh Dilatasi dan Pembahasannya
Agar lebih memahami konsep dilatasi dan penerapan dilatasi rumus dalam soal matematika, berikut ini beberapa contoh soal dilatasi yang bisa membantu anda dalam belajar.
Contoh Dilatasi 1: Dilatasi dengan Pusat O (0,0)
Tentukan bayangan titik P(3, 4) jika didilatasikan dengan faktor skala k = 2 terhadap pusat O(0,0).
Pembahasan:
Gunakan rumus dilatasi untuk pusat di titik asal:
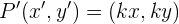
Karena k = 2, maka:
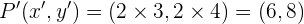
Jadi, bayangan titik P(3, 4) adalah P'(6, 8).
Contoh Dilatasi 2: Dilatasi dengan Pusat di Titik Sembarang
Titik Q(5, -2) didilatasikan dengan faktor skala k = 3 terhadap pusat M(1, 1). Tentukan koordinat bayangan titik Q.
Pembahasan:
Gunakan rumus dilatasi dengan pusat di titik sembarang:
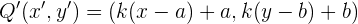
Substitusi nilai-nilai yang diketahui (k = 3, a = 1, b = 1, x = 5, y = -2):
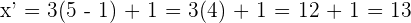
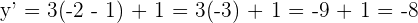
Jadi, bayangan titik Q(5, -2) adalah Q'(13, -8).
Cek di sini jika ingin mempelajari metode horner pada matematika
Contoh Dilatasi 3: Dilatasi dengan Faktor Skala Negatif
Titik R(-4, 6) didilatasikan dengan faktor skala k = -1/2 terhadap pusat O(0,0). Tentukan bayangan titik R.
Pembahasan:
Gunakan rumus dilatasi untuk pusat di titik asal:
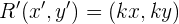
Karena k = -1/2, maka:
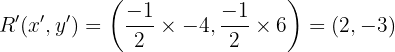
Jadi, bayangan titik R(-4, 6) adalah R'(2, -3).
Melalui pembahasan ini, kita telah mempelajari rumus dilatasi dalam matematika beserta konsep dasar, sifat-sifat, dan penerapannya dalam berbagai contoh soal. Dilatasi merupakan salah satu transformasi geometri yang sering dipelajari di sekolah, khususnya pada pelajaran matematika kelas 9, di mana bangun geometri diperbesar atau diperkecil dengan menggunakan faktor skala tertentu.
Dengan pemahaman yang baik tentang dilatasi dan rumus dilatasi ini, anda dapat lebih mudah menyelesaikan soal-soal matematika terkait dilatasi, baik itu di tingkat sekolah menengah maupun dalam ujian-ujian matematika. Namun, apabila anda masih kesulitan dalam belajar tentang materi rumus dilatasi kelas 9 ini, ada baiknya anda belajar Bersama tutor privat dari Superprof!
Ringkaskan dengan AI