Di sekolah menengah, Anda tentu pernah belajar tentang barisan dan deret. Jika sebelumnya Anda sudah pernah mengenal barisan dan deret aritmetika, kini saatnya Anda mengingat kembali materi barisan dan deret geometri. Apa perbedaan antara barisan geometri dan deret geometri? Bagaimana cara menghitungnya?
Eitt, jangan khawatir. Kita akan menemukan jawabannya di artikel ini. Di artikel ini, kita akan membahas mulai dari pengertian barisan dan deret geometri matematika, rumus geometri, hingga contoh soal untuk menerapkan rumus-rumus tersebut. Yuk, simak penjelasan selengkapnya berikut ini!
Anda bisa mengikuti kursus di tempat les olimpiade matematika sekarang!
Apa Yang Dimaksud Dengan Barisan Geometri?
Barisan geometri adalah pola bilangan yang memiliki rasio tetap antar sukunya. Artinya, setiap suku dalam barisan diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang disebut rasio (r).
Contoh barisan geometri:
1, 2, 4, 8, 16, ...
Di sini, kita dapat melihat bahwa setiap suku diperoleh dengan mengalikan suku sebelumnya dengan 2 (rasio r = 2). Karena rasio antar suku-sukunya tetap (r = 2), maka barisan ini merupakan barisan geometri.
Rumus Nilai Suku Ke-n Dalam Barisan Geometri
Untuk mengetahui suku ke-n dalam barisan geometri, kita dapat menggunakan rumus un:
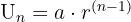
Di mana:
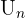adalah suku ke-n yang ingin dicari,- a adalah suku pertama,
- r adalah rasio antar suku, dan
- n adalah urutan suku yang dicari.
Contoh:
Misalnya kita memiliki barisan geometri 1, 3, 9, 27, ... dan kita ingin mencari suku ke-5, dengan a = 1 dan r = 3. Maka:
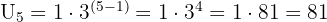
Jadi, suku ke-5 dari barisan ini adalah 81.
Rumus Rasio Barisan Geometri
Untuk menemukan rasio r antara dua suku berturut-turut, kita dapat menggunakan rumus:
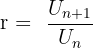
Di mana:
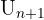adalah suku ke-(n+1), dan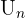- adalah suku ke-n.
Contoh:
Pada barisan geometri 2, 6, 18, 54, ..., kita dapat menghitung rasio antara suku kedua dan pertama:
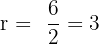
Jadi, rasio barisan ini adalah 3.
Apa perbedaannya dengan rumus determinan matriks?
Apa Itu Deret Geometri?
Deret geometri adalah penjumlahan dari suku-suku dalam barisan geometri. Berbeda dengan barisan geometri yang hanya berupa urutan bilangan, deret geometri melibatkan jumlah seluruh suku yang ada.
Misalnya, deret geometri dari barisan 1, 3, 9, 27, ... adalah:
1+3+9+27+...1 + 3 + 9 + 27 + ...
Deret ini bisa dihitung menggunakan rumus tertentu, tergantung pada apakah deret tersebut terbatas atau tak terbatas.
Rumus Deret Geometri
Jika deret geometri memiliki jumlah suku yang terbatas (hingga n suku), maka rumus sn untuk menghitung jumlah n suku pertama adalah sebagai berikut:
- Jika rasio r < 1:
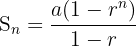
- Jika rasio r>1r > 1:
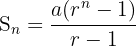
Di mana:
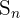adalah jumlah n suku pertama,- a adalah suku pertama,
- r adalah rasio, dan
- n adalah jumlah suku yang ingin dijumlahkan.
Deret Geometri Tak Hingga
Deret geometri tak hingga adalah deret yang memiliki jumlah tak terbatas. Dalam hal ini, jumlahnya akan terus bertambah tanpa batas jika rasio lebih besar dari 1, atau bisa mencapai nilai tertentu jika rasio kurang dari 1.
Ada dua jenis deret geometri tak hingga:
- Deret Geometri Tak Hingga Divergen:
Deret ini terjadi ketika rasio lebih besar dari 1 (r > 1), yang berarti nilai deret akan terus membesar dan tidak memiliki batas.
Misalnya, deret 1 + 2 + 4 + 8 + ... akan terus bertambah tanpa batas. - Deret Geometri Tak Hingga Konvergen:
Deret ini terjadi ketika rasio berada di antara -1 dan 1 (|r| < 1). Dalam hal ini, nilai deret akan semakin mendekati 0, dan jumlahnya dapat dihitung. Rumus deret tak hingga konvergen adalah:
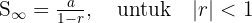
Contoh:
Deret geometri tak hingga konvergen dengan a = 1 dan r = 
:
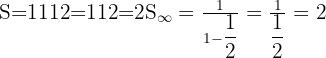
Jadi, jumlah deret geometri tak hingga ini adalah 2.
Lalu bagaimana dengan rumus trigonometri?
Contoh Soal Barisan dan Deret Geometri
Setelah mempelajari perbedaan deret dan barisan geometri serta rumus-rumusnya, ada baiknya Anda juga mempelajari penerapan rumusnya dalam soal barisan geometri berikut ini agar lebih paham.
- Contoh Soal Barisan Geometri
Diberikan barisan geometri 3, 6, 12, 24, ..., tentukan suku ke-6.
Jawaban:- a = 3, r = 2
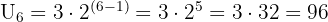
Jadi, suku ke-6 adalah 96.
- Soal Deret Geometri
Diberikan deret geometri 1 + 2 + 4 + 8 + 16, tentukan jumlah 5 suku pertama.
Jawaban:- a = 1, r = 2, n = 5
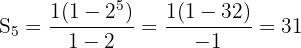
Jadi, jumlah 5 suku pertama adalah 31.
- Soal Barisan Geometri
Tentukan rasio barisan geometri 5, 10, 20, 40, ...
Jawaban: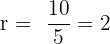
Jadi, rasio barisan ini adalah 2.
- Soal Deret Geometri Tak Hingga
Tentukan jumlah deret geometri tak hingga 1 + 1/2 + 1/4 + 1/8 + ...
Jawaban:- a = 1, r = 1/2
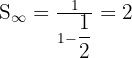
Jadi, jumlah deret geometri tak hingga ini adalah 2.
- Contoh Soal Geometri: Deret Geometri
Diberikan deret geometri 3 + 6 + 12 + 24 + ..., tentukan jumlah 4 suku pertama.
Jawaban:- a = 3, r = 2, n = 4
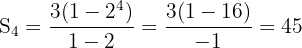
Jadi, jumlah 4 suku pertama adalah 45.
Masih Bingung? Minta Bantuan Guru Superprof Aja!
Jika setelah membaca penjelasan ini Anda masih merasa bingung atau ingin memperdalam pemahaman tentang barisan dan deret matematika dan geometri, Anda bisa mencari bantuan dari guru privat yang berpengalaman. Di Superprof, Anda bisa menemukan berbagai guru matematika yang siap membantu Anda mempelajari deret aritmatika dan geometri dengan cara yang mudah dipahami. Belajar matematika bisa lebih menyenangkan dengan bimbingan yang tepat. Jadi, tunggu apa lagi? Cari guru privat matematika terbaik di Superprof dan raih pemahaman yang lebih dalam mengenai aritmatika dan geometri.
Anda juga bisa memeriksa artikel-artikel kami lainnya tentang logika matematika di website Superprof.
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
