Permutasi dan kombinasi merupakan dua konsep yang sering digunakan di teori peluang dalam menghitung jumlah susunan atau kombinasi elemen dari himpunan. Seringnya, siswa bingung saat disuruh membedakan keduanya. Salah satu perbedaan utama antara permutasi dan kombinasi terletak pada urutan elemen. Dalam permutasi, urutan sangat diperhatikan, sementara dalam kombinasi, urutan tidak memengaruhi hasil akhir.
Permutasi digunakan ketika urutan elemen sangat penting. Sebaliknya, kombinasi digunakan ketika urutan elemen tidak berpengaruh pada hasil. Untuk lebih memahami hal ini, perhatikan contoh berikut. Pada babak penyisihan sebuah lomba, pemilihan 5 peserta terbaik untuk maju ke babak final adalah kombinasi, karena urutan peserta tidak penting. Namun, pada babak final, pemilihan juara 1, juara 2, dan juara 3, di mana urutan sangat penting, merupakan contoh permutasi.
Penasaran bagaimana cara menghitung jumlah susunan dalam permutasi dan kombinasi? Simak penjelasan lebih lanjut dalam artikel ini! Jika kamu ingin belajar lebih terstruktur, kamu juga bisa mengikuti kursus matematika untuk memperkuat pemahamanmu.

Pengertian Permutasi dan Kombinasi
Apa itu Permutasi?
Permutasi merupakan cara menyusun atau mengatur elemen-elemen dari himpunan dengan memperhatikan urutannya. Dalam perhitungan permutasi, urutan sangatlah penting. Jika urutan diubah, maka hasilnya akan dianggap berbeda.
Ada banyak jenis permutasi yang perlu kamu tahu. Permutasi dengan pengulangan membuat besar kemungkinan elemen yang sama akan muncul lebih dari satu kali, berbeda dengan permutasi yang tanpa pengulangan dan hanya memperbolehkan setiap elemen muncul satu kali dalam susunan yang dihasilkan. Contohnya seperti, PIN gawai yang termasuk contoh permutasi dengan pengulangan, sedangkan di perlombaan apapun, urutan pemenang yang diumumkan merupakan contoh permutasi tanpa pengulangan.
Apa itu Kombinasi?
Kombinasi merupakan cara memilih elemen dari himpunan tanpa memperhatikan urutan. Dalam kombinasi, hanya jumlah elemen yang penting dipilih, urutannya tidak berpengaruh. Kombinasi bisa terjadi dengan atau tanpa pengulangan, tergantung pada jenis masalah yang dihadapi.
Kombinasi juga terbagi menjadi dua jenis:
1. Pengulangan diperbolehkan: Contoh, logika saat mengambil 3 bola dari wadah yang berisi 3 bola merah dan 3 bola biru, bisa saja terambil 2 bola merah dan 1 bola biru.
2. Pengulangan tidak diperbolehkan: Contoh lainnya seperti halnya pemilihan 2 orang dari 5 orang dalam kelompok. Tidak mungkin dua pilihan tadi berasal dari orang yang sama.
Setelah memahami pengertian dari permutasi dan kombinasi, apa kamu sudah tau perbedaan mendasarnya? Berikut lebih jelasnya!
Jenis-Jenis Permutasi

Terdapat beberapa jenis-jenis permutasi yang harus kamu ketahui. Kita bahas satu per satu!
1. Permutasi dari n Elemen
Permutasi dari n elemen merupakan jenis permutasi yang paling sederhana. Di sinilah, semua elemen dari himpunan akan disusun dalam urutan. Berikut permutasi rumus untuk jenis ini
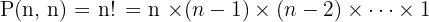
Contoh:
Misalnya, dalam sebuah lomba, panitia memutuskan untuk memilih 4 pemenang dari 8 peserta yang ikut serta. Setiap posisi pemenang, seperti juara 1, juara 2, juara 3, dan juara harapan 1, memiliki urutan yang berbeda. Nah, berapa banyak cara yang bisa dilakukan untuk menyusun keempat pemenang tersebut?
Jawaban:
Karena urutan posisi pemenang sangat diperhatikan, maka ini termasuk dalam permutasi. Dengan 8 peserta yang ada, di mana kita memilih 4 pemenang, maka kita bisa menggunakan rumus permutasi untuk menghitung jumlah cara yang bisa dilakukan untuk menyusun keempat pemenang tersebut.
Rumus permutasi:
P(n, r) = n! / (n - r)!
P(8, 4) = 8! / (8 - 4)! = 8 × 7 × 6 × 5 = 1680 cara.
Jadi, ada 1680 cara untuk menyusun 4 pemenang dari 8 peserta.
2. Permutasi n Elemen yang Diambil r Elemen
Permutasi ini digunakan ketika kita hanya memilih sebagian elemen dari himpunan yang ada. Misalnya, jika kamu memilih 3 orang dari 5 orang untuk membentuk sebuah tim, maka urutan posisi mereka tetap diperhitungkan. Rumusnya juga menggunakan :
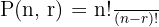
3. Permutasi dengan Unsur yang Sama
Kadang-kadang dalam suatu himpunan terdapat elemen yang identik. Misalnya, dalam kata "AAB", ada dua huruf "A" yang sama. Dalam kasus seperti ini, kita perlu menggunakan rumus permutasi unsur yang sama untuk menghitung jumlah susunan yang mungkin. Rumusnya seperti berikut :
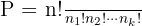
Keterangan:
n = jumlah total elemen
k1 = jumlah elemen dalam kelompok 1 yang identik
k2 = jumlah elemen dalam kelompok 2 yang identik
…
kt = jumlah elemen dalam kelompok kt yang identik
Di mana t = 1, 2, 3, …
4. Permutasi Siklis
Permutasi siklis melibatkan susunan elemen luas dalam bentuk lingkaran. Misalnya, jika ada 6 orang yang duduk mengelilingi meja bundar, maka jumlah cara untuk mengatur tempat duduk mereka adalah 5! (bukan 6!), karena posisi relatif antar oranglah yang penting, bukan posisi absolut mereka.
Contoh:
Misalnya, ada 6 teman yang akan duduk bersama mengelilingi sebuah meja bundar dalam sebuah acara makan malam. Nah, berapa banyak cara yang bisa dilakukan untuk menyusun posisi duduk mereka?
Jawaban:
Dengan jumlah orang (n) = 6, maka:
Rumus permutasi siklis: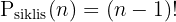
6P_siklis = (6 - 1)! = 5! = 5 × 4 × 3 × 2 × 1 = 120 cara.
Jadi, ada 120 cara yang dapat dilakukan untuk menyusun posisi duduk 6 teman tersebut dalam sebuah meja bundar.
5. Permutasi dengan Pengulangan
Pada jenis permutasi ini, elemen yang sama boleh muncul lebih dari satu kali dalam susunan yang terbentuk. Ini sering digunakan untuk menghitung susunan angka atau huruf yang sama, seperti dalam kasus PIN atau kode sandi. Misalnya, jika kita menyusun angka 3 digit dari angka 1 sampai 6, dengan permutasi dengan pengulangan, kita bisa mendapatkan susunan seperti 111, 222, dan seterusnya.
Berikut rumusnya : 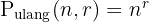
Contoh:
Misalnya, berapa banyak kemungkinan susunan angka 3 digit yang bisa dibentuk menggunakan angka 1, 2, 3, 4, 5, dan 6.
Penerapan Permutasi dalam Kehidupan Sehari-Hari

Meskipun terdengar rumit, permutasi banyak digunakan dalam kehidupan sehari-hari. Misalnya, dalam dunia perbankan, kita menggunakan permute untuk menghitung bunga majemuk atau menentukan lama waktu pinjaman. Dalam bidang kebumian, skala logaritmik yang melibatkan konsep permuta digunakan untuk mengukur kekuatan gempa. Bahkan dalam pengaturan sifat acara, seperti lomba atau acara makan malam, permutasi digunakan untuk menentukan siapa yang duduk di posisi mana.
Dalam dunia teknologi dan bisnis, perhitungan permutasi tidak kalah bermanfaat, seperti saat mengatur urutan produksi atau perhitungan peluang dalam algoritma tertentu. Jika kamu ingin belajar fleksibel dari rumah, kamu bisa mencoba kursus matematika online untuk membahas materi dan latihan soal secara lebih mendalam.
Kesimpulan
Secara keseluruhan, permutasi adalah konsep yang sangat penting dalam teori peluang yang membantu kita menghitung jumlah susunan elemen dengan memperhatikan urutan. Dengan memahami jenis-jenis permutasi, seperti permutasi siklis, permutasi dengan unsur yang sama, dan permutasi dengan pengulangan, kamu akan lebih mudah menyelesaikan berbagai soal matematika yang melibatkan susunan dan pengaturan elemen. Dengan rumus yang tepat, kamu bisa menghitung kemungkinan yang ada dengan lebih efisien. Untuk memahami konsep-konsep ini lebih dalam, jangan khawatir!
Bergabunglah dengan kelas privat Superprof, di mana kamu bisa belajar langsung dengan pengajar ahli yang akan membimbingmu secara personal. Kamu bisa dapat penjelasan yang lebih mendalam, latihan soal, dan tips-tips jitu agar pemahamanmu semakin mantap. Daftarkan dirimu di Superprof sekarang juga dan raih pengalaman belajar menyenangkan dalam pelajaran matematika!
Ringkaskan dengan AI















