FBP dan KPK adalah mtk konsep dasar yang sering kita temui, terutama saat mempelajari bilangan bulat. Konsep ini sangat penting karena memiliki banyak penerapan, seperti dalam pembagian barang secara merata, penjadwalan, atau dalam mencari ukuran yang tepat dalam pengolahan data.
Dalam artikel ini, kita akan membahas tentang cara mencari KPK (Kelipatan Persekutuan Terkecil) dan FPB (Faktor Persekutuan Terbesar) dengan menggunakan metode yang tepat. Pahami dengan seksama setiap langkahnya, dan kamu akan bisa mengerjakan soal KPK dan FPB kelas 5 dengan mudah.
Cek disini untuk les privat matematika di Surabaya

KPK Matematika

KPK (Kelipatan Persekutuan Terkecil) adalah bilangan bulat positif terkecil yang dapat dibagi habis oleh dua bilangan atau lebih. KPK memiliki banyak kegunaan. Misalnya, ketika kita ingin mencari waktu yang bersamaan untuk dua kegiatan yang berlangsung dalam periode waktu tertentu, kita bisa menggunakan konsep KPK untuk menemukan waktu yang paling tepat.
Untuk lebih memahami KPK, mari kita lihat contoh berikut:
KPK dari 12 dan 15
- Kelipatan 12 adalah 12, 24, 36, 48, 60, 72, ...
- Kelipatan 15 adalah 15, 30, 45, 60, 75, ...
Dari kelipatan 12 dan 15 di atas, yang terkecil dan sama di antara kedua daftar kelipatan tersebut adalah 60. Maka, KPK dari 12 dan 15 adalah 60.
Cara Menghitung KPK
Ada dua cara untuk menghitung KPK, yaitu dengan menggunakan faktorisasi prima dan menentukan kelipatan angka terkecil yang sama. Di bawah ini akan dijelaskan lebih detail tentang kedua cara tersebut.
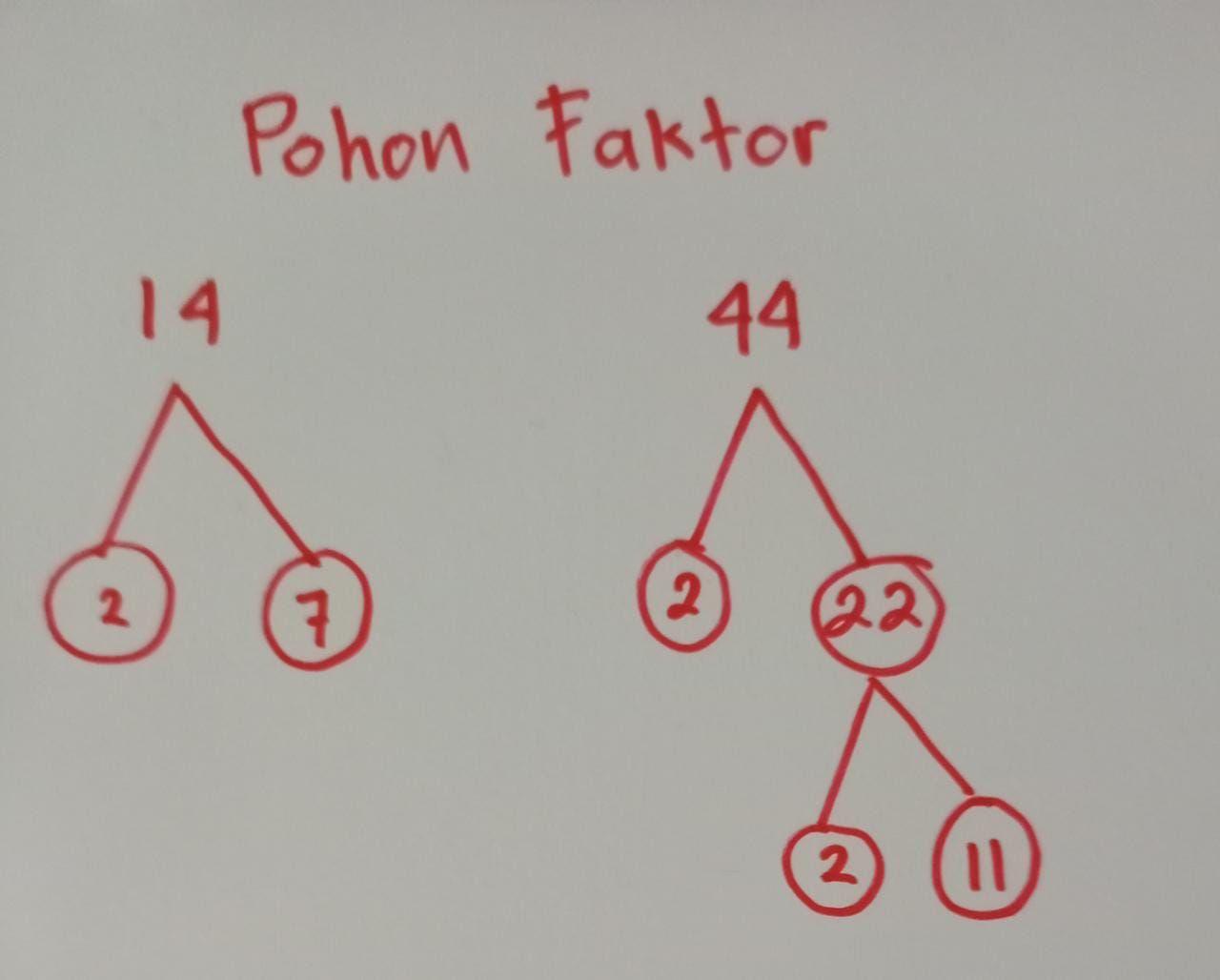
Faktorisasi (Pohon Faktor)
Cara mengerjakan KPK yang pertama adalah dengan faktorisasi prima menggunakan pohon faktor. Metode ini melibatkan proses pemecahan angka menjadi faktor-faktor primanya. Dengan pohon faktor, kita bisa menggambarkan pembagian angka hingga menjadi bilangan prima.
Langkah-langkah:
- Faktorkan setiap bilangan menjadi bilangan prima.
- Ambil semua faktor prima yang ada, dan pastikan untuk memilih faktor dengan pangkat terbesar jika faktor tersebut muncul lebih dari sekali.
- Kalikan semua faktor prima yang sudah diambil.
Contoh:
Cari KPK dari 48 dan 60.
- Faktorisasi prima dari 48:
| 48 | |
| 2 | 24 |
| 2 | 12 |
| 2 | 6 |
| 2 | 3 |
| 3 | 1 |
Sehingga faktorisasi prima dari 48 adalah 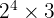 .
.
- Faktorisasi prima dari 60:
| 60 | |
| 2 | 30 |
| 2 | 15 |
| 3 | 5 |
| 5 | 1 |
Sehingga faktorisasi prima dari 60 adalah 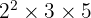 .
.
Sekarang kita ambil semua faktor prima dari kedua bilangan. Faktor-faktor dari 48 adalah 2^4 dan 3, sementara faktor-faktor dari 60 adalah 2^2, 3, dan 5. Untuk KPK, kita ambil faktor dengan pangkat terbesar, yaitu  , 3, dan 5.
, 3, dan 5.
Sehingga, KPK dari 48 dan 60 adalah:
KPK = 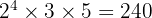
Menentukan Kelipatan Angka Terkecil yang Sama
Cara menentukan KPK yang lainnya adalah dengan menentukan kelipatan angka terkecil yang sama. Metode ini sederhana namun kurang efisien untuk bilangan besar. Caranya adalah dengan menulis beberapa kelipatan dari masing-masing bilangan dan mencari yang terkecil di antara keduanya.
Contoh:
Tentukan KPK dari 4 dan 6.
- Kelipatan 4: 4, 8, 12, 16, 20, 24...
- Kelipatan 6: 6, 12, 18, 24...
Kelipatan terkecil yang sama adalah 12. Jadi, KPK dari 4 dan 6 adalah 12.
Mudah bukan memahami pengertian KPK? Ikuti tulisan Kami lainnya untuk mempelajari tentang pengertian eksponen!

FPB
FPB (Faktor Persekutuan Besar) adalah bilangan bulat positif terbesar yang dapat membagi habis dua bilangan atau lebih tanpa sisa. Dalam banyak hal, FPB digunakan untuk menentukan pembagian terbesar yang bisa dilakukan antara dua atau lebih bilangan. Misalnya, jika kita memiliki dua kelompok barang yang ingin dibagi ke dalam wadah dengan ukuran terbesar yang sama, kita perlu mencari FPB dari ukuran kedua kelompok tersebut.
Misalnya, jika kita ingin membagi 20 dan 30 menjadi bagian yang lebih kecil dengan ukuran yang sama, kita mencari FPB untuk mengetahui ukuran terbesar dari bagian-bagian yang lebih kecil. Dengan menggunakan FPB, kita dapat memastikan bahwa pembagian tersebut dilakukan secara maksimal tanpa sisa.
Menurut kalian apakah deretan angka dan kelipatannya dapat dikatakan sebagai pola bilangan?
Cara Menghitung FPB
Ada beberapa cara untuk menghitung FPB, dan cara-cara ini sangat bergantung pada bilangan yang sedang dihitung. Cara yang paling umum digunakan adalah dengan menggunakan faktorisasi prima. Di bawah ini adalah penjelasan lengkap mengenai beberapa cara mencari FPB.
Faktorisasi (Pohon Faktor)
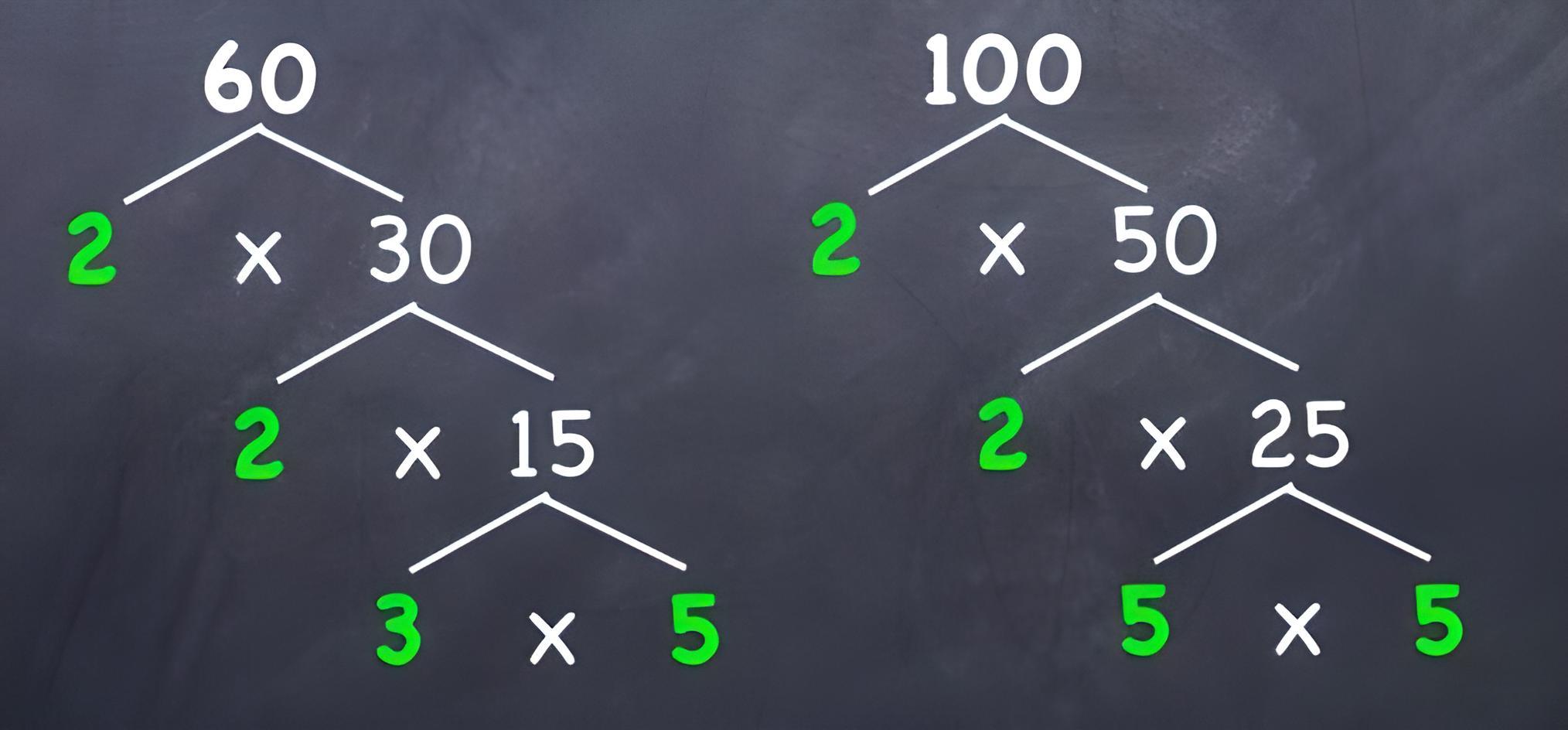
Hampir mirip dengan mencari KPK, FPB juga dapat dicari menggunakan metode pohon faktor. Metode ini melibatkan pemecahan bilangan menjadi faktor-faktor primanya. Setelah bilangan dibagi menjadi faktor-faktor prima, kita akan mencari faktor yang sama dari kedua bilangan dan memilih yang terkecil.
Langkah-langkah:
- Faktorkan setiap bilangan menjadi bilangan prima.
- Ambil semua faktor prima yang sama dari kedua bilangan.
- Pilih faktor dengan pangkat terkecil jika faktor tersebut muncul lebih dari sekali.
- Kalikan faktor-faktor yang sama untuk mendapatkan FPB.
Contoh:
Tentukan FPB dari 18 dan 30.
- Faktorisasi prima dari 18:
| 18 | |
| 2 | 9 |
| 3 | 3 |
| 3 | 1 |
Sehingga faktorisasi prima dari 18 adalah 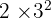 .
.
- Faktorisasi prima dari 30:
| 30 | |
| 2 | 15 |
| 3 | 5 |
| 5 | 1 |
Sehingga faktorisasi prima dari 30 adalah 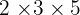 .
.
Sekarang kita ambil semua faktor yang sama dari kedua bilangan. Faktor yang sama antara 18 dan 30 adalah 2 dan 3. Untuk FPB, kita pilih faktor dengan pangkat terkecil, yaitu 2 dan 3.
Sehingga, FPB dari 18 dan 30 adalah:
FPB = 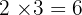
Mengambil Angka Yang Sama Dan Terbesar Dari Faktor Persekutuan
Metode kedua untuk menghitung FPB adalah dengan mengambil angka yang sama dan terbesar dari faktor persekutuan. Ini lebih cepat dilakukan karena kita hanya perlu mencari faktor-faktor yang dapat membagi kedua bilangan dan memilih faktor terbesar dari faktor-faktor yang ada.
Langkah-langkah:
- Tentukan faktor-faktor dari kedua bilangan.
- Identifikasi faktor yang sama antara kedua bilangan.
- Pilih faktor yang terbesar dari faktor yang sama.
Contoh:
Cari FPB dari 20 dan 30.
- Faktor-faktor dari 20: 1, 2, 4, 5, 10, 20
- Faktor-faktor dari 30: 1, 2, 3, 5, 6, 10, 15, 30
Faktor yang sama antara 20 dan 30 adalah 1, 2, 5, dan 10. Faktor terbesar yang sama adalah 10.
Jadi, FPB dari 20 dan 30 adalah 10.
Metode ini lebih sederhana dan cocok digunakan untuk bilangan yang tidak terlalu besar.
Jika kamu ingin memperkuat pemahaman materi ini lewat pendampingan rutin, kamu bisa mencari les matematika smp terdekat sesuai kebutuhan belajarmu.
Tunggu apa lagi untuk les privat matematika di Bandung
Contoh Soal FPB dan KPK Kelas 5

Agar kamu lebih paham bagaimana mengerjakan cara menghitung KPK dan FPB, maka perlu latihan soal. Berikut adalah 10 contoh soal FPB dan KPK kelas 7 lengkap dengan pembahasan, langkah-langkah penyelesaian, dan jawabannya. Setiap contoh soal KPK dan FPB akan disertai dengan pohon faktor untuk memudahkan pemahaman.
Soal 1: Tentukan KPK dan FPB dari 12 dan 30!
Pembahasan:
Faktorisasi 12:
| 30 | |
| 2 | 6 |
| 2 | 3 |
| 3 | 1 |
Jadi faktorisasi angka 12 adalah 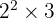
Faktorisasi 30:
| 30 | |
| 2 | 15 |
| 3 | 5 |
| 5 | 1 |
Jadi faktorisasi angka 30 adalah 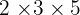
Untuk mencari KPK, kita ambil semua faktor prima dengan pangkat terbesar dari kedua bilangan. Jadi:
KPK = 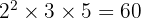
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil dari kedua bilangan. Jadi:
FPB = 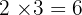
Jawaban:
KPK = 60, FPB = 6
Soal 2: Tentukan KPK dan FPB dari 18 dan 24!
Pembahasan:
Faktorisasi 18:
| 18 | |
| 2 | 9 |
| 3 | 3 |
| 3 | 1 |
Jadi faktorisasi angka 18 adalah 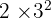
Faktorisasi 24:
| 24 | |
| 2 | 12 |
| 2 | 6 |
| 2 | 3 |
| 3 | 1 |
Jadi faktorisasi angka 24 adalah 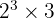
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 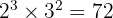
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 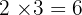
Jawaban:
KPK = 72, FPB = 6
Soal 3: Tentukan KPK dan FPB dari 6 dan 8!
Pembahasan:
Faktorisasi 6:
| 6 | |
| 2 | 3 |
| 3 | 1 |
Jadi faktorisasi angka 6 adalah 
Faktorisasi 8:
| 8 | |
| 2 | 4 |
| 2 | 2 |
| 2 | 1 |
Jadi faktorisasi angka 8 adalah 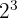
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 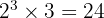
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 2
Jawaban:
KPK = 24, FPB = 2
Soal 4: Tentukan KPK dan FPB dari 15 dan 25!
Pembahasan:
Faktorisasi 15:
| 15 | |
| 3 | 5 |
| 5 | 1 |
Jadi faktorisasi angka 15 adalah 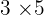
Faktorisasi 25:
| 25 | |
| 5 | 5 |
| 5 | 1 |
Jadi faktorisasi angka 25 adalah 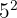
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 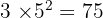
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 5
Jawaban:
KPK = 75, FPB = 5
Referensi lain yang perlu kalian ikuti adalah tentang notasi sigma, kalian akan tertarik untuk membacanya.
Soal 5: Tentukan KPK dan FPB dari 4 dan 10!
Pembahasan:
Faktorisasi 4:
| 4 | |
| 2 | 2 |
| 2 | 1 |
Jadi faktorisasi angka 4 adalah 
Faktorisasi 10:
| 10 | |
| 2 | 5 |
| 5 | 1 |
Jadi faktorisasi angka 10 adalah 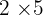
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 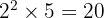
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 2
Jawaban:
KPK = 20, FPB = 2
Soal 6: Tentukan KPK dan FPB dari 8 dan 12!
Pembahasan:
Faktorisasi 8:
| 8 | |
| 2 | 4 |
| 2 | 2 |
| 2 | 1 |
Jadi faktorisasi angka 8 adalah 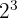
Faktorisasi 12:
| 12 | |
| 2 | 6 |
| 2 | 3 |
| 3 | 1 |
Jadi faktorisasi angka 12 adalah
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 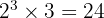
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 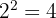
Jawaban:
KPK = 24, FPB = 4
Soal 7: Tentukan KPK dan FPB dari 9 dan 27!
Pembahasan:
Faktorisasi 9:
| 9 | |
| 3 | 3 |
| 3 | 1 |
Jadi faktorisasi angka 9 adalah 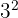
Faktorisasi 27:
| 27 | |
| 3 | 9 |
| 3 | 3 |
| 3 | 1 |
Jadi faktorisasi angka 25 adalah 
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 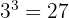
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 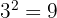
Jawaban:
KPK = 27, FPB = 9
Soal 8: Tentukan KPK dan FPB dari 5 dan 15!
Pembahasan:
Faktorisasi 5:
| 5 | |
| 5 | 1 |
Jadi faktorisasi angka 5 adalah 5
Faktorisasi 15:
| 15 | |
| 3 | 5 |
| 5 | 1 |
Jadi faktorisasi angka 15 adalah 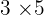
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 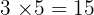
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 5
Jawaban:
KPK = 15, FPB = 5
Soal 9: Tentukan KPK dan FPB dari 14 dan 28!
Pembahasan:
Faktorisasi 14:
| 14 | |
| 2 | 7 |
| 7 | 1 |
Jadi faktorisasi angka 14 adalah 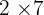
Faktorisasi 28:
| 28 | |
| 2 | 14 |
| 2 | 7 |
| 7 | 1 |
Jadi faktorisasi angka 28 adalah
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 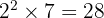
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 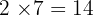
Jawaban:
KPK = 28, FPB = 14
Soal 10: Tentukan KPK dan FPB dari 16 dan 40!
Pembahasan:
Faktorisasi 16:
| 16 | |
| 2 | 8 |
| 2 | 4 |
| 2 | 2 |
| 2 | 1 |
Jadi faktorisasi angka 25 adalah 
Faktorisasi 40:
| 40 | |
| 2 | 20 |
| 2 | 10 |
| 2 | 5 |
| 5 | 1 |
Jadi faktorisasi angka 40 adalah 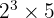
Untuk mencari KPK, kita ambil semua faktor dengan pangkat terbesar:
KPK = 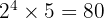
Untuk mencari FPB, kita ambil faktor yang sama dengan pangkat terkecil:
FPB = 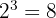
Jawaban:
KPK = 80, FPB = 8
Periksa di sini untuk mengetahui pengertian bilangan berpangkat
Bagaimana? Mudah bukan? Jika kamu masih kesulitan memahami materi di atas, kamu bisa bergabung bersama Superprof. Superprof memberikan sesi pertemuan pertama gratis bagimu! Jangan ragu untuk bergabung dan belajar lebih banyak mengenai konsep matematika dengan bantuan tutor yang berpengalaman. Yuk, mulai belajar sekarang!
Ringkaskan dengan AI