Matematika merupakan mata pelajaran wajib yang memiliki banyak manfaat dalam kehidupan sehari-hari. Lebih dari sekadar bilangan dan perhitungan, konsep matematika banyak membantu pekerjaan sehari-hari dan bidang ilmu lainnya. Itu mengapa, sulit bagi Anda untuk menghindari matematika baik di sekolah maupun dalam kehidupan nyata.
Salah satu materi matematika yang dipelajari saat di bangku SMA adalah limit fungsi aljabar kelas 12. Materi limit fungsi aljabar ini lanjutan dari materi fungsi atau yang umumnya dinyatakan dalam f(x) pada kelas 10.
Fungsi tersebut memiliki variabel yang apabila disubstitusikan dengan suatu bilangan, maka akan menghasilkan nilai tertentu. Sebagai contoh f(x) = 2x + 7 dengan x = 2, maka nilai f(x) = 2.2 + 7 = 11. Lantas bagaimana jika nilainya menghasilkan 0/0? Disinilah kita dapat menggunakan konsep limit matematika.
Cek di sini untuk les matematika di Medan
Jika mengambil contoh sederhana, penerapan materi limit fungsi ini juga sangat dekat dengan keseharian kita. Sebagai contoh saat ibu-ibu rumah tangga yang menakar beras dengan cangkir saat hendak memasak. Jika satu cangkir beras tersebut setara dengan 1/4 kg beras, maka dapat diperkirakan bahwa 4 cangkir beras beratnya mendekati 1 kg beras. Perkiraan pengukuran pendekatan ini dibahas pada materi limit fungsi aljabar.
Yuk simak penjelasan selengkapnya tentang materi limit dan dapatkan daftar guru privat matematika terbaik hanya di Superprof! Untuk memahami materi ini secara menyeluruh, kamu juga bisa bergabung dengan kursus matematika.
Pengertian Fungsi Limit Aljabar
Limit artinya adalah nilai yang didekati oleh suatu fungsi saat variabelnya mendekati suatu angka tertentu. Konsep ini sangat esensial dalam kalkulus, karena banyak fungsi matematika tidak terdefinisikan pada titik tertentu, tetapi kita bisa mengetahui nilai yang mendekatinya ketika variabel fungsi mendekati titik tersebut.
Secara lebih sederhana, limit menggambarkan bagaimana nilai fungsi akan mendekati suatu angka L saat variabel x mendekati titik tertentu a. Oleh karena itu, limit terdiri dari limit kanan dan limit kiri. Limit kiri dan limit kanan memiliki notasi penulisan yang berbeda:
- Limit kanan ditulis dengan notasi:
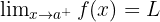
Artinya, fungsi mendekati nilai L saat x mendekati a dari arah kanan (nilai x lebih besar dari a).
- Limit kiri ditulis dengan notasi:
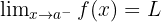
Artinya, fungsi mendekati nilai L saat x mendekati a dari arah kiri (nilai x lebih kecil dari a).
Bentuk Limit
Limit bisa dibedakan menjadi dua bentuk utama, yaitu limit tentu dan limit tak tentu. Keduanya memiliki cara penyelesaian yang berbeda.
Limit Tentu
Limit tentu adalah bentuk limit di mana fungsi mendekati suatu nilai yang terdefinisi dengan baik pada titik tertentu. Ketika kita mencari limit pada titik tertentu dan mendapatkan nilai yang pasti, maka itu adalah limit tentu.
Sebagai contoh limit fungsi f(x) = 2x + 3 saat x mendekati 4, kita cukup mengganti x dengan 4 dan menghitungnya.
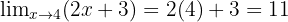
Jadi, nilai limitnya adalah 11.
Limit Tak Tentu
Limit tak tentu adalah ketika fungsi tidak dapat didefinisikan atau memiliki bentuk yang tidak dapat dihitung secara langsung, sering kali menghasilkan bentuk seperti 0/0 atau ∞/∞. Ketika kita menemui bentuk ini, kita perlu menggunakan metode khusus untuk menyelesaikan limit tersebut, seperti faktorisasi atau perkalian sekawan.
Contoh:
Misalnya kita memiliki limit fungsi f(x) = (x² - 4)/(x - 2) saat x mendekati 2. Jika kita coba substitusi nilai x = 2, kita akan mendapatkan 0/0, yang merupakan bentuk tak tentu. Oleh karena itu, kita perlu melakukan pemfaktoran dan menyederhanakan bentuk fungsi tersebut.
Rumus Limit
Secara umum, rumus limit fungsi aljabar dapat ditulis dalam bentuk berikut:
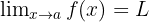
Artinya, ketika nilai x mendekati angka a, fungsi f(x) akan mendekati nilai L. Limit ini menunjukkan bahwa meskipun x tidak mencapai nilai a, kita masih bisa mengetahui nilai fungsi tersebut saat x mendekati a.
Sifat-Sifat Limit
Dalam perhitungan limit, ada beberapa aturan limit yang membantu kita menyelesaikan soal dengan lebih mudah. Berikut adalah beberapa sifat-sifat limit khusus:
- Limit konstanta:
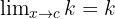Jika suatu fungsi hanya berupa konstanta k, maka limitnya tetap k. Artinya, nilai batas dari suatu angka tetap tidak akan berubah, tidak peduli nilai x mendekati berapa. - Limit identitas:
Jika fungsi adalah variabel itu sendiri, maka limitnya adalah nilai yang didekati oleh variabel tersebut. Misalnya, 
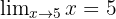, karena nilai x sendiri langsung mendekati angka tersebut. - Limit perkalian konstanta:
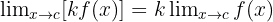Jika suatu fungsi dikalikan dengan konstanta, maka kita bisa menarik konstanta keluar dari limit. Misalnya, 
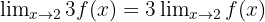. - Limit penjumlahan dan pengurangan:
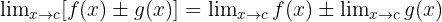Limit dari penjumlahan (atau pengurangan) dua fungsi sama dengan jumlah (atau selisih) dari limit masing-masing fungsi. - Limit perkalian:
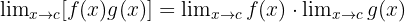Limit dari perkalian dua fungsi sama dengan perkalian dari limit masing-masing fungsi. - Limit pembagian:
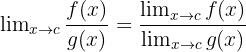dengan syarat limit \lim_{{x \to c}} g(x) \neq 0. - Limit perpangkatan:
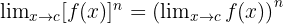Jika fungsi dipangkatkan, maka limitnya juga dipangkatkan dengan eksponen yang sama. - Limit akar:
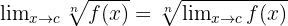Limit dari akar fungsi sama dengan akar dari limit fungsi tersebut.
Bagaimana dengan pengertian baris dan deret aritmatika, apakah kamu sudah memahaminya?
Cara Menyelesaikan Soal Limit
Dalam menyelesaikan soal limit, ada beberapa metode yang bisa digunakan. Beberapa di antaranya adalah substitusi, faktorisasi, dan perkalian sekawan. Setiap metode ini memiliki aplikasi tersendiri tergantung pada bentuk soal yang diberikan.
Substitusi
Metode substitusi adalah metode yang paling sederhana dan sering digunakan dalam menyelesaikan soal limit matematika kelas 12. Jika kita mengganti x dengan nilai tertentu dan hasilnya tidak menghasilkan bentuk tak tentu, maka kita bisa langsung mendapatkan nilai limitnya.
Contoh soal limit aljabar dengan substitusi:
Tentukan limit fungsi f(x) = 2x + 3 saat x mendekati 4:
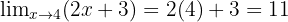
Jadi, nilai limitnya adalah 11.
Namun, jika substitusi menghasilkan bentuk tak tentu seperti 0/0, maka kita perlu menggunakan metode lain.
Klik di sini untuk mengetahui cara pembagian polinomial dalam Matematika!
Limit Pemfaktoran
Jika kita menghadapi soal fungsi limit switch yang menghasilkan bentuk tak tentu, metode yang dapat digunakan adalah faktorisasi. Dalam metode ini, kita akan memfaktorkan fungsi untuk menyederhanakan ekspresi dan menghilangkan faktor yang menyebabkan bentuk tak tentu.
Soal limit aljabar dengan faktorisasi:
Tentukan limit fungsi f(x) = (x² - 4)/(x - 2) saat x mendekati 2.
Pertama, kita substitusi x = 2, namun hasilnya 0/0 (tak tentu).
Sekarang, kita faktorkan x² - 4 menjadi (x - 2)(x + 2):
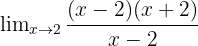
Kita bisa menghilangkan faktor (x - 2) di pembilang dan penyebut:
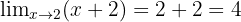
Jadi, nilai limitnya adalah 4.
Perkalian Sekawan
Metode perkalian sekawan digunakan ketika soal limit kelas 12 mengandung bentuk akar yang menyebabkan hasilnya tak tentu. Metode ini mengharuskan kita mengalikan pembilang dan penyebut dengan faktor sekawan dari akar yang ada untuk menghilangkan bentuk tak tentu.
Contoh limit fungsi dengan perkalian sekawan:
Tentukan limit fungsi f(x) = (√x - 2)/(x - 4) saat x mendekati 4.
Jika kita coba substitusi x = 4, kita mendapatkan bentuk 0/0, sehingga kita perlu mengalikan dengan faktor sekawan.
Kita kalikan pembilang dan penyebut dengan (√x + 2):
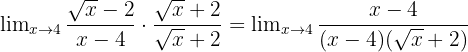
Setelah disederhanakan, kita dapatkan:
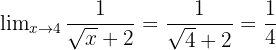
Jadi, nilai limitnya adalah ¼.
Contoh Soal Limit Fungsi Aljabar dan Jawabannya
Sekarang mari kita lihat beberapa contoh soal limit fungsi aljabar kelas 12 agar kamu lebih memahami bagaimana konsep limit diterapkan dalam soal-soal matematika. Berikut adalah beberapa soal dan pembahasan limit fungsi yang dapat kamu pelajari:
Contoh 1:
Tentukan limit dari fungsi f(x) = (x² - 9)/(x - 3) saat x mendekati 3.
Penyelesaian:
Substitusi x = 3, kita mendapat 0/0 (tak tentu).
Faktorkan x² - 9 menjadi (x - 3)(x + 3):
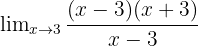
Menghilangkan faktor (x - 3):
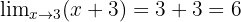
Jadi, nilai limitnya adalah 6.
Contoh 2:
Tentukan limit dari fungsi f(x) = (x³ - 8)/(x - 2) saat x mendekati 2.
Penyelesaian:
Substitusi x = 2, kita mendapat 0/0 (tak tentu).
Faktorkan x³ - 8 menjadi (x - 2)(x² + 2x + 4):
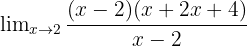
Menghilangkan faktor (x - 2):
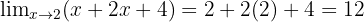
Jadi, nilai limitnya adalah 12.
Contoh 3:
Tentukan limit dari fungsi f(x) = (√x - 1)/(x - 1) saat x mendekati 1.
Penyelesaian:
Substitusi x = 1, kita mendapat 0/0 (tak tentu).
Kalikan pembilang dan penyebut dengan (√x + 1):
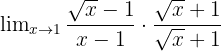
Menyederhanakan:
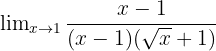
Menghilangkan faktor (x - 1):
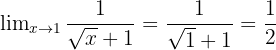
Jadi, nilai limitnya adalah ½.
Begitulah penjelasan lengkap terkait limit fungsi aljabar kelas 12. Jika kesulitan memahami materi limit, jangan ragu untuk bergabung dalam kursus privat Superprof! Kami juga bisa membantu jika kamu kesulitan mengerjakan soal limit mendekati 0 ataupun materi integral. Belajar bersama kami memberikan keuntungan yaitu:
- Penjelasan yang lebih interaktif dan mudah dipahami.
- Latihan soal yang disesuaikan dengan kebutuhan.
- Bisa belajar kapan saja dan di mana saja.
Dengan guru yang berpengalaman dari superprof kamu bisa belajar sesuai dengan kebutuhanmu, misalnya grafik limit. Yuk, tingkatkan pemahaman limit fungsi aljabar dengan belajar di Superprof sekarang juga!
Pahami konsep bilangan rasional dalam tulisan Kami lainnya!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
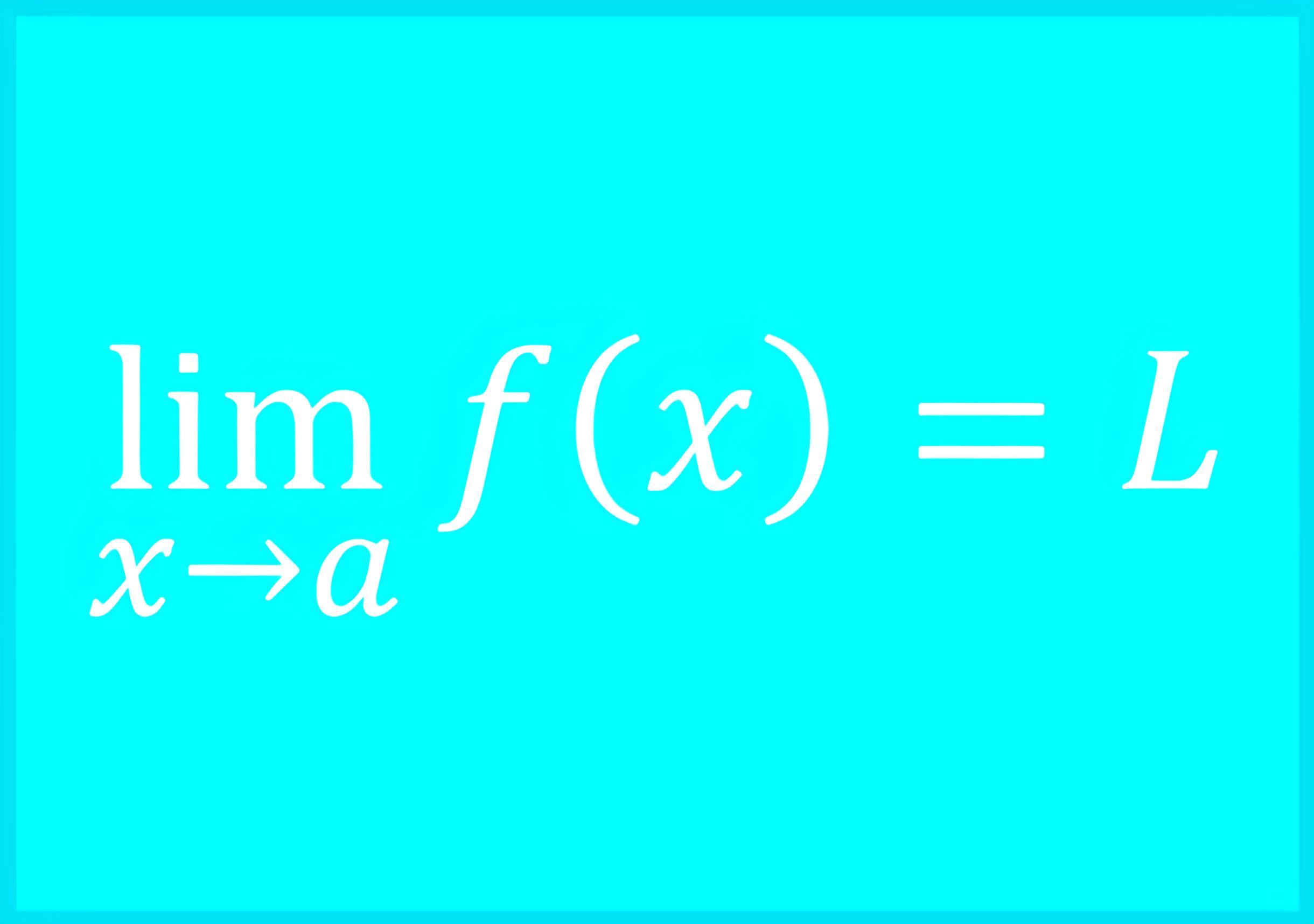
Anu open joki gak min?
enggak kak