Sigma merupakan huruf ke 18 dalam alfabet Yunani yang memiliki berbagai aplikasi penting dalam berbagai bidang keilmuan. Logo sigma digambarkan dengan "∑", sering digunakan dalam operasi matematika. Selain itu sigma dalam fisika juga sangatlah berperan penting. lambang sigma besar ini digunakan untuk membantu menyederhanakan penulisan penjumlahan. Sementara itu, lambang sigma kecil yaitu σ, sangat berperan penting dalam ilmu statistika. Selain itu, dalam program spreadsheet seperti Excel, simbol sigma s juga digunakan sebagai simbol sum untuk menghitung penjumlahan angka dengan cepat. lambang sigma di keyboard hp
Cek disini untuk les privat matematika terbaik
Pengertian Notasi Sigma Dalam Matematika
Notasi sigma, yang merupakan abjad ke 18 huruf Yunani adalah cara singkat untuk menuliskan penjumlahan dari suku-suku dalam suatu deret yang mengikuti pola tertentu. Tidak sembarang angka bisa dijumlahkan menggunakan notasi sigma—suku-suku yang dijumlahkan harus mengikuti aturan dan pola tertentu. Sebagai contoh, jika kita ingin menjumlahkan angka-angka dari 1 hingga 10, kita bisa menulisnya dalam bentuk notasi Sigma seperti berikut:
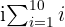
Dengan ∑, kita cukup menyebutkan bahwa kita ingin menjumlahkan angka dari 1 sampai 10, tanpa perlu menulis angka-angka tersebut satu per satu. Sangat praktis, bukan?
Periksa di sini jika ingin mengetahui pengertian dari bilangan berpangkat
Notasi sigma logo ∑ pertama kali diperkenalkan oleh matematikawan asal Swiss bernama Leonhard Euler, pada tahun 1755. Euler memilih simbol ∑ karena mengacu pada istilah SUM (jumlah) dalam bahasa Inggris yang diwakili oleh huruf pertama dari kata tersebut, yaitu "S", yang disimbolkan dengan ∑ dalam bahasa Yunani. Sigma sum ini tentu sangat berkaitan erat dengan deret dan barisan artimatika dan geometri.
Apakah uraian diatas semudah Anda memahami penjelasan Kami tentang pengertian eksponen?
Rumus Notasi Sigma
Menghafal rumus dalam matematika menjadi modal utama Anda saat Anda ingin menyelesaikan berbagai soal matematika. Tak terkecuali soal notasi sigma. Meskipu n rumus notasi sigma terlihat mudah namun seringkali banyak dari Anda yang terkecoh. Itulah mengapa guru Anda di sekolah atau bahkan tutor Anda di rumah meminta Anda menghafal rumus notasi sigma dengan serius.
Temukan sekarang les matematika murah di dekat Anda
rumus notasi sigma:
Σ = notasi sigma;
Ui = suku ke-i;
i = indeks penjumlahan;
p = batas bawah indeks untuk penjumlahan; dan
n = batas atas indeks untuk penjumlahan.
p bisa dimulai dari angka berapapun, ya. Misalnya, i = 1, i = 2, i = -1, dan seterusnya.
Pahami juga tentang KPK dan FPB dalam matematika dasar!
Contoh:
notasi sigma tentu harus mengacu pada bentuk umum yang telah ada, yaitu sebagai berikut.
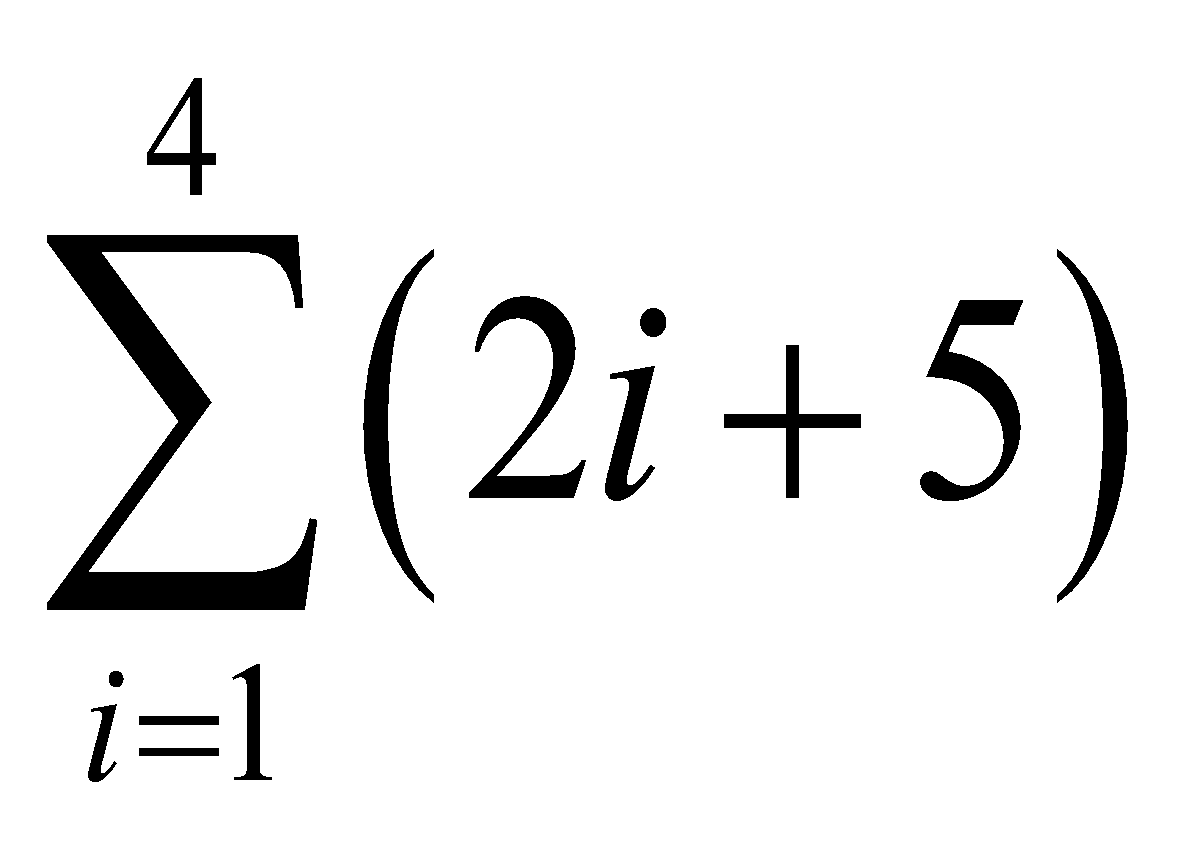
Penyelesaian:
Mengacu pada bentuk umum notasi sigma, diketahui:
Ui = 2i + 5
Artinya, Anda harus menjumlahkan semua suku (2i + 5) untuk i = 1 sampai i = 4. Dengan demikian:
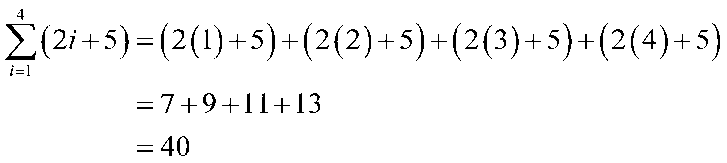
Klik disini untuk mempelajari tentang pola bilangan dalam Matematika!
Sifat-sifat Notasi Sigma
Notasi Sigma memiliki beberapa sifat yang sangat berguna dalam menyelesaikan berbagai permasalahan matematika dan fisika. Berikut adalah beberapa sifat-sifat notasi Sigma yang sering digunakan dan dapat membantu kita mengerjakan soal-soal yang berkaitan dengan penjumlahan.
Sifat 1: Penjumlahan Konstanta
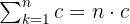
Jika kita menjumlahkan konstanta c dari k = 1 hingga n, hasilnya adalah n dikali c. Artinya, penjumlahan konstanta c sebanyak n kali menghasilkan hasil yang setara dengan perkalian antara n dan c.
Sifat Ini Memiliki Bentuk Yang Lebih Umum, Yaitu:
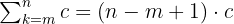
Sifat 2: Penjumlahan dengan Faktor Perkalian
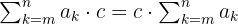
Jika penjumlahan dari a_k dikali dengan konstanta c, maka kita bisa mengeluarkan konstanta c dari penjumlahan. Jadi, penjumlahan a_k yang dikali dengan c setara dengan c dikali penjumlahan dari a_k.
Sifat 3: Penjumlahan dari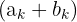 
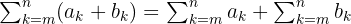
Jika ada dua fungsi a_k dan b_k yang dijumlahkan dalam Sigma, hasil penjumlahannya dapat dipisahkan menjadi penjumlahan dari a_k dan penjumlahan dari b_k secara terpisah. Penjumlahan dua ekspresi dalam Sigma dapat dipecah menjadi dua penjumlahan terpisah.
Sifat 4: Penjumlahan dari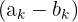 
Sama halnya dengan sifat sebelumnya, tetapi kali ini ekspresi yang dijumlahkan adalah (a_k - b_k). Penjumlahan ini dapat dipisahkan menjadi dua penjumlahan terpisah, yaitu a_k dikurangi b_k.
Sifat 5: Penjumlahan dari 0
Jika semua nilai yang dijumlahkan adalah 0, maka hasil penjumlahan tersebut adalah 0. Artinya, penjumlahan dari angka nol berkali-kali tetap menghasilkan nol.
Sifat 6: Perubahan Indeks Penjumlahan
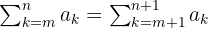
Jika indeks penjumlahan digeser (misalnya dari k=m menjadi k=m+1), hasil penjumlahan tetap sama. Ini berarti batas bawah dan batas atas penjumlahan dapat digeser tanpa mengubah hasilnya.
Sifat 7: Perubahan Indeks dengan Perpindahan
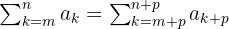
Jika indeks penjumlahan digeser ke depan atau ke belakang, hasil penjumlahan tetap sama selama fungsi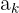 
tetap konsisten. Ini berarti kita dapat menggeser indeks dan mengubah ekspresi sesuai dengan perubahan tersebut tanpa mengubah hasil akhir.
Sifat 8: Menjumlahkan Dua Indeks yang Berbeda
Menunjukkan bahwa kita bisa mengganti indeks k dengan indeks j, selama batas bawah dan atas penjumlahan serta fungsi yang terlibat tetap sama. Artinya, variabel indeks dalam penjumlahan tidak mempengaruhi hasil akhir jika batasnya sama.
Notasi Sigma logo ∑ adalah simbol yang sangat berguna dalam matematika, fisika, bahkan kehidupan sehari-hari, bahkan lambang sigma di keyboard hp pun bisa ditulis saat ini. Selain itu, sifat-sifat yang ada dalam Sigma memungkinkan kita untuk memanipulasi penjumlahan dengan cara yang lebih fleksibel. Dengan memahami dasar-dasar Sigma, kita dapat lebih mudah menangani berbagai masalah yang melibatkan penjumlahan banyak suku.
Jika Anda sedang kesusahan memahami notasi Sigma dan penerapannya dalam matematika, jangan ragu untuk mencari les matematika di Superprof. Di sini, Anda bisa belajar langsung dengan tutor yang berpengalaman. Siapa tahu, pembelajaran ini bisa membuka jalan bagi Anda untuk menguasai konsep-konsep matematika yang lainnya!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
