Anda mungkin telah mengenal notasi ilmiah, atau pernah mendengar istilah tersebut. Ciri dari notasi ilmiah adanya bilangan berpangkat untuk meringkas penulisan angka yang terlalu besar atau bahkan terlalu kecil misal saat menuliskan masa dari elektron yaitu 9,1 x 10-31 kg. Bilangan berpangkat yang ada dalam contoh tersebut tentunya Anda pelajari dalam matematika. Seperti yang telah Anda ketahui, bahwa Matematika ada di semua lini ilmu pengetahuan Alam. Contoh lainnya adalah ketika seorang ahli antariksa menentukan jarak Bumi ke Mataari yang berjarak milyaran kilometer, tentunya mereka akan menggunakan bilangan berpangkat untuk mempermudah dalam penulisannya.
Bilangan berpangkat tersebut dikenal dengan nama bilangan eksponen. Bilangan eksponen digunakan agar bilangan dapat lebih mudah ditulis dan menjadi lebih singkat atau lebih sederhana sehingga akan memudahkan untuk dipahami. Anda mungkin masih kebingungan saat mengetahui bahwa bilangan berpangkat disebut juga dengan eksponen, padahal dalam pikiran Anda bilangan berpangkat hanya sebatas pada 22 dan 32 yang Anda pelajari semasa di SD. Namun ada baiknya bagi Anda untuk terus membaca tulisan ini agar lebih memahami apa itu bilangan eksponen.
Temukan sekarang les privat matematika terbaik!

Pengertian Eksponen
Secara sederhana eksponen adalah perkalian berulang atau perkalian bilangan sama yang diulang terus menerus. Dalam memahami bilangan eksponen Anda tidak cukup hanya hafal perkalian saja, tetapi Anda juga perlu memahami sifat-sifat dan bentuk lain dari eksponen.
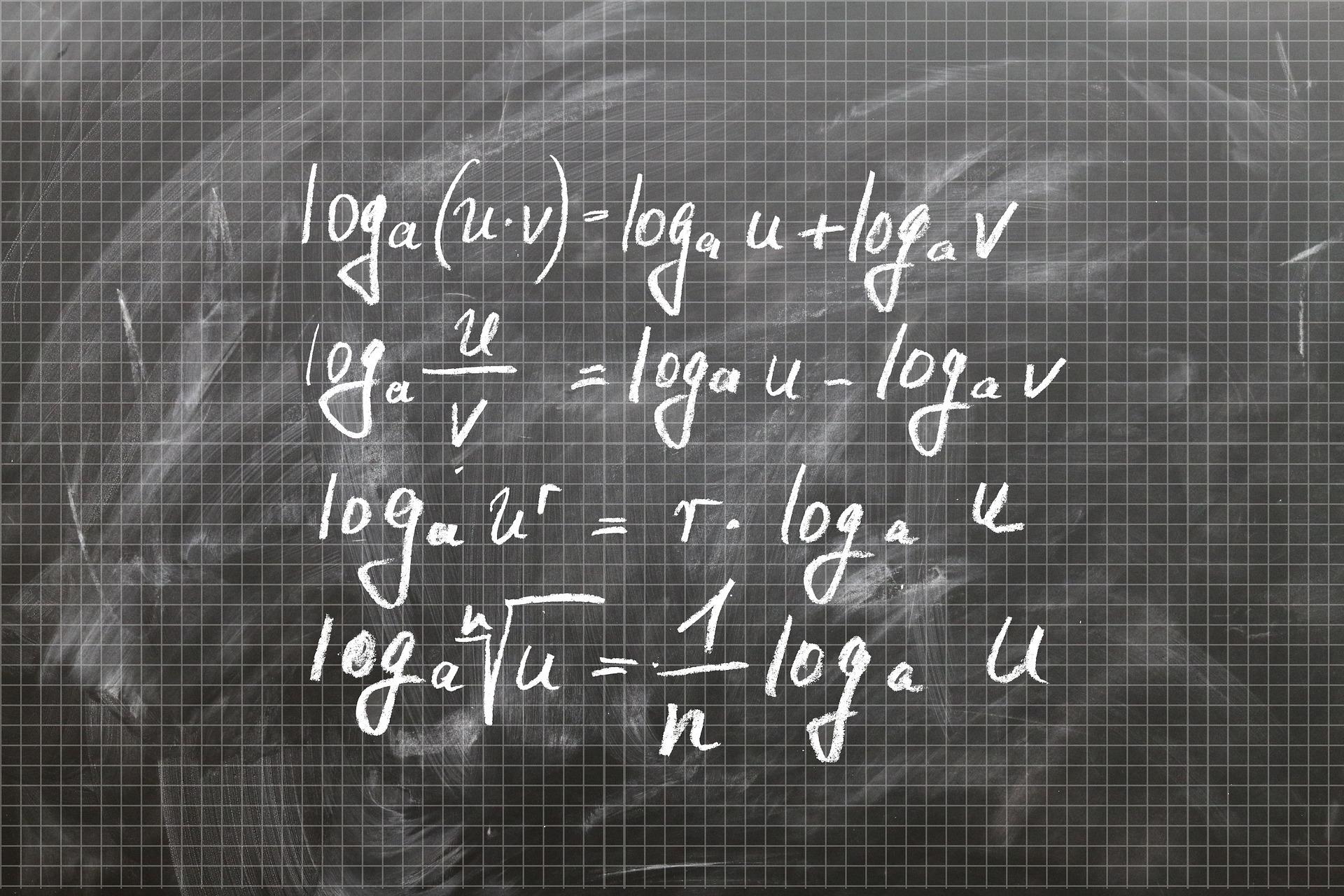
Konsep eksponen sendiri telah ditemukan sejak zaman Yunani kuno sekitar tahun 335 SM oleh seorang ahli Matematika yang bernama Euclid atau Euclides yang dikenal dengan nama Bapak Geometri. Namun penggunakan bilangan eksponen pada era modern yang tercatat dalam sejarah dilakukan oleh Michael Stifel yang merupakan seorang ahli matemarika. Michael Stifel menuliskan konsep bilangan eksponen pada bukunya yang berjudul “Arithmetica Integra” yang diterbitkan pada tahun 1544.
Setelahnya penggunaan eksponen telah banyak digunakan dalam berbagai bidang, tidak hanya matematika namun seluruh bidang Ilmu Pengetahun Alam seperti Fisika, Kimia, dan Astronomi.
Bentuk umum eksponen adalah:

a adalah bilagan real dan b adalah bilangan asli
Dari bentuk di atas, a disebut sebagai basis atau bilangan pokok, sedangkan b disebut sebagai pangkat atau eksponen. Jika b termasuk bilangan bulat positif, maka ab bisa dinyatakan seperti berikut.
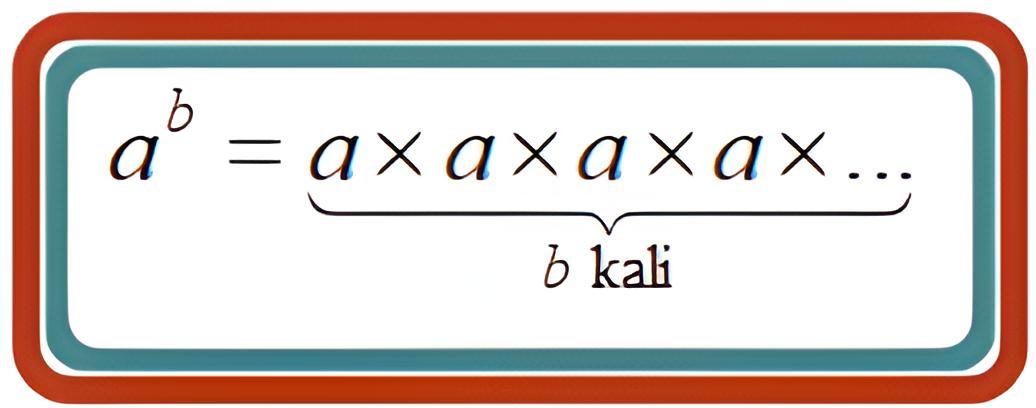
Jika sudah paham pengertian eksponen, kalian perlu baca juga pengertian sigma dalam matematika!
Sifat Sifat Eksponen
Saat Anda ingin benar benar memahami bilangan eksponen, Anda juga harus memahami sifat dari bilangan eksponen. Sifat dalam bilangan eksponen memiliki peranan penting dalam bilangan berpangkat. Sifat eksponen antara lain:
- Pangkat Penjumlahan
Pangkat penjumlahan hanya berlaku jika Anda mengalikan dua eksponen atau lebih dengan basis yang sama. Jika basis berbeda maka sifat eksponen ini tidak berlaku. Contoh
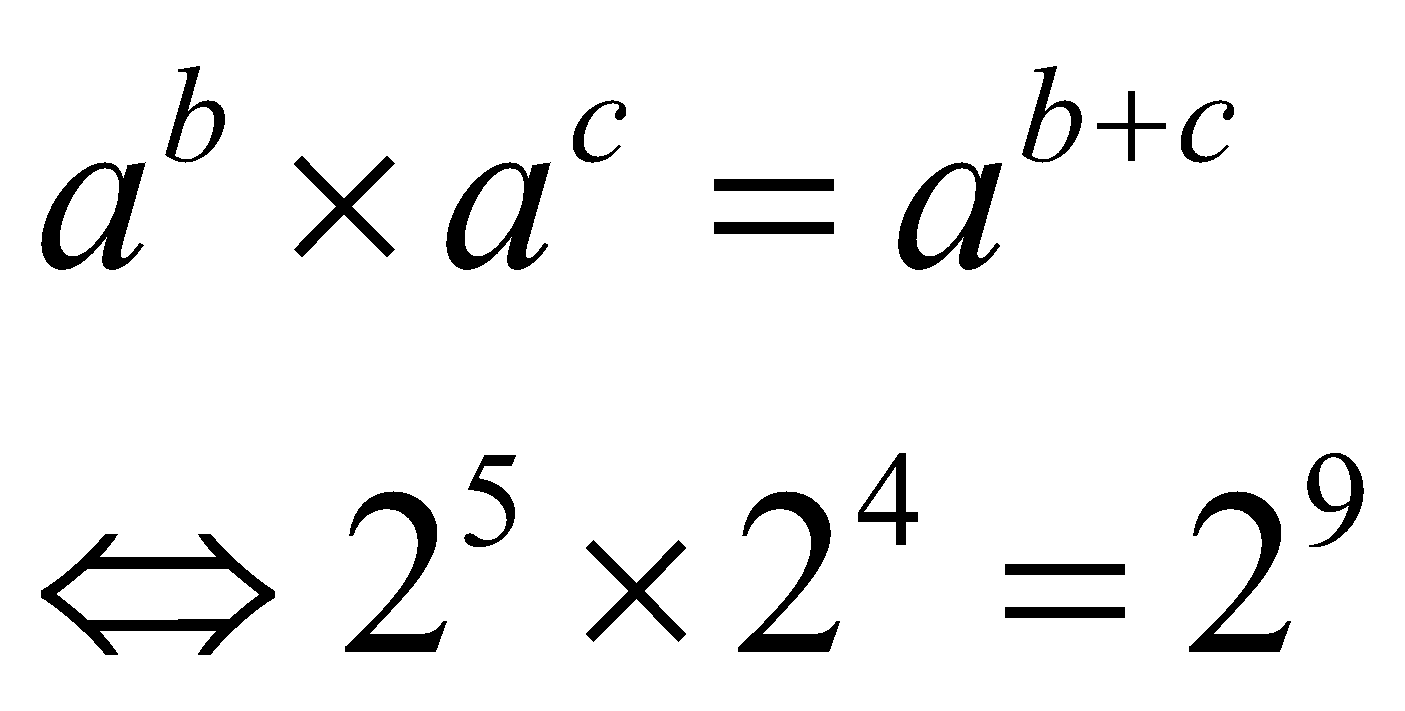
- Pangkat Pengurangan
Pangkat pengurangan hanya berlaku jika Anda melakukan pembagian antara dua eksponen atau lebih dengan basis yang sama. Sifat ini juga hanya berlaku untuk basis yang sama. Contoh
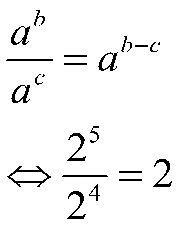
Klik disini untuk mempelajari pola bilangan dalam matematika!
- Pangkat Perkalian
Sifat pangkat perkalian akan berlaku jika suatu eksponen dipangkatkan lagi. Contoh:
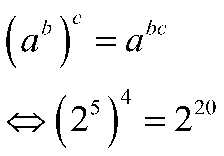
- Pangkat Pembagian.
Sifat pangkat pembagian berlaku jika suatu ekponen berada di dalam bentuk akar atau bisa disebut dengan akar eksponen. Jika Anda tidak bisa mengingat penulisan akar eksponen lihatlah contoh berikut:
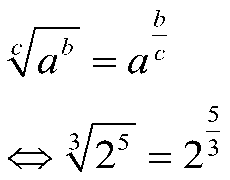
Ketahui juga perbedaan KPK dan FPB dalam matematika!
- Pangkat Nol
Jika Anda melihat ada sebuah bilangan yang dipangkatkan no, maka Anda bisa menuliskannya sebagai 1. Semua bilangan yang dipangkatkan 0 sama dengan 1. Syarat dari bilangan ini a tidak boleh 0. Contoh:
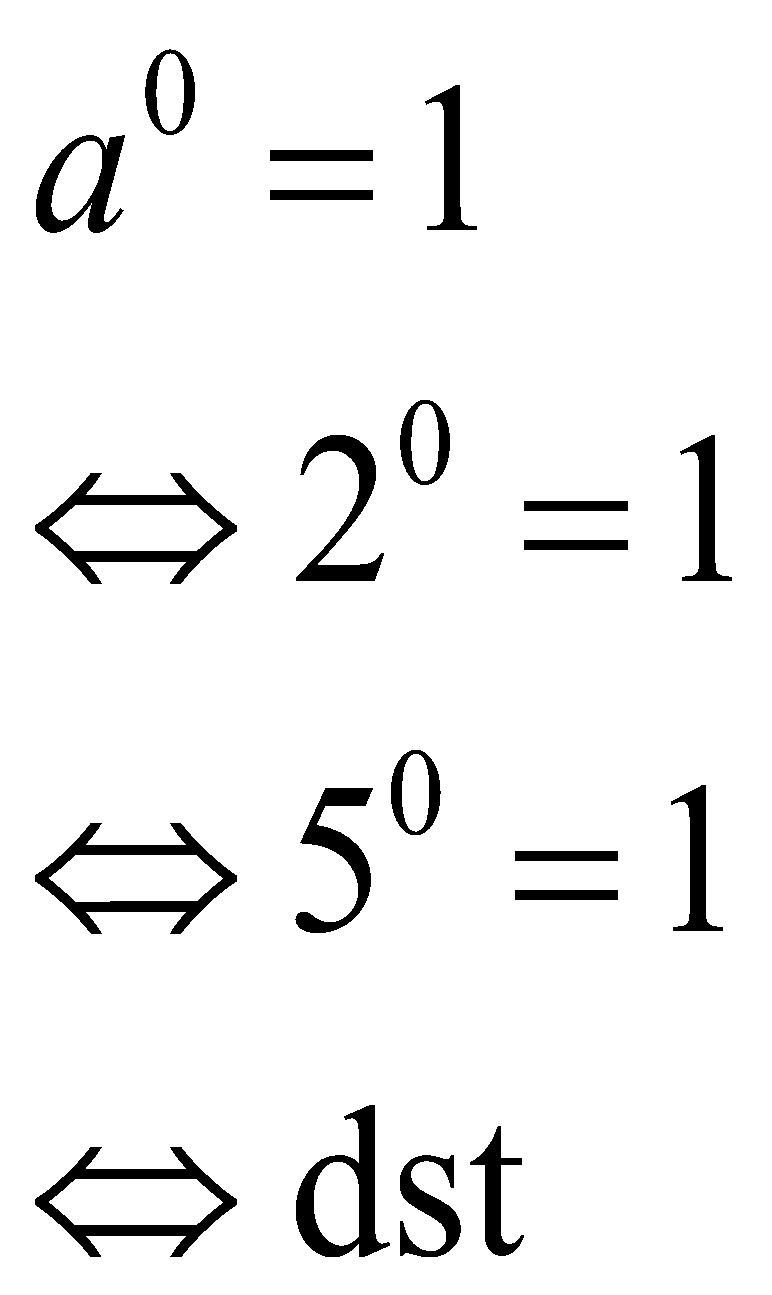
- Pangkat Satu
Anda perlu lebih jeli dan teliti saat memahami tentang sifat eksponen pangkat 1, karena beberapa orang merasa kebingungan saat membedakan pangkat nol dan pagkat 1. Suatu bilangan jika dipangkatkan satu maka hasilnya sama dengan bilangan itu sendiri. Contoh:
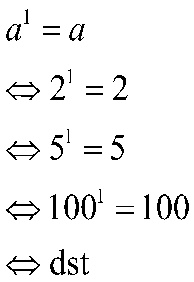
- Perkalian Bilangan yang dipangkatkan
Pada sifat eksponen ini berlaku jika terdapat dua bilangan di dalam kurung, kemudian diberi pangkat, maka kedua bilangan tersebut akan memiliki pangkat yang sama. Contoh:
(a x b)c = ac x ac
(3 x 5)2 = 32 x 52
- Pangkat bilangan pecahan
Pada sifat eksponen ini baik bilangan pembilan dan penyebutnya harus dipangkat semua. Dengan syarat bilangan pembilang tidak boleh 0. Contoh:
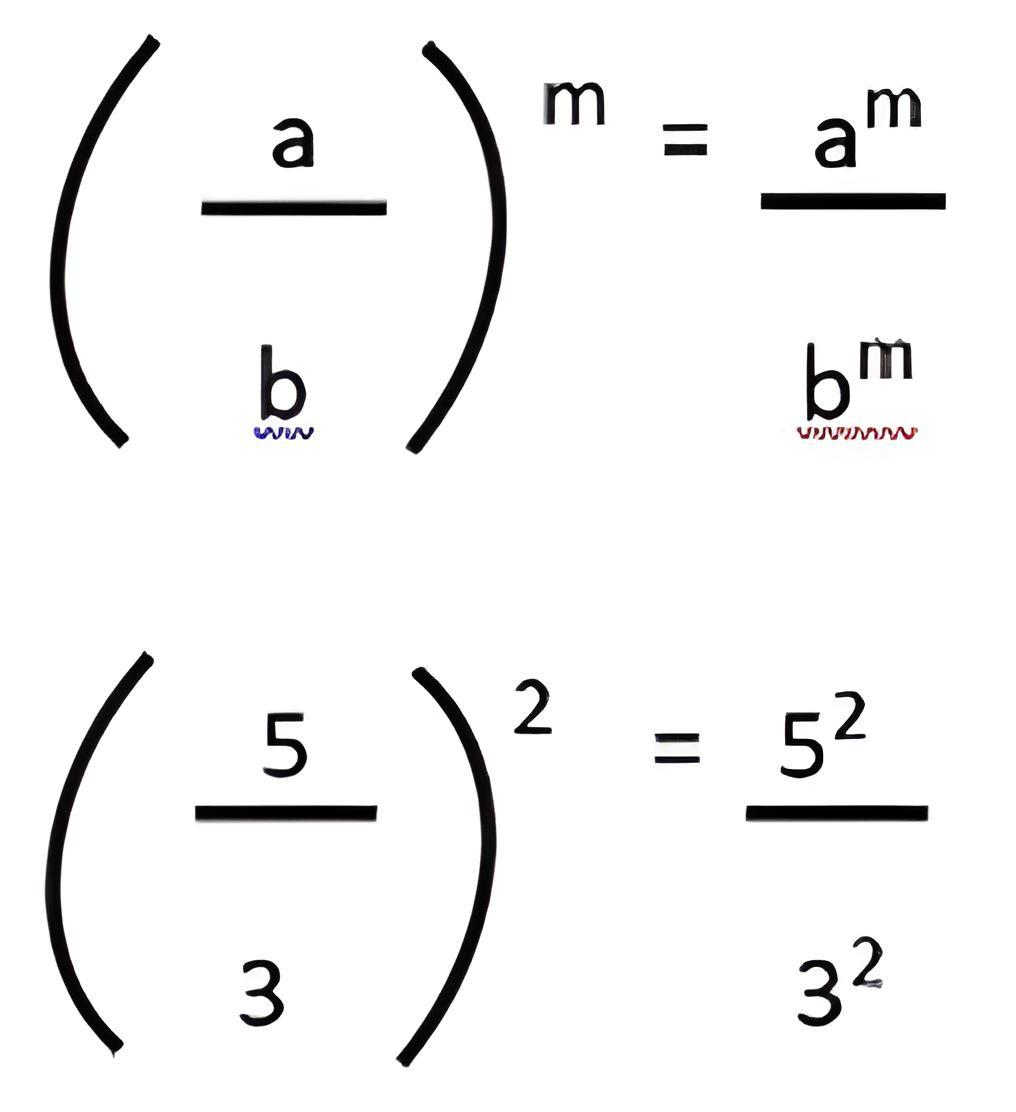
- Pangkat Negatif
Pada sifat eksponen ini perpangkatan negatif akan menghasilikan suatu pecahan. Sifat pangkat negatif artinya satu per perkalian berulang suatu bilangan dengan dirinya sendiri. Contoh:
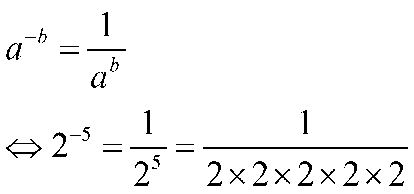
Dalam memahami bilangan eksponen Anda harus memahami konsep dasar dari eksponen itu sendiri. konsep dasar ini disebut juga dengan sifat eksponen. Jika Anda benar benar telah memahami sifat dari eksponen maka Anda akan dengan mudah menggunakan eksponen untuk menyelesaikan pekerjaan dan menjawab berbagai persoalan matematika yang berhubungan dengan eksponen.
Tentunya tidak semua orang akan mudah memahami bilangan eksponen meskipun banyak diantara Anda telah membaca dan bahkan menelaah tentang sifat-sifat eksponen. Beberapa dari Anda merasa bahwa Matematika bukanlah kawan baik Anda. Bahkan perkalian dasar mungkin sering Anda lupakan. Tetapi kita tidak bisa sepenuhnya menghilangka Matematika dalam kehidupan Anda, terutama jika Anda masih seorang pelajar. Matematika adalah pelajaran wajib yang bahkan akan Anda temui hingga jenjang pendidikan tinggi. Anda tidak bisa menghindarinya.
Namun terdapat berbagai cara untuk mengatasi kesulitan Anda. Anda dapat belajar Matematika bersama dengan teman Anda yang memang menyukai Matematika dan pintar dalam hal tersebut. Anda bisa meminta bantuan teman untuk menjelaskan tentang bilang eksponen. Jika Anda terlalu malu dan engga untuk bertanya tidak ada yang salah jika Anda memilih belajar bersama tutor. Tutor adalah pilihan terbaik saat ini jika kita berbicara tentang belajar diluar jam sekolah.
Tutor matematika sangat beragam, mulai dari seorang guru matematika di sekolah, hingga mahasiswa yang menjadi tutor diluar jam perkuliah mereka. Banyak dari mereka yang memberikan pelajaran tambahan untuk anak SD hingga SMA. Superprof adalah platfrom yang menyediakan tutor berkualitas. Anda bisa belajar melalui pembelajaran online yang menggunakan penggilan video, atau bahkan Anda bisa belajar langsung dengan tatap muka. Anda juga bisa mendiskusikan biaya kursus dengan calon tutor Anda, dan Anda tidak perlu membayarnya jika Anda tidak merasa cocok. Superprof juga memberikan percobaan pertama gratis jika Anda ingin mencoba mana tutor yang sesuai dengan kriteria Anda. Apapun pilihan Anda, Superprof akan memberikan solusinya.
Bukalah situs kami dan lakukan pencarian cepat untuk tutor yang berkualitas.
Ringkaskan dengan AI