Bilangan berpangkat adalah salah satu konsep dasar dalam matematika yang sangat berguna dalam berbagai bidang, mulai dari perhitungan sehari-hari hingga aplikasi ilmiah yang lebih kompleks. Dalam artikel ini, kita akan membahas pengertian, rumus, dan sifat-sifat bilangan berpangkat kelas 8 yang sering muncul dalam perhitungan matematika. Memahami konsep ini akan mempermudah kita dalam menyelesaikan berbagai masalah matematika dan aplikasinya di berbagai disiplin ilmu. Mari kita mulai dengan pemahaman dasar terlebih dahulu!
Cek disini untuk les privat matematika
Pengertian Bilangan Berpangkat
Bilangan berpangkat adalah hasil dari perkalian berulang suatu bilangan yang disebut basis, yang dipangkatkan oleh suatu bilangan lain yang disebut bilangan eksponen. Dengan kata lain, bilangan berpangkat memungkinkan kita untuk menulis perkalian yang panjang menjadi bentuk yang lebih ringkas. Sebagai contoh, alih-alih menulis 3 kali 3 kali 3, kita cukup menulisnya dengan bentuk eksponen yaitu 
. Mudah, kan?
Secara umum, rumus pangkat dapat ditulis dengan bentuk 
, di mana:
- a adalah basis atau bilangan pokok yang akan dikalikan.
- n adalah eksponen atau pangkat yang menyatakan berapa kali basis tersebut dikalikan.
Sebagai contoh,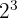 
berarti 
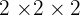= 8. Jadi, 2 dipangkatkan 3 menghasilkan 8.
Jika sudah paham pengertian bilangan berpangkat, pahami juga pengertian sigma dalam Matematika!
Sifat-Sifat Bilangan Berpangkat
Setelah memahami apa pengertian bilangan berpangkat kelas 9, kini saatnya kita menggali lebih dalam tentang sifat sifat eksponensial. Sifat-sifat ini adalah aturan dasar yang memungkinkan kita untuk menyederhanakan bilangan berpangkat agar lebih mudah mengerjakannya. Berikut ini adalah sifat eksponensial yang perlu kamu pahami agar lebih mudah mengerjakan bilangan berpangkat:
1. Penjumlahan Bilangan Berpangkat
Sifat Pangkat Penjumlahan berlaku ketika kamu mengalikan dua bilangan berpangkat yang memiliki basis yang sama. Menurut sifat ini, kita cukup menjumlahkan pangkatnya dan tetap mempertahankan basis yang sama.
Rumus:
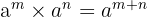
Jadi, jika kamu mengalikan dua bilangan berpangkat yang memiliki basis yang sama, kamu dapat langsung menjumlahkan pangkatnya. Misalnya, dalam contoh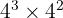 
, kita dapat menjumlahkan pangkatnya menjadi 
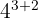= 4 pangkat 5.
2. Pangkat Pengurangan
Kebalikan dari sifat sebelumnya, Sifat Pangkat Pengurangan berlaku ketika kamu membagi dua bilangan berpangkat yang memiliki basis sama. Menurut sifat ini, kita dapat mengurangkan pangkatnya dan tetap mempertahankan basis yang sama.
Rumus:
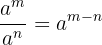
Jadi, ketika kamu membagi dua bilangan berpangkat dengan basis yang sama, kamu cukup mengurangi pangkatnya saja. Sebagai contoh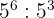 
, kita dapat mengurangi pangkatnya menjadi 
.
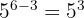3. Pangkat Perkalian
Sifat Pangkat Perkalian berlaku ketika ada bilangan perpangkatan yang dipangkatkan lagi. Dalam hal ini, kamu harus mengalikan pangkatnya.
Rumus:
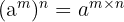
Jika ada suatu bilangan yang dipangkatkan dengan bilangan berpangkat lainnya, kamu cukup mengalikan pangkatnya. Kita lihat contoh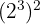 
, kamu dapat mengalikan pangkatnya menjadi 
.
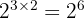4. Perkalian Pangkat
Sifat Perkalian Bilangan yang Dipangkatkan berlaku ketika kamu mengalikan dua bilangan yang dipangkatkan. Dalam hal ini, masing-masing bilangan dipangkatkan terlebih dahulu, kemudian hasilnya pangkatkan.
Rumus:
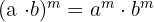
Jika ada perkalian antara dua bilangan yang dipangkatkan, kamu cukup memisahkan pangkatnya dan menghitung pangkat masing-masing bilangan. Misalnya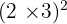 
, kamu dapat memisahkannya menjadi 
.
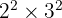5. Perpangkatan pada Bilangan Pecahan
Sifat Perpangkatan pada Bilangan Pecahan berlaku ketika ada bilangan pecahan yang dipangkatkan. Dalam hal ini, pembilang dan penyebut bilangan pecahan harus dipangkatkan secara terpisah.
Rumus:
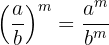
Jadi jika ada bilangan pecahan yang dipangkatkan, kamu dapat memisahkan pangkatannya ke pembilang dan penyebutnya. Contohnya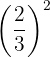 
, kamu dapat menghitungnya menjadi 
.
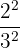6. Pangkat Negatif
Sifat Pangkat Negatif menyatakan bahwa bilangan berpangkat negatif dapat diubah menjadi bentuk pecahan dengan pembilang 1 dan penyebut bilangan berpangkat positif.
Rumus:
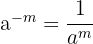
Jika ada bilangan berpangkat negatif, kamu dapat langsungmengubahnya menjadi pecahan dengan membalik bilangan dan mengubah pangkatnya menjadi positif. Misalnya, dalam contoh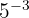 
, kamu dapat menghitungnya sebagai 
.
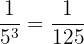Temukan les matematika murah di lokasi Anda
7. Pangkat Pecahan
Sifat Pangkat Pecahan menyatakan bahwa jika ada akar pada bilangan berpangkat, pangkat akar dapat dituliskan sebagai pecahan dengan penyebutnya.
Rumus:
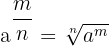
Jika bilangan berpangkat berbentuk pecahan, maka pangkat penyebut adalah akar dari angka tersebut. Sebagai contoh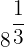 
, kamu dapat menghitungnya menjadi 
.
8. Pangkat Nol
Sifat Pangkat Nol menyatakan bahwa setiap bilangan yang dipangkatkan dengan nol akan menghasilkan 1, kecuali jika basisnya adalah 0.
Rumus:
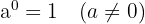
Jadi, setiap bilangan yang dipangkatkan dengan nol akan selalu menghasilkan 1, selama bilangan basisnya bukan 0. Misalnya, 
, 
.
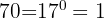Bilangan Negatif Berpangkat
Selain sifat-sifat eksponen pangkat bulat positif di atas, kita juga perlu memahami sifat bilangan berpangkat jika basisnya bernilai negatif. Tergantung pada apakah pangkatnya ganjil atau genap, hasil dari bilangan berpangkat akan berbeda.
- Jika Berpangkat Ganjil
Jika bilangan negatif dipangkatkan dengan pangkat ganjil, hasilnya akan tetap negatif.
Contoh:
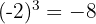
- Jika Berpangkat Genap
Jika bilangan negatif dipangkatkan dengan pangkat genap, hasilnya akan positif.
Contoh:
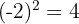
Klik disini untuk melihat contoh soal untuk materi lainnya!
Contoh Soal Eksponen Kelas 10
Setelah memahami pengertian dan sifat-sifat bilangan berpangkat, kini saatnya untuk melatih pemahamanmu tersebut dengan beberapa contoh soal eksponen kelas 10. Soal-soal berikut akan membantumu untuk lebih memahami bagaimana cara menerapkan sifat-sifat eksponen. Berikut adalah beberapa contoh soal eksponen kelas 10 yang dapat membantu kamu memperdalam pemahaman mengenai materi ini:
Soal eksponen kelas 9 1: Hitung hasil dari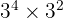 
.
Pembahasan:
Berdasarkan sifat pangkat penjumlahan, maka kita dapat menjumlahkan pangkatnya karena basisnya sama. Maka, kita punya:
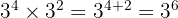
Selanjutnya, kita hitung:
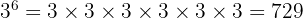
Jadi, hasil dari 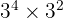adalah 729.
Contoh soal eksponen kelas 10 2: Hitung hasil dari .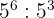
Pembahasan:
Dengan menggunakan sifat pangkat pengurangan, kita dapat mengurangi pangkatnya karena basisnya sama. Maka, dapat disimpulkan:
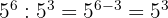
Selanjutnya, kita hitung:
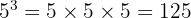
Jadi, hasil dari 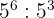adalah 125.
Soal bilangan berpangkat kelas 9 3: Hitung hasil dari .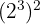
Pembahasan:
Menggunakan sifat pangkat perkalian, kita kalikan pangkatnya. Maka, kita punya:
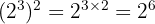
Selanjutnya, kita hitung:
Jadi, hasil dari 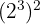adalah 64.
Soal eksponen kelas 9 4: Hitung hasil dari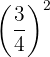 
.
Pembahasan:
Menggunakan sifat perpangkatan pada bilangan pecahan, kita pangkatkan pembilang dan penyebutnya. Maka, kita punya:
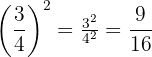
Jadi, hasil dari 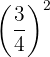adalah 
.
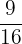Soal eksponen kelas 9 5: Hitung hasil dari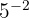 
.
Pembahasan:
Dengan menggunakan sifat pangkat negatif, kita tahu bahwa pangkat negatif sama dengan inversi dari pangkat positif. Maka, kita punya:
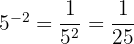
Jadi, hasil dari 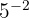adalah 
.
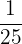Contoh soal eksponen kelas 10 6: Hitung hasil dari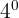 
.
Pembahasan:
Menurut sifat pangkat nol, setiap bilangan yang dipangkatkan dengan 0 akan menghasilkan 1 (selama basisnya bukan 0). Maka, dapat disimpulkan:
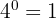
Jadi, hasil dari 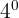adalah 1.
Soal bilangan berpangkat kelas 9 7: Hitung hasil dari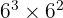 
.
Pembahasan:
Dengan menggunakan sifat pangkat penjumlahan, kita dapat menambahkan pangkatnya karena basisnya sama. Maka, kita punya:
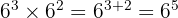
Selanjutnya, kita hitung:
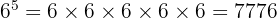
Jadi, hasil dari 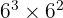adalah 7776.
Soal eksponen kelas 9 8: Hitung hasil dari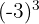 
.
Pembahasan:
Karena pangkatnya ganjil, hasil dari bilangan negatif akan tetap negatif. Maka, dari itu dapat ditulis:
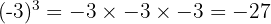
Jadi, hasil dari 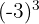adalah -27.
Contoh soal eksponen kelas 10 9: Hitung hasil dari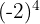 
.
Pembahasan:
Karena pangkatnya genap, hasil dari bilangan negatif akan menjadi positif. Maka, dapat disimpulkan:
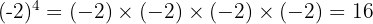
Jadi, hasil dari 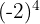adalah 16.
Soal eksponen kelas 9 10: Hitung hasil dari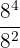 
.
Pembahasan:
Dengan menggunakan sifat pangkat pengurangan, kita dapat mengurangi pangkatnya karena basisnya sama. Maka, kita punya:
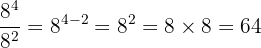
Jadi, hasil dari 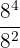adalah 64.
Latihan Soal
Berikut adalah 5 latihan soal bilangan berpangkat kelas 9 mengenai bilangan berpangkat agar kamu semakin paham:
- Hitung
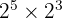. - Hitung
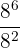. - Hitung
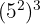. - Hitung
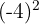. - Hitung
.
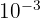Secara keseluruhan, bilangan berpangkat adalah konsep dasar yang sangat penting dalam matematika, terutama ketika kamu melangkah ke materi yang lebih kompleks seperti akar kuadrat dan logaritma. Dengan memahami rumus dan sifat-sifat bilangan berpangkat, kamu akan lebih mudah menyelesaikan soal-soal matematika yang berkaitan dengan eksponen. Ingat, semakin sering kamu berlatih, semakin mahir kamu dalam menerapkan materi pangkat matematika ini. Jadi, jangan ragu untuk terus belajar dan menggali lebih dalam. Jika merasa perlu bantuan lebih, bergabunglah dengan Superprof untuk mendapatkan bimbingan yang sesuai dengan gaya belajarmu.
Ikuti artikel Kami lainnya untuk menambah khazanah keilmuan kalian tentang KPK dan FPB pada Matematika dasar!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
