“Matematika adalah ilmu yang paling murah. Tidak seperti fisika atau kimia, matematika tidak memerlukan peralatan mahal. Yang dibutuhkan untuk matematika hanyalah pensil dan kertas.” - George Polya
Persamaan kuadrat merupakan salah satu topik penting dalam matematika yang seringkali menjadi bahan pembelajaran di berbagai tingkat pendidikan. Untuk memahami lebih dalam tentang persamaan kuadrat, kita perlu mengenal rumus-rumus yang terkait dengannya, seperti rumus abc, pemfaktoran, dan konsep kuadrat sempurna. Artikel ini akan membahas secara mendalam tentang persamaan kuadrat serta penerapan rumus-rumus tersebut.
Cek di sini untuk les matematika di Medan


Pengertian Persamaan Kuadrat
Persamaan kuadrat adalah persamaan polinomial yang memiliki pangkat tertinggi dua. Secara umum, bentuk persamaan kuadrat dapat dituliskan sebagai ax²+bx+c=0, di mana a, b, dan c adalah koefisien bilangan real dan a tidak boleh sama dengan nol. Dalam persamaan tersebut, x merupakan variabel, ax² merupakan suku kuadrat, bx merupakan suku linear, dan c merupakan konstanta.
Cek di sini untuk les olimpiade matematika Jakarta
Bagaimana Cara Menyelesaikan Persamaan Kuadrat?
Nah, ada tiga cara utama yang digunakan untuk menyelesaikan persamaan kuadrat kelas 9: pemfaktoran, rumus ABC, dan melengkapi kuadrat sempurna. Yuk, kita bahas satu per satu!
1. Pemfaktoran
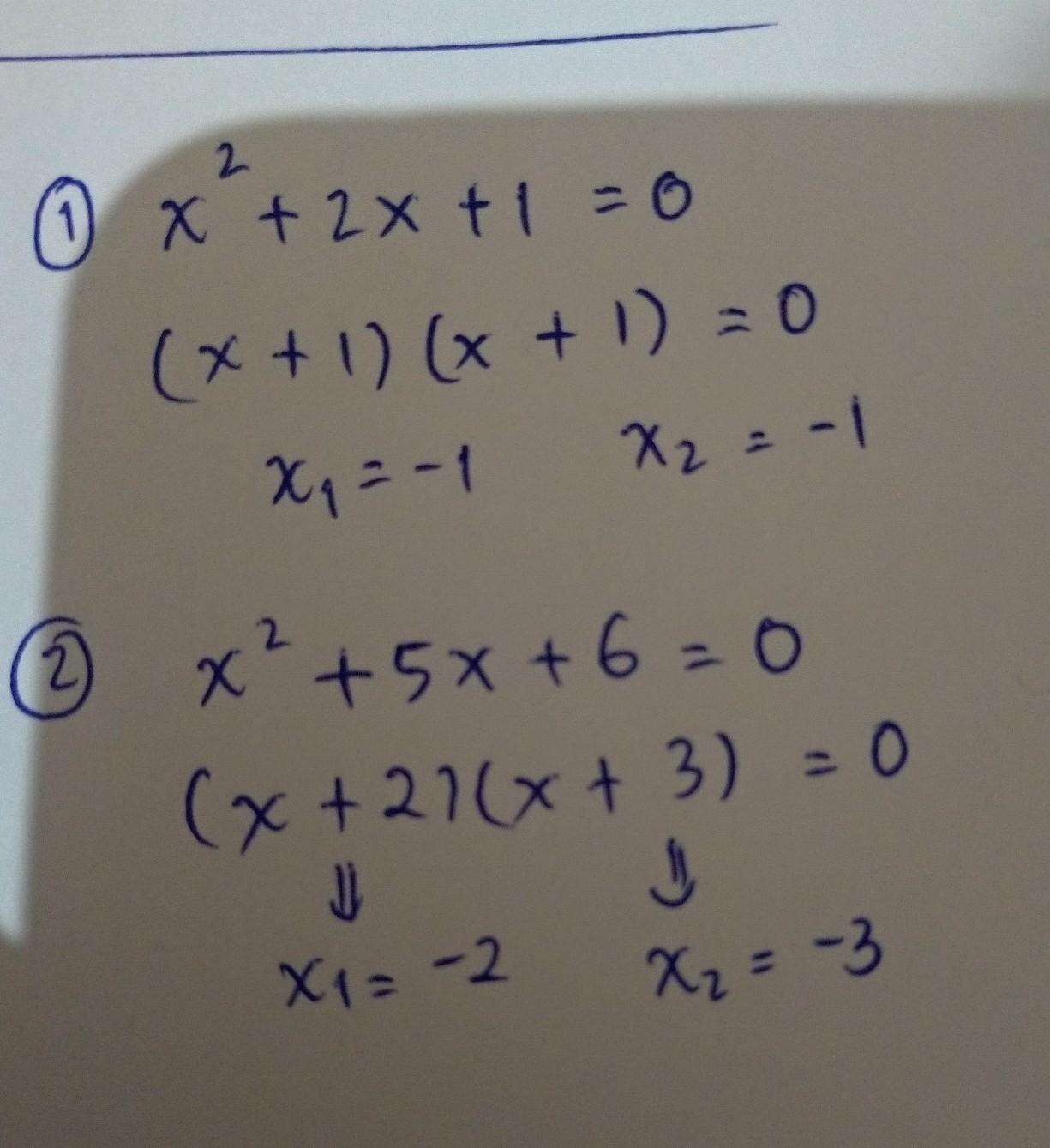
Pemfaktoran adalah salah satu cara klasik untuk menyelesaikan rumus persamaan kuadrat. Jika persamaan kuadrat yang diberikan bisa difaktorkan, metode ini adalah pilihan yang sangat efisien. Rumus pemfaktoran melibatkan pencarian dua angka yang jumlahnya sama dengan koefisien b dan hasil kalinya sama dengan hasil perkalian antara a dan c.
Secara sederhana, jika kita punya persamaan kuadrat dalam bentuk ax^2 + bx + c = 0, kita harus mencari dua bilangan yang ketika dijumlahkan menghasilkan b, dan ketika dikalikan menghasilkan a * c.
Cara Menggunakan Pemfaktoran
- Tentukan dua angka yang jumlahnya b dan hasil kalinya a * c.
- Ubah persamaan kuadrat menjadi bentuk dua binomial yang dikalikan.
- Tentukan akar-akar persamaan dari faktorisasi tersebut.
Contoh Soal Pemfaktoran
Mari kita lihat contoh soal pemfaktoran berikut:
Soal: Selesaikan persamaan kuadrat x^2 + 7x + 10 = 0.
Penyelesaian:
- Kita mencari dua angka yang jika dijumlahkan menghasilkan 7 dan jika dikalikan menghasilkan 10. Angka tersebut adalah 5 dan 2.
- Jadi, persamaan x^2 + 7x + 10 = 0 bisa difaktorkan menjadi (x + 5)(x + 2) = 0.
- Dari sini, kita dapat menemukan akar persamaan dengan menyamakan masing-masing faktor dengan nol:
x + 5 = 0 atau x + 2 = 0,
sehingga x = -5 atau x = -2.
Jadi, solusi dari persamaan kuadrat ini adalah x = -5 dan x = -2.
Lihat artikel kami tentang algoritma.
2. Rumus ABC
Jika persamaan kuadrat tidak dapat difaktorkan, rumus ABC persamaan kuadrat adalah solusi yang bisa diandalkan. Rumus kuadratik ini adalah cara cepat dan pasti untuk menemukan akar-akar persamaan kuadrat. Rumus akar persamaan kuadrat ABC adalah:
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
Di sini, ±\pm menunjukkan bahwa kita bisa mendapatkan dua nilai akar—yang satu dengan tanda plus dan yang lainnya dengan tanda minus. Ingat ya, bagian dalam akar disebut sebagai diskriminan (b^2 - 4ac), yang berfungsi untuk menentukan jenis solusi yang kita dapatkan.
- Jika diskriminan lebih besar dari 0 (b^2 - 4ac > 0), kita akan mendapatkan dua akar berbeda.
- Jika diskriminan sama dengan 0 (b^2 - 4ac = 0), kita hanya akan mendapatkan satu akar tunggal.
- Jika diskriminan kurang dari 0 (b^2 - 4ac < 0), maka persamaan tersebut tidak memiliki akar real.
Cara Menggunakan Rumus ABC
- Tentukan nilai a, b, dan c dari persamaan kuadrat yang diberikan.
- Hitung diskriminan (b^2 - 4ac).
- Gunakan rumus ABC untuk mencari akar persamaan kuadrat.
Contoh Soal Menggunakan Rumus ABC
Soal: Selesaikan persamaan kuadrat 2x^2 - 4x - 6 = 0.
Penyelesaian:
- Identifikasi nilai a, b, dan c:
a = 2, −4b = -4, dan c = -6. - Hitung diskriminan:
b^2 - 4ac = (-4)^2 - 4(2)(-6) = 16 + 48 = 64. - Karena diskriminan lebih besar dari 0, kita akan mendapatkan dua solusi. Sekarang, masukkan nilai b dan diskriminan ke dalam rumus ABC: x = \frac{-(-4) \pm \sqrt{64}}{2(2)} = \frac{4 \pm 8}{4}
- Dengan tanda plus:
x = \frac{4 + 8}{4} = \frac{12}{4} = 3.
Dengan tanda minus:
x = \frac{4 - 8}{4} = \frac{-4}{4} = -1.
Jadi, akar-akar persamaan kuadrat ini adalah x = 3 dan x = -1.

Lihat artikel kami tentang konjektur.
3. Melengkapi Kuadrat Sempurna
Metode melengkapi kuadrat sempurna adalah cara untuk menyelesaikan persamaan kuadrat dengan mengubahnya menjadi bentuk kuadrat sempurna. Kuadrat sempurna adalah bilangan yang dapat ditulis sebagai hasil perkalian suatu bilangan dengan dirinya sendiri, seperti (x + d)^2.
Misalnya, jika kita memiliki persamaan x^2 + 6x = 7, kita bisa melengkapi kuadrat sempurna untuk menyelesaikannya. Menggunakan rumus kuadrat sempurna, kita dapat mengubah persamaan menjadi bentuk (x + d)^2 = e, yang lebih mudah untuk diselesaikan.
Cara Menggunakan Melengkapi Kuadrat Sempurna
- Pastikan koefisien x^2 adalah 1. Jika tidak, bagi seluruh persamaan dengan koefisien tersebut.
- Pindahkan konstanta ke sisi kanan persamaan.
- Tambahkan bilangan kuadrat sempuran di ruas kiri dan kanan persamaan.
- Selesaikan persamaan yang telah menjadi kuadrat sempurna.
Contoh Soal Melengkapi Kuadrat Sempurna
Soal: Selesaikan persamaan kuadrat x^2 + 6x - 7 = 0.
Penyelesaian:
- Pindahkan -7 ke kanan:
x^2 + 6x = 7. - Tambahkan bilangan kuadrat sempurna yaitu (6/2)^2 = 9 di ruas kiri dan kanan persamaan:
x^2 + 6x + 9 = 7 + 9. - Ubah menjadi kuadrat sempurna:
(x + 3)^2 = 16. - Ambil akar kedua sisi persamaan:
x + 3 = \pm 4,
sehingga x = 1 atau x = -7.
Jadi, akar-akar persamaan kuadrat ini adalah x=1x = 1 dan x=−7x = -7.
Pelajari lebih lanjut tentang matematika
Superprof, Tempat Mencari Guru Untuk Belajar Matematika Secara Privat

Jika Anda ingin memperdalam pemahaman Anda tentang persamaan kuadrat atau konsep matematika lainnya, belajar dengan guru privat bisa menjadi solusi yang tepat. Memahami berbagai metode penyelesaian persamaan kuadrat seperti pemfaktoran, penggunaan kuadrat sempurna, dan penerapan rumus abc membutuhkan bimbingan yang tepat dan terarah. Seorang guru privat dapat memberikan perhatian khusus pada kebutuhan belajar Anda, menjelaskan konsep-konsep yang sulit dengan cara yang mudah dimengerti, dan membantu Anda mengatasi tantangan yang Anda hadapi dalam belajar matematika.
Dengan belajar secara privat, Anda bisa mendapatkan penjelasan yang lebih mendalam dan latihan soal yang sesuai dengan tingkat pemahaman Anda. Ini tentu saja akan membantu Anda untuk lebih cepat menguasai materi dan mencapai hasil belajar yang lebih optimal. Tidak hanya itu, seorang guru privat juga bisa memberikan tips dan strategi khusus untuk menyelesaikan soal-soal matematika dengan lebih efektif.
Untuk menemukan guru matematika terbaik yang sesuai dengan kebutuhan dan preferensi Anda, kunjungi website Superprof sekarang juga! Superprof menyediakan berbagai pilihan guru privat dengan latar belakang pendidikan dan pengalaman mengajar yang beragam. Anda dapat membaca profil guru, melihat ulasan dari siswa sebelumnya, dan memilih guru yang paling cocok untuk Anda. Dengan Superprof, Anda bisa belajar kapan saja dan di mana saja, baik secara online maupun tatap muka, sesuai dengan kenyamanan Anda.
Jangan lewatkan kesempatan untuk meningkatkan kemampuan matematika Anda dengan bimbingan dari guru-guru terbaik. Mulailah perjalanan belajar Anda bersama Superprof dan rasakan perbedaannya! Kunjungi Superprof hari ini dan temukan guru privat yang dapat membantu Anda mencapai kesuksesan dalam belajar matematika!
Pelajari cara menghitung interval.
Pelajari cara menghitung median
Cari tahu cara memperluas tanda kurung dalam aljabar.
Carilah kursus matematika terbaik di Superprof Indonesia.
Cari tahu cara membuat kerucut menggunakan geometri
Pelajari tentang ubin dan pengubinan.
Pelajari cara menghitung hasil bagi.
Ringkaskan dengan AI















Harus benar
Semoga
Cara memfaktorkan
Persamaan kuadrat matematika
Gak ngerti matematika..tapi lulus kelas mipa
memang faktor keberuntungan itu diperlukan di berbagai aspek kehidupan