Sebelum masuk lebih jauh, mari kita mulai dari hal paling dasar. Sebenarnya, apa sih logaritma itu? Banyak siswa yang langsung merasa pusing begitu mendengar kata “logaritma”, padahal konsep dasarnya cukup sederhana. Logaritma adalah kebalikan dari pemangkatan atau eksponen. Kalau pada eksponen kita mencari hasil pangkatnya, maka pada logaritma kita justru mencari besar pangkatnya. Inilah alasan mengapa logaritma sering disebut sebagai operasi invers dari perpangkatan.
Jadi, intinya begini. Jika kita sudah tahu hasil pemangkatan suatu bilangan, logaritma membantu kita mencari pangkat berapa yang menghasilkan nilai tersebut. Memang, untuk contoh sederhana seperti 2 pangkat berapa yang hasilnya 8, jawabannya mudah ditemukan. Namun, tidak semua soal sesederhana itu, apalagi jika bilangan yang terlibat berupa desimal seperti 5 pangkat berapa yang hasilnya 2,236. Di sinilah logaritma berperan penting karena membantu menemukan jawaban secara sistematis tanpa harus menebak-nebak nilai pangkat, sehingga materi ini menjadi sangat penting dalam logaritma kelas 10.
Pengertian Logaritma
Sekarang kita bahas pengertian logaritma dengan lebih pelan. Secara sederhana, pengertian logaritma adalah operasi matematika untuk mencari besar pangkat suatu bilangan pokok. Bilangan pokok ini biasa disebut sebagai basis.
Dengan kata lain, logaritma menjawab pertanyaan “dipangkatkan berapa?”. Jadi, ketika kita melihat bentuk logaritma, sebenarnya kita sedang diminta menentukan nilai pangkat tertentu.
Contohnya seperti ini. Jika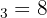 
, maka bentuk logaritmanya adalah 
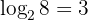. Artinya, bilangan 2 harus dipangkatkan 3 agar hasilnya 8.
Dalam materi logaritma kelas 10, contoh-contoh seperti ini sangat sering digunakan. Tujuannya agar siswa benar-benar memahami hubungan antara perpangkatan dan logaritma.
Kalau hubungan ini sudah dipahami, maka belajar sifat-sifat logaritma dan rumus logaritma akan terasa jauh lebih mudah.
Manfaat Logaritma
Sekarang mungkin muncul pertanyaan lain. “Sebenarnya, buat apa sih belajar logaritma?” Pertanyaan ini wajar, terkadang gak masuk logika, apalagi kalau masih merasa logaritma itu rumit.
Logaritma sangat bermanfaat untuk menyelesaikan persoalan yang melibatkan pangkat, terutama jika bilangannya besar atau berbentuk desimal. Dengan logaritma, perhitungan menjadi lebih ringkas dan terstruktur.
Dalam dunia pendidikan, materi logaritma membantu melatih cara berpikir logis dan analitis. Tidak heran jika logaritma selalu muncul dalam pelajaran matematika tingkat menengah hingga lanjut. Kalau kamu ingin memperdalam materi ini secara fleksibel, kamu juga bisa belajar lewat kursus matematika online.
Dalam kehidupan sehari-hari, fungsi logaritma juga sering digunakan. Misalnya dalam perhitungan pH pada kimia, intensitas bunyi dalam fisika, hingga skala gempa bumi.
Jadi, meskipun terlihat abstrak, logaritma matematika sebenarnya sangat dekat dengan kehidupan nyata.
Bentuk Umum Logaritma
Setelah memahami pengertian logaritma, sekarang kita bahas bentuk dan rumus logaritma. Tenang saja, tidak perlu takut duluan.
Bentuk umum logaritma biasanya dituliskan sebagai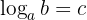 
. Artinya, bilangan a dipangkatkan c akan menghasilkan b.
Di sini, a disebut basis atau bilangan pokok. Sedangkan b disebut numerus, yaitu bilangan hasil pemangkatan.
Dalam materi logaritma kelas 10, siswa sering keliru membedakan basis dan numerus. Padahal, kuncinya sederhana. Basis itu “angka kecil” di bawah log, sedangkan numerus adalah angka yang ditulis setelah log.
Kalau sudah paham bagian ini, memahami rumus logaritma akan terasa jauh lebih mudah.
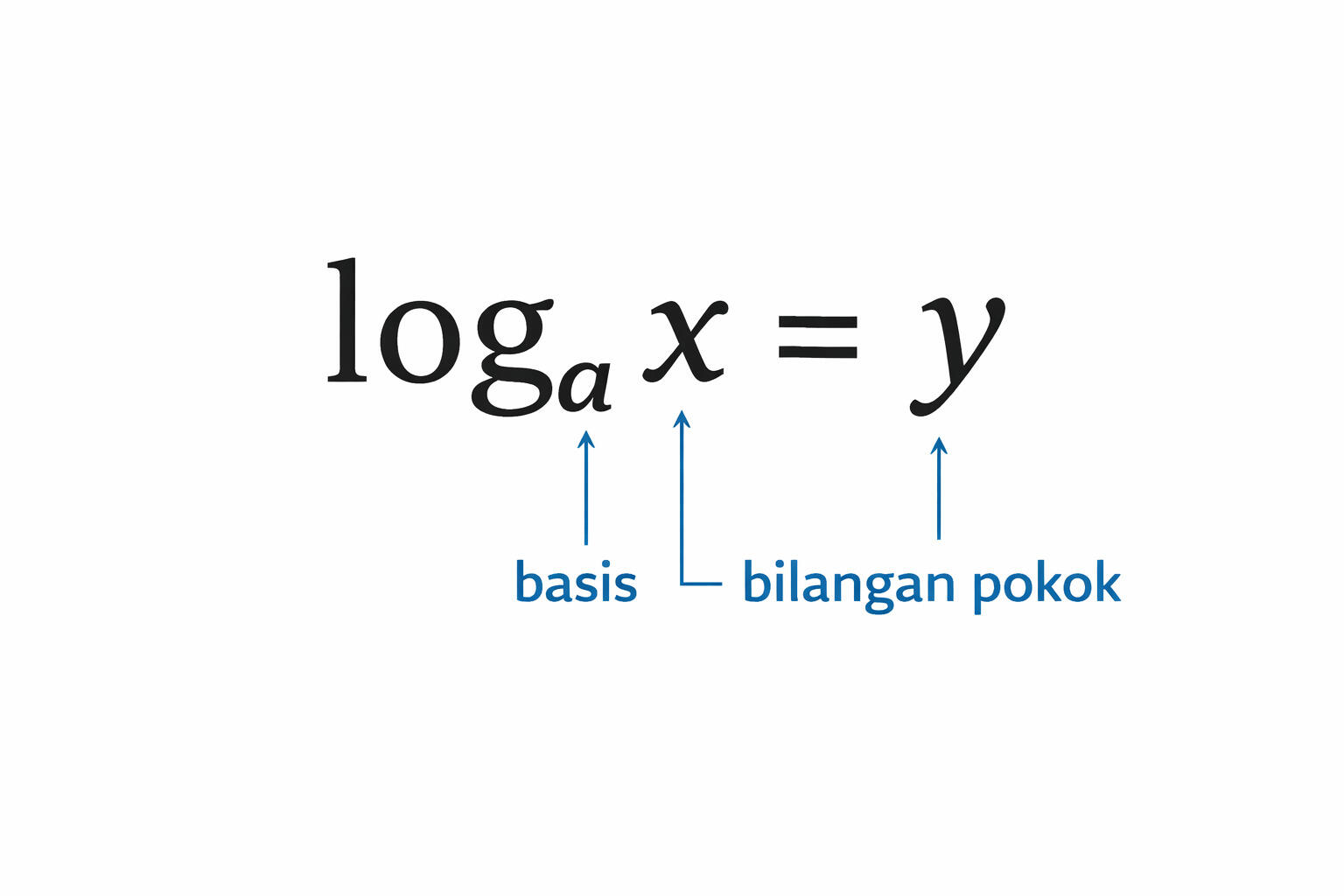
Untuk memperdalam pemahaman, mari kita amati beberapa ilustrasi berikut terlebih dahulu. Contoh-contoh ini menunjukkan hubungan antara bentuk perpangkatan dan bentuk logaritma sehingga konsepnya menjadi lebih jelas.
Dari contoh-contoh tersebut, pemahaman tentang logaritma biasanya mulai terbentuk. Namun, tidak jarang masih muncul kebingungan dalam menentukan bilangan yang berperan sebagai basis dan bilangan yang menjadi numerus.
Sebagai pedoman sederhana, ingatlah bahwa bilangan pokok atau basis merupakan angka yang terletak sebagai dasar logaritma, sedangkan numerus adalah bilangan hasil perpangkatan yang berada setelah simbol logaritma. Dengan memahami aturan ini, penulisan dan pembacaan logaritma akan menjadi jauh lebih mudah.
Sifat-Sifat Logaritma
Nah, sekarang kita masuk ke bagian penting, yaitu sifat-sifat logaritma. Bagian ini sering muncul dalam soal, jadi wajib dipahami.
Salah satu sifat logaritma yang paling sering digunakan adalah sifat penjumlahan. Sifat ini menyatakan bahwa logₐ (x × y) sama dengan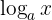 
ditambah 
.
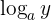Selain itu, ada juga sifat pengurangan logaritma. Jika kita membagi dua bilangan dengan basis yang sama, maka logaritmanya dapat dikurangkan.
Ada pula sifat perpangkatan, yaitu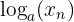 
sama dengan n dikali 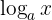. Sifat ini sangat membantu saat menghadapi soal logaritma yang bentuknya panjang.
Dengan memahami sifat sifat logaritma ini, mengerjakan soal akan terasa jauh lebih cepat dan tidak ribet.
Penerapan Logaritma dalam Kehidupan Sehari-hari
Walaupun sering dianggap hanya ada di buku pelajaran, konsep logaritma sebenarnya banyak digunakan dalam kehidupan luas sehari-hari.
Dalam dunia perbankan, logaritma digunakan untuk menghitung waktu yang dibutuhkan agar suatu investasi berkembang dengan bunga tertentu. Perhitungan ini melibatkan fungsi logaritma.
Dalam ilmu kebumian, skala logaritmik digunakan untuk membandingkan kekuatan gempa bumi. Perbedaan kecil pada skala logaritmik bisa berarti perbedaan energi yang sangat besar.
Di bidang sains lainnya, logaritma juga digunakan untuk menganalisis pertumbuhan populasi, intensitas cahaya, dan berbagai data ilmiah lainnya.
Contoh Penerapan:
- Dalam perbankan, logaritma membantu menghitung jangka waktu investasi atau pinjaman dengan tingkat bunga tertentu.
- Pada studi kependudukan, logaritma digunakan untuk menganalisis laju pertumbuhan penduduk dari waktu ke waktu.
- Dalam ilmu kebumian, skala logaritmik digunakan untuk membandingkan energi gempa yang berbeda secara signifikan.
Contoh Logaritma Soal
Agar semakin paham, mari kita lihat beberapa contoh soal logaritma.
Soal 1
Tentukan nilai dari:
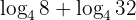
Pembahasan:
Karena basisnya sama, kita bisa langsung menggunakan sifat logaritma penjumlahan. Kedua bilangan tersebut dikalikan terlebih dahulu.
Karena basisnya sama, kita dapat menggunakan sifat logaritma penjumlahan, yaitu:
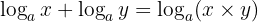
Sehingga diperoleh:
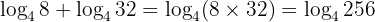
Hasilnya menjadi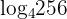 
. Nah, sekarang tinggal mencari 4 pangkat berapa yang hasilnya 256. Jawabannya adalah 4. Jadi, 4 dipangkatkan berapa agar hasilnya 256?
Karena (4^4 = 256), maka:
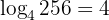
Jawaban:
Hasil dari 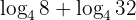adalah 4.
Soal 2
Hitung nilai dari:
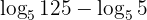
Pembahasan:
Pertama, perhatikan bahwa kedua logaritma memiliki basis yang sama, yaitu 5. Oleh karena itu, kita dapat menggunakan sifat pengurangan logaritma:
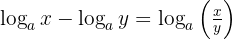
Maka diperoleh:
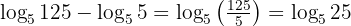
Selanjutnya, tentukan nilai pangkatnya. Jadi, 5 dipangkatkan berapa agar hasilnya 25?
Karena (5^2 = 25), maka:
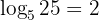
Jawaban:
Nilai dari 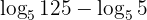adalah 2.
Soal 3
Tentukan nilai dari:
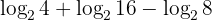
Pembahasan:
Perhatikan bahwa semua logaritma pada soal ini memiliki basis yang sama, yaitu 2. Oleh karena itu, kita dapat menggabungkannya menggunakan sifat penjumlahan dan pengurangan logaritma.
Gabungkan terlebih dahulu:
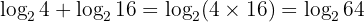
Kemudian kurangkan dengan:
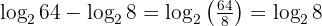
Selanjutnya, tentukan nilai pangkatnya. Jadi, 2 dipangkatkan berapa agar hasilnya 8?
Karena (2^3 = 8), maka:
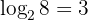
Jawaban:
Hasil dari 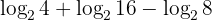adalah 3.
Kesimpulan
Coba kita ringkas lagi tentang kenapa logaritma sepenting itu? Logaritma sendiri adalah konsep dalam matematika yang dipakai mencari besar pangkat bilangan. Kalau kita sudah paham pengertian, rumus, dan sifat-sifat logaritma, materi logaritma kelas 10 ini yang tadinya sulit pelan-pelan jadi lebih mudah dipahami.
“Ah, bukannya mencari pangkat itu gampang?” Misalnya, 2 pangkat berapa yang hasilnya 8, jawabannya jelas 3. Soal-soal semacam ini memang ringan karena bilangannya bulat jadi mudah ditebak. Tapi pernah kepikiran gak sih, kalau soalnya berubah jadi bilangat pangkat. Nah loh, mulai mikir keras, kan?
Logaritma lah yang membantu kita mencari jawaban, tanpa menebak-nebak lagi. Kalau setelah membaca materi logaritma ini kamu masih bingung atau masih kepo dan ingin belajar lebih dalam, termasuk mencari les matematika smp terdekat, belajar bareng tutor Superprof solusinya. Lewat kelas privat matematika di Superprof, kamu akan dibimbing langsung oleh tutor berpengalaman. Buat pengalaman belajarmu jadi gak lagi horoh seperti yang dibayangkan.
Ringkaskan dengan AI
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
