Saat kecil dulu, kita pernah bermain atau setidaknya melihat teman kita bermain kelereng sepulang sekolah. Apakah Anda memperhatikan bahwa jika kelereng diputar begitu cepat, lama-kelamaan akan berhenti bergerak dan diam. Kira-kira, mengapa kelereng itu bisa berhenti berputar? Tepat sekali, seperti kata kunci judul artikel ini, fenomena kelereng ini disebabkan oleh momen inersia.
Apa itu momen inersia? Apa saja yang memengaruhi momen inersia? Bagaimana menghitung momen inersia pada benda? Jangan khawatir, kita akan mengupas materi momen inersia pada artikel ini beserta contoh soal dan pembahasannya. Yuk, simak sampai selesai!

Apa Itu Momen Inersia?
Momen inertia adalah ukuran kecenderungan benda untuk mempertahankan keadaan gerak rotasinya terhadap sumbu putar. Dalam konteks ini, sifat inersia benda dapat diartikan sebagai kemampuan benda tersebut untuk menolak perubahan gerakan rotasinya. Momen inersia berkaitan erat dengan konsep kelembaman, yang merupakan kecenderungan suatu benda untuk tetap diam atau bergerak lurus beraturan. Oleh karena itu, semakin besar momen inersia suatu benda, semakin sulit bagi benda tersebut untuk berubah gerakan rotasinya.
Satuan Momen Inersia
Sementara, satuan momen inersia dalam Sistem Internasional (SI) adalah kilogram meter kuadrat (kg.m²). Ini karena satuan inersia dihitung sebagai hasil kali antara massa benda dan kuadrat jarak benda tersebut terhadap sumbu rotasinya. Misalnya, untuk suatu benda dengan massa 5 kg yang terletak sejauh 2 meter dari sumbu rotasinya, momen inersianya adalah 5 kg x (2 m)² = 20 kg.m². Sementara, simbol momen inersia dalam fisika biasanya dilambangkan dengan huruf kapital "I".
Faktor yang Mempengaruhi Momen Inersia
Faktor yang mempengaruhi momen inersia sangat penting untuk memahami bagaimana benda bereaksi terhadap perubahan gerak rotasinya. Momen inersia adalah ukuran seberapa besar suatu benda dapat menolak perubahan dalam gerak rotasi. Berikut ini adalah penjelasan mendetail mengenai faktor-faktor yang mempengaruhi momen inersia:
1. Massa Benda (m)
Massa adalah faktor utama yang berperan dalam menentukan momen inersia. Semakin besar massa benda, semakin besar pula momen inersia yang dimiliki oleh benda tersebut. Hal ini disebabkan oleh adanya hubungan langsung antara massa benda dan besarnya momen inersia dalam rumus dasarnya,
Misalnya, jika ada dua benda dengan jarak yang sama dari sumbu putar, tetapi satu benda memiliki massa yang lebih besar, maka benda dengan massa yang lebih besar tersebut akan memiliki momen inersia yang lebih besar pula.
2. Jarak dari Sumbu Rotasi (r)
Jarak massa benda dari sumbu rotasi memiliki pengaruh signifikan terhadap momen inersia. Jarak ini dikuadratkan dalam rumus momen inersia, yang berarti bahwa peningkatan jarak akan menyebabkan peningkatan momen inersia yang jauh lebih besar.
- Semakin Jauh Jaraknya: Jika massa suatu benda terletak lebih jauh dari sumbu rotasi, momen inersia akan semakin besar. Sebagai contoh, sebuah pintu yang berputar lebih sulit digerakkan jika kita mendorongnya di dekat engsel dibandingkan dengan mendorongnya di ujung luar.
- Distribusi Massa: Jika massa suatu benda didistribusikan lebih merata dan lebih jauh dari sumbu rotasi, maka momen inersia akan lebih besar. Sebagai contoh, sebuah lingkaran tipis memiliki momen inersia yang lebih besar dibandingkan dengan piringan padat dengan massa dan radius yang sama, karena massa lingkaran tipis terdistribusi lebih jauh dari sumbu rotasinya.
3. Bentuk Geometri Benda
Bentuk geometri benda juga mempengaruhi momen inersia, karena massa benda dapat terdistribusi dalam berbagai pola yang berbeda. Setiap bentuk benda memiliki rumus momen inersia yang berbeda karena distribusi massa yang berbeda pula.
4. Letak Sumbu Rotasi
Letak sumbu rotasi memengaruhi nilai momen inersia secara signifikan. Semakin jauh sumbu rotasi dari pusat massa benda, semakin besar momen inersia yang dimiliki oleh benda tersebut. Beberapa penjelasan terkait hal ini adalah:
- Sumbu di Pusat Massa: Jika sumbu rotasi berada di pusat massa, momen inersia akan lebih kecil dibandingkan jika sumbu tersebut berada di pinggir atau di ujung benda.
- Teorema Sumbu Paralel: Teorema ini menyatakan bahwa momen inersia suatu benda terhadap sumbu baru yang sejajar dengan sumbu asli dapat dihitung dengan menambahkan momen inersia benda terhadap sumbu pusat massa dan hasil kali massa benda dengan kuadrat jarak antara kedua sumbu tersebut.

Rumus Momen Inersia
Momen inersia adalah ukuran seberapa sulit suatu benda untuk diputar terhadap sumbu rotasinya. Rumus momen inersia bervariasi tergantung pada bentuk dan distribusi massa benda, serta letak sumbu rotasinya. Di bawah ini adalah penjelasan mendetail mengenai berbagai rumus momen inersia untuk benda-benda dengan bentuk dan distribusi massa yang berbeda:
Momen Inersia Benda Titik
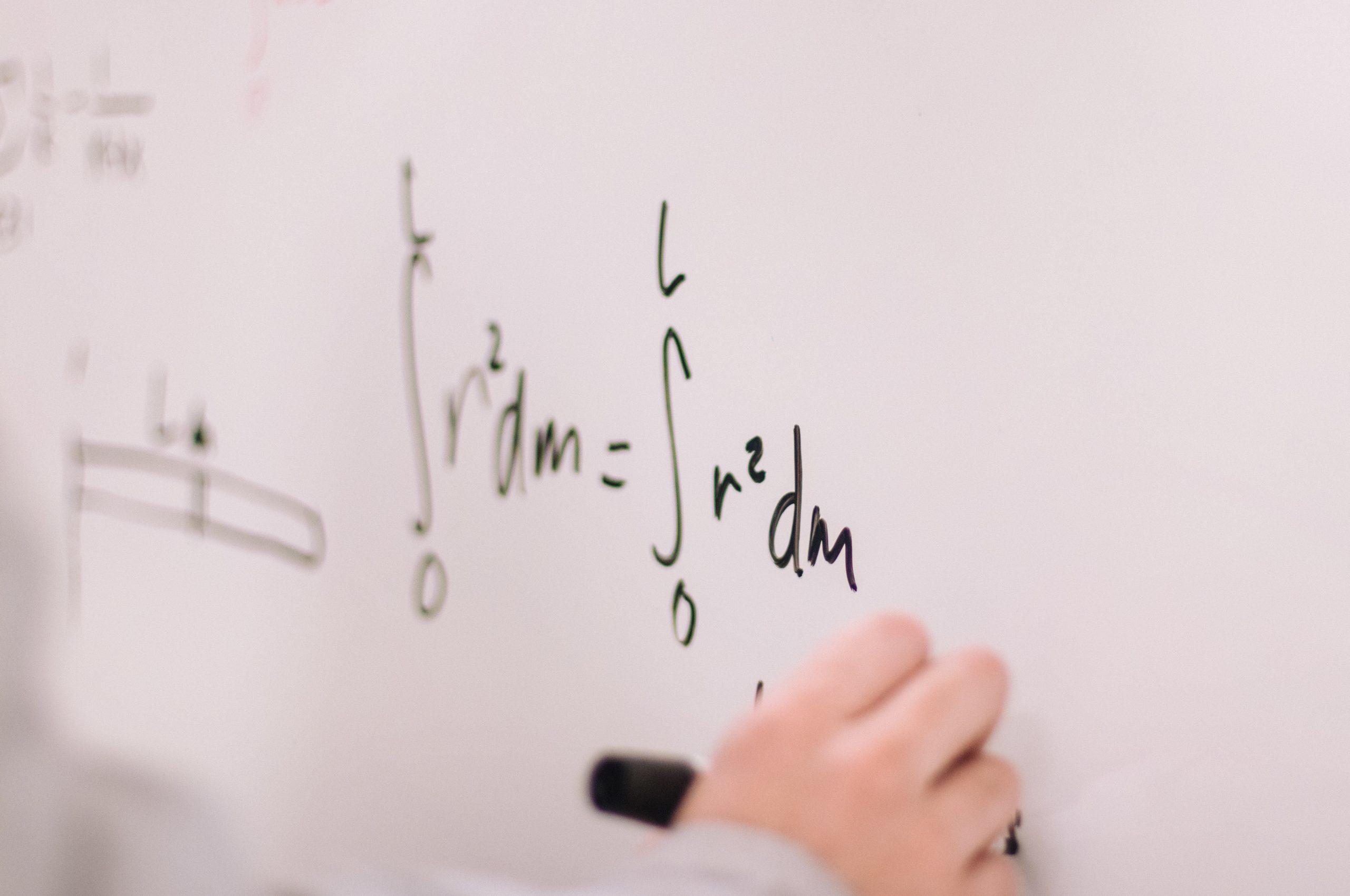
Momen inersia dipengaruhi oleh massa dan jarak terhadap titik putarnya. Rumus momen inersia dapat diartikan sebagai hasil kali massa suatu partikel terhadap kuadrat jarak dari titik poros. Semakin jauh jarak massa benda terhadap poros, semakin besar pula momen inersianya. Secara matematis, rumus momen inersia pada benda titik atau partikel dituliskan sebagai:
I = m.r²
Ketika partikel berjumlah banyak dengan massa (m₁, m₂, m₃, ...) dan jarak (r₁, r₂, r₃) yang berbeda-beda terhadap poros, momen inersianya adalah jumlah total dari momen inersia masing-masing partikel.
∑I = m₁ .r₁² + m₂ .r₂² + m₃ .r₃² + …
I=∫ r².dm
Keterangan:
I = momen inersia (kg.m²)
r = jarak (m)
Momen Inersia Benda Tegar
Selain massa dan jarak, momen inersia juga dipengaruhi oleh bentuk benda seperti bentuk batang silinder, bola pejal cincin, dan sebagainya memiliki nilai momen inersianya masing-masing. Berikut adalah rumus momen inersia pada benda-benda tegar.
| Benda | Poros | Gambar | Momen Inersia |
| Batang | Pusat | 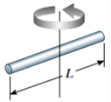 | I = (1/12) m.l² |
| Batang | Ujung | 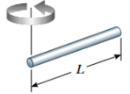 | I = (1/3) m.l² |
| Bola Berongga | Melalui diameter |  | I = (2/3) m.R² |
| Bola Pejal | Melalui diameter |  | I = (2/5) m.R² |
| Silinder Pejal | Sumbu silinder |  | I = (1/2) m.R² |
| Tabung Silinder | Sumbu tabung | 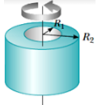 | I = (1/12) m.(R₁²+R₂²) |
| Batang Tipis | Melalui diameter | 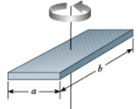 | I = (1/12) m.(a²+b²) |
| Cincin Tipis | Melalui pusat dan tegak lurus jari-jari | 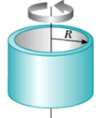 | I = m.R² |
Agar lebih memahami materi momen inersia, mari kita bahas contoh-contoh soal di sub-judul selanjutnya.
Contoh Soal
- Sebuah sistem dibawah ini terdiri dari 3 partikel. Jika m₁ = 2 kg, m₂ = 1 kg dan m₃ = 2 kg, tentukan momen inersia sistem tersebut jika diputar menurut:
a. poros P
b. poros Q
Sumber: saintif.com
Pembahasan:
a. Ip = m₁ .r₁² + m₂ .r₂² + m₃ .r₃²
= 2.0² + 1.1² + 2.2²
= 9 kg m²
b. Iq = m₁ .r₁² + m₂ .r₂² + m₃ .r₃²
= 2.1² + 1.0² + 2.1²
= 4 kg m²
Jadi, momen inersia P adalah 9 kg m² dan momen inersia Q adalah 4 kg m².
- Sebuah bola pejal memiliki massa 4 kg berputar dengan sumbu putar tepat melalui tengahnya. Jika diameter bola tersebut 60 cm hitunglah momen inersia bola tersebut!
Pembahasan:
Diketahui:
m = 4 kg
d = 60 cm
R = 30 cm = 0,3 m
Ditanya:
I ?
Jawab:
Jadi, momen inersianya adalah 0,144 kg m²
I = (2/5) m.R²
I = (2/5).4 .0,3²
I = (2/5).4 .0,09
I = 0,144 kg.m²
- Sebuah batang besi homogen bermassa 4 kg dan panjangnya 0,25 m. Jika sumbu pusatnya terletak pada titik tengah dan tegak lurus batang, momen inersia besi adalah....
Pembahasan:
Diketahui:
m = 4 kg
l = 0,25 m
Ditanya:
I ?
Jawab:
I = (1/12) m.l²
I = (1/12).4 .(0,25)²
I = (1/48) kg.m²
Jadi, momen inersianya adalah 1/48 kg m²
Setelah melihat soal dan pembahasan di atas, apakah Anda semakin paham dengan konsep momen inersia?
Penerapan Momen Inersia dalam Kehidupan Sehari-Hari
Momen inersia merupakan konsep penting dalam fisika yang memiliki banyak penerapan dalam kehidupan sehari-hari. Berikut ini adalah penjelasan mendetail mengenai beberapa penerapan momen inersia:
1. Roda Sepeda
Roda sepeda adalah salah satu contoh paling umum dari penerapan momen inersia. Saat sepeda bergerak, roda berputar pada sumbunya. Momen inersia lingkaran roda sepeda memainkan peran krusial dalam mempertahankan kestabilan sepeda saat melaju.
Semakin besar momen inersia pada roda, semakin stabil sepeda tersebut. Ini karena roda yang memiliki momen inersia besar akan membutuhkan lebih banyak torsi (gaya putar) untuk mengubah kecepatan rotasi atau arah geraknya. Ketika roda berputar, gaya inersia yang dihasilkan menjaga posisi sepeda agar tetap tegak, terutama saat berbelok atau berhadapan dengan guncangan. Dalam hal ini, roda yang lebih besar dan berat (dengan massa lebih) memberikan momen inersia yang lebih besar.
2. Permainan Gasing
Permainan gasing adalah contoh sederhana dari penerapan momen inersia dalam kehidupan sehari-hari. Saat gasing diputar, momen inersia membantu gasing tersebut mempertahankan gerak rotasinya, sehingga bisa tetap berputar stabil selama beberapa waktu.
Gasing berputar dengan cepat, dan momen inersianya membantu mempertahankan kestabilan posisi saat berputar. Semakin besar momen inersia gasing, semakin lama gasing akan bertahan berputar. Ini terjadi karena gaya inersia mencegah perubahan arah atau kecepatan rotasi, sehingga gasing tetap tegak dan tidak terjatuh saat berputar.
3. Mengaduk Minuman
Saat kita mengaduk kopi, teh, atau minuman lainnya di dalam gelas, kita sering melihat bahwa cairan di dalam gelas tetap berputar meskipun kita telah berhenti mengaduk.
Ketika pengaduk digerakkan, energi kinetik ditransfer ke cairan, dan saat pengaduk dihentikan, cairan terus berputar. Ini disebabkan oleh momen inersia cairan yang ingin mempertahankan gerakan rotasinya. Kelembaman cairan menyebabkan air terus berputar karena gaya inersia yang mengakibatkan gerakan berputar tetap berlangsung meski tidak ada lagi gaya luar yang mempengaruhi.

4. Mesin Sentrifugal
Mesin sentrifugal digunakan dalam berbagai aplikasi, baik di laboratorium maupun industri, untuk memisahkan partikel dari larutan. Mesin ini memanfaatkan momen inersia untuk mencapai efisiensi dalam pemisahan.
Mesin sentrifugal beroperasi dengan memutar tabung yang berisi campuran cairan dan partikel. Saat tabung berputar, gaya sentrifugal yang dihasilkan akan mendorong partikel berat ke arah luar, sedangkan cairan yang lebih ringan tetap berada di bagian dalam. Momen inersia dari tabung berputar ini membantu mempertahankan kecepatan rotasinya, yang sangat penting untuk proses pemisahan yang efisien.
5. Flywheel
Flywheel adalah komponen penting dalam banyak mesin, terutama pada mesin kendaraan dan generator. Flywheel berfungsi untuk menyimpan energi rotasi dan menjaga kestabilan operasi mesin.
Flywheel memiliki momen inersia yang besar, yang memungkinkan mereka untuk menyimpan energi kinetik saat berputar. Ketika mesin memerlukan lebih banyak energi, flywheel dapat melepaskan energi yang disimpan, membantu mesin beroperasi lebih halus dan stabil. Dengan momen inersia yang besar, flywheel mengurangi fluktuasi dalam kecepatan putaran mesin.
Momen inersia adalah konsep fundamental dalam fisika yang sangat penting untuk memahami dinamika rotasi benda. Konsep ini membantu kita menganalisis berbagai situasi yang melibatkan gerakan rotasi di sekitar kita. Momen inersia tidak hanya sekadar rumus fisika, ia juga melibatkan pemahaman mendalam tentang bagaimana benda-benda bergerak dan berinteraksi satu sama lain saat berotasi.
Jika Anda merasa tertarik untuk memperdalam pemahaman tentang momen inersia dan fisika secara umum, Superprof siap membantu Anda! Kami memiliki guru berpengalaman yang ahli dalam fisika dan siap membimbing Anda.
Temukan les fisika terbaik di Superprof sekarang juga!
Superprof juga akan membantu Anda memahami konsep perpindahan kalor dan hukum archimedes dengan penjelasan yang mudah dipahami. Sampai jumpa di kelas fisika Superprof kawan!
Ringkaskan dengan AI
















