Pada kesempatan kali ini, kita akan membahas mengenai pembagian polinomial horner. Dengan memahami pembagian horner, kamu dapat menyederhanakan perhitungan polinominal yang mungkin terasa rumit jika menggunakan teknik pembagian konvensional. Pada artikel ini, kita akan membahas secara lengkap pengertian Metode Horner, langkah-langkah penerapannya, serta berbagai contoh soal lengkap dengan pembahasannya. Mari kita mulai!
Cek di sini jika sedang mencari les matematika terdekat dari lokasi kamu
Apa Itu Metode Horner?
Dalam matematika, salah satu cara untuk menyelesaikan pembagian fungsi polinomial atau suku banyak adalah dengan Metode Horner. Sebelumnya, kamu mungkin sudah mengenal pembagian bersusun sebagai cara untuk membagi polinomial. Namun, metode ini memberikan pendekatan yang berbeda, dengan langkah-langkah yang lebih ringkas dan berfokus pada koefisien dari polinomial.
Metode Horner sering disebut juga dengan skema Horner. Ini adalah sebuah algoritma yang digunakan untuk mengevaluasi fungsi polinomial dengan cara yang lebih sistematis dan terstruktur. Dalam metode ini, yang perlu kamu perhatikan adalah koefisien dari polinomial
Metode ini biasanya digunakan untuk membagi suatu fungsi polinomial dengan bentuk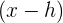 
atau 
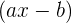. Dengan fokus pada koefisien, proses perhitungan bisa menjadi lebih cepat dan mudah dibandingkan dengan metode lain.
Pembagian Polinominal dengan Metode Horner
Untuk lebih memahami cara kerja Metode Horner, mari kita lihat langkah-langkahnya saat membagi polinomial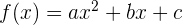 
dengan 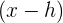. Berikut adalah Cara horner polinomial:
- Menuliskan Koefisien Secara Berurutan
Masukkan koefisien dari fungsi polinomial secara berurutan, mulai dari pangkat tertinggi hingga pangkat nol (konstanta). Sebagai contoh, untuk fungsi 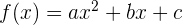, koefisiennya adalah 
.
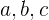- Substitusi Pembagi
Untuk pembagian dengan 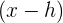, kita gunakan nilai 
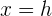. Artinya, setiap kali terdapat 
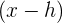, nilai 
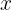akan digantikan dengan 
.
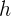- Menurunkan Koefisien Tertinggi
Bawa turun nilai koefisien pangkat tertinggi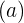 
, kemudian kalikan dengan nilai .
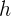- Penambahan dengan Koefisien Berikutnya
Hasil perkalian tersebut ditempatkan di bawah koefisien berikutnya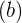 
. Kemudian, tambahkan kedua nilai tersebut untuk menghasilkan nilai baru.
- Ulangi Langkah Perhitungan
Ulangi langkah tersebut hingga mencapai koefisien terakhir dari fungsi polinomial. Hasil akhirnya akan memberikan nilai untuk hasil bagi dan sisa pembagian.
Contoh penerapan ini adalah ketika kita membagi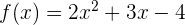 
dengan 
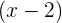. Kita akan memperoleh hasil bagi berupa polinomial dengan pangkat yang lebih rendah, serta sisa pembagian yang dapat digunakan untuk mengetahui apakah fungsi tersebut habis dibagi atau tidak.
Periksa di sini jika kamu ingin mempelajari rumus dilatasi dalam matematika.
Metode Horner (AX – B)
Bagaimana jika kita ingin membagi fungsi polinomial dengan bentuk pembagi 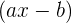? Misalnya, kita memiliki fungsi 
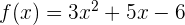dan ingin membaginya dengan 
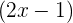. Langkah-langkahnya hampir sama seperti metode sebelumnya, namun ada beberapa penyesuaian:
- Masukkan koefisien secara berurutan.
- Gunakan nilai
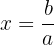untuk pembagi 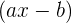. - Lakukan perhitungan dengan skema Horner hingga mendapatkan hasil bagi sementara.
- Setelah mendapatkan hasil bagi, perlu diingat untuk membaginya kembali dengan koefisien
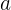dari pembagi .
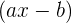Metode Horner Bersusun
Selanjutnya, kita juga memiliki Metode Horner Bersusun yang digunakan ketika pembagi terdiri dari dua faktor, seperti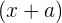 
dan 
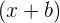. Metode ini memerlukan langkah perhitungan yang dilakukan secara bertahap, yaitu dengan membagi polinomial terlebih dahulu dengan satu faktor, kemudian melanjutkannya dengan faktor berikutnya.
Sebagai contoh, kita memiliki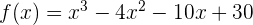 
dan ingin membaginya dengan 
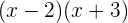. Langkah-langkahnya adalah sebagai berikut:
- Bagi
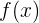terlebih dahulu dengan 
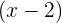, menggunakan metode Horner. - Gunakan hasil bagi dari langkah pertama sebagai polinomial baru, dan bagi kembali dengan
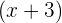. - Hitung sisanya pada setiap langkah untuk mengetahui hasil akhir pembagian.
Pelajari juga materi jangkauan antar kuartil
Metode Horner Kino
Metode ini diperkenalkan oleh Bapak Sukino, M.Sc., dalam bukunya. Metode ini menjadi populer di kalangan sekolah-sekolah sebagai alternatif penyelesaian pembagian polinomial yang lebih kompleks, terutama yang melibatkan faktor kuadrat.
Misalnya, untuk fungsi 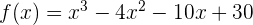yang dibagi dengan 
, yaitu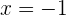 
dan 
.
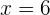Metode ini memerlukan pemahaman yang lebih mendalam, namun sangat berguna untuk kasus pembagian yang lebih rumit.
Berikut ini adalah beberapa contoh soal terkait Metode Horner beserta pembahasannya untuk membantu kamu memahami konsep ini dengan lebih baik:
Contoh Soal:
Diberikan polinomial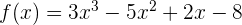 
. Tentukan hasil bagi dan sisanya ketika 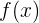dibagi dengan 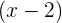menggunakan Metode Horner.
Pembahasan:
- Tuliskan koefisien dari polinomial:
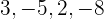. - Karena pembagi adalah 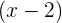, maka
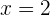. - Susun skema Horner:
- Bawa turun koefisien 3.
- Kalikan 3 dengan 2 (hasilnya 6), letakkan di bawah -5.
- Jumlahkan: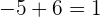 
.
- Kalikan 1 dengan 2 (hasilnya 2), letakkan di bawah 2.
- Jumlahkan: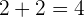 
.
- Kalikan 4 dengan 2 (hasilnya 8), letakkan di bawah -8.
- Jumlahkan: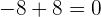 
.
Sehingga skema Horner-nya adalah:
2 | 3 -5 2 -8
| 6 2 8
-------------------
3 1 4 0
- Hasil bagi dari pembagian adalah
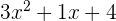. - Sisa pembagian adalah 0.
Jawaban:
Hasil bagi: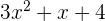 
Sisa: 0
Kesimpulan
Dengan memahami berbagai cara menggunakan Metode Horner untuk pembagian polinomial, kamu bisa memilih metode yang paling sesuai untuk setiap jenis soal. Jika kamu ingin belajar lebih dalam mengenai materi Metode Horner atau topik matematika lainnya, kamu bisa mencari tutor privat yang tepat melalui Superprof.
Dengan bimbingan tutor privat di Superprof, kamu bisa mendapatkan penjelasan yang lebih jelas, latihan soal yang terarah, dan bantuan langsung untuk memahami konsep-konsep yang sulit. Jangan lewatkan kesempatan ini untuk meningkatkan pemahamanmu. Temukan tutor matematika terbaik di Superprof sekarang juga, dan mulailah belajar dengan cara yang lebih efektif!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
