Tahukah Anda apa yang dimaksud dengan matriks? Dalam ilmu matematika, materi matriks termasuk salah satu materi yang menyenangkan. Meskipun sebagian besar siswa di sekolah kurang menyukai pelajaran matematika ini, perlu diketahui bahwa setidak sukanya Anda terhadap matematika, sulit bagi Anda untuk menghindari matematika dalam kehidupan sehari-hari. Sebagaimana kita ketahui, matematika merupakan bahasa simbol yang bersifat universal. Jika terdapat 7.000 bahasa berbeda di seluruh dunia, matematika contoh bahasa universal yang digunakan oleh seluruh penduduk dunia tanpa perbedaan. Matematika juga sulit untuk kita pisahkan dengan keseharian kita, karena konsep dan penggunaan matematika hampir di setiap aktifitas sehari-hari. Banyak masalah dalam kehidupan sehari-hari yang hanya dapat diselesaikan dengan model matematika.
Misalnya, pembuatan jurnal dan rapor yang mengandung banyak variabel, perhitungan populasi penduduk, rotasi dalam beberapa dimensi, kriptografi, persamaan reaksi, dll. Dan semua contoh yang disebutkan tersebut merupakan penggunaan konsep aljabar linier, yakni matriks. Bagi siswa jurusan komputer, matriks juga bukan sesuatu yang asing. Materi matriks dalam matematika digunakan dalam sistem komputer. Pemanfaatan matriks antara lain pada bidang keamanan komputer dan pemrograman yang membutuhkan array dalam ilmu komputer. Berbagai bidang IT tentu akan banyak mengoperasikan matriks matematika.
Yuk simak penjelasan berikut ini untuk mengetahui lebih jauh terkait, apa itu matriks, macam-macam matriks, dan matriks transpose!
Temukan disini les matematika surabaya
Definisi Matriks
Definisi matriks adalah sekumpulan bilangan atau angka yang disusun secara sistematis dalam baris dan kolom matriks, dan semua elemen matriks tersebut ditempatkan di dalam tanda kurung. Tanda kurung ini bisa berupa tanda kurung biasa "( )" atau tanda kurung siku "[ ]".
Secara umum, matriks diberi nama dengan huruf kapital, seperti A, B atau C. Matriks digunakan untuk mengorganisir data yang memiliki banyak variabel dalam bentuk yang lebih sederhana dan mudah dipahami. Matriks sering digunakan dalam berbagai aplikasi, baik itu dalam pemrograman komputer, sistem persamaan linear, analisis statistik, dan banyak lagi. Sebagai contoh, coba perhatikan data berikut ini!
Diketahui jumlah penjualan mobel dengan jenis A, B, C yang dijual dengan harga masing-masing adalah 146, 275, dan 528 (juta) pada kota-kota P, Q, R, sebagai berikut;
| Jenis Mobil | Harga Mobil (juta) | Jumlah penjualan pada tiap kota (unit) | ||
| Kota P | Kota Q | Kota R | ||
| A | 146 | 34 | 56 | 41 |
| B | 275 | 45 | 36 | 37 |
| C | 528 | 51 | 32 | 46 |
Data di atas dapat diubah dalam bentuk matriks yang lebih sederhana. Misalnya ;
Matrix harga mobil = 
Matrix penjualan mobil = 
Ordo Matriks dan Elemen Penting Lainnya
Salah satu elemen penting dalam matriks adalah ordo matriks, yang merujuk pada ukuran matriks, yaitu berapa banyak baris dan kolom yang dimiliki oleh matriks tersebut. Ordo matriks ini ditulis dalam bentuk m x n, di mana m adalah jumlah baris dan n adalah jumlah kolom.
Contoh ordo matriks 2x3 maka bisa dikatakan matriks A yang memiliki 2 baris dan 3 kolom.
Setiap angka atau bilangan yang ada dalam matriks disebut sebagai elemen matriks. Elemen-elemen ini diidentifikasi dengan indeks yang menunjukkan posisinya dalam baris dan kolom. Sebagai contoh, jika kita memiliki matriks A sebagai berikut:
A =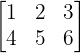 
Maka, elemen matriks A yang terletak di baris ke-1 dan kolom ke-2 adalah angka 2, yang bisa ditulis dengan notasi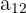 
, di mana angka pertama adalah baris, dan angka kedua adalah kolom.
Pahami juga pengertian fungsi dan invers dalam matematika!
Macam-Macam Matriks
Ada beberapa jenis matriks yang perlu Anda ketahui. Berikut ini adalah beberapa jenis matriks yang biasa ditemui:
Matriks Baris
Matriks baris adalah jenis matriks yang hanya terdiri dari satu baris saja. Matriks ini sangat sederhana dan berguna untuk mewakili data dalam bentuk satu dimensi horizontal. Contohnya, matriks baris 1x3 adalah:
A =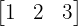 
Matriks Kolom
Matriks kolom adalah kebalikan dari matriks baris, di mana matriks ini hanya terdiri dari satu kolom saja. Matriks kolom digunakan untuk menyusun data dalam bentuk satu dimensi vertikal. Contoh matriks kolom 3x1 adalah:
B =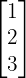 
Kenali juga rumus peluang dan contoh soalnya berikut ini!
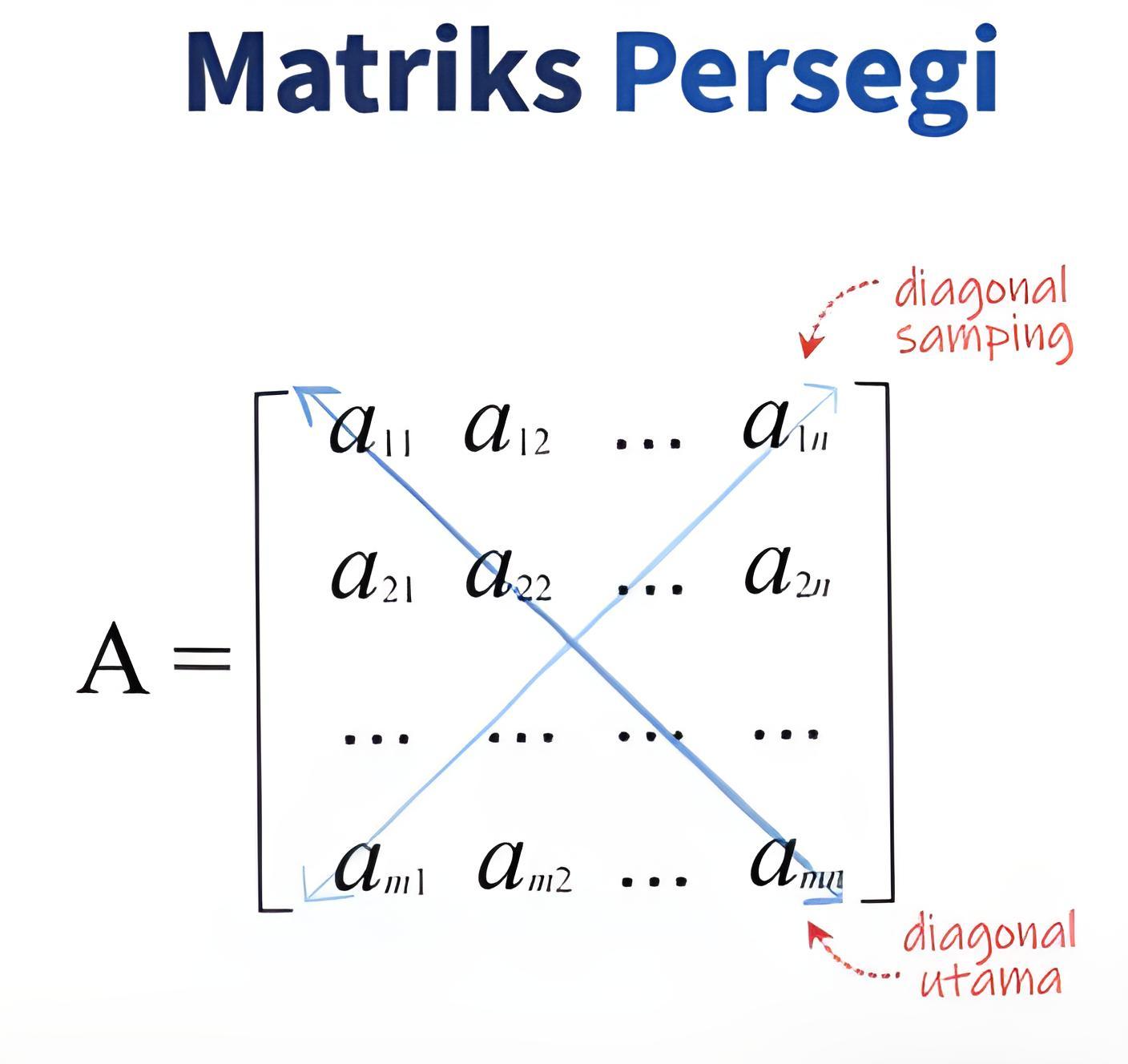
Matriks Persegi
Matriks persegi adalah matriks yang memiliki jumlah baris dan kolom yang sama. Ini berarti jumlah barisnya sama dengan jumlah kolomnya. Sebagai contoh, matriks 3x3 adalah matriks persegi:
C = 
Pada matriks persegi, kita mengenal istilah diagonal utama yaitu elemen-elemen matriks yang terletak pada posisi baris dan kolom yang sama, seperti angka 1, 5, dan 9 pada contoh matriks di atas. Selain diagonal utama, ada juga yang disebut dengan diagonal samping matriks atau diagonal kedua yang berjalan dari kiri bawah ke kanan atas.
Matriks Diagonal
Matriks diagonal adalah matriks persegi di mana semua elemen selain elemen diagonal utamanya bernilai nol. Sebagai contoh:
D = 
Pada matriks ini, hanya elemen-elemen yang ada pada diagonal utama yang memiliki nilai (3, 5, dan 7), sementara elemen lainnya adalah nol.
Matriks Identitas
Matriks identitas adalah matriks persegi yang memiliki elemen pada diagonal utama yang bernilai satu, dan semua elemen lainnya bernilai nol. Sebagai contoh, matriks identitas 3x3 adalah:
I = 
Matriks Nol
Matriks nol adalah matriks yang semua elemennya bernilai nol. Ini adalah bentuk matriks yang sangat sederhana. Contoh matriks nol 3x3 adalah:
O = 
Jika Anda belum tahu tentang aturan dasar trigonometri, Anda wajib membaca artikel ini!
Transpose Matriks
Transpose matriks adalah operasi yang melibatkan pertukaran antara baris dan kolom dalam suatu matriks. Jika Anda memiliki matriks A 2x2, maka transpose matriks 2x2 A, yang ditulis sebagai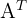 
, diperoleh dengan menukar elemen-elemen baris menjadi kolom dan sebaliknya.
Sebagai contoh, jika matriks A adalah:
A = 
Maka, rumus matriks transpose A, dapat ditulis sebagai 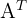, adalah:
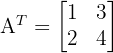
Dalam hal ini, elemen-elemen baris pertama dan kedua pada matriks A bertukar menjadi kolom pertama dan kedua pada matriks .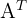
Apakah menurut Anda matriks matematika sama mudahnya dengan materi tentang persamaan lingkaran?
Matrix adalah konsep dasar yang sangat penting dalam matematika dan sering digunakan dalam berbagai bidang ilmu. Dengan memahami cara kerja matriks dan operasi-operasi yang bisa dilakukan terhadapnya, Anda akan lebih mudah menyelesaikan berbagai masalah matematika yang kompleks. Jika Anda sedang kesulitan belajar tentang matriks atau topik matematika lainnya, les privat matematika bisa menjadi pilihan yang tepat. Dengan bimbingan dari pengajar yang berpengalaman, Anda bisa belajar lebih cepat dan menguasai materi dengan cara yang tepat. Jangan ragu untuk mencari les privat matematika di Superprof dan mulai perjalanan belajar Anda sekarang juga! Tetap pertimbangkan juga kunjungan ke tempat les matematika yang sesuai dengan kebutuhan Anda.
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
