Apakah Anda pernah menghitung jarak dari rumah ke pasar? Pernahkah Anda berpikir mengapa jarak tersebut selalu bernilai positif? Mengapa nilai tersebut tidak pernah minus? Hal ini tentunya sering kita alami dalam kehidupan sehari-hari tanpa menyadarinya. Untuk memahami hal ini dengan lebih baik, Anda perlu mengenal konsep yang dikenal dengan nama nilai mutlak.
Dalam matematika, bilangan mutlak adalah konsep yang digunakan untuk menggambarkan suatu bilangan tanpa memperhatikan arahnya, yang berarti selalu bernilai positif atau nol. Artikel ini akan menjelaskan secara mendalam mengenai nilai mutlak, mulai dari pengertian dasar, sifat-sifatnya, hingga penerapannya dalam kehidupan sehari-hari.

Apa Yang Dimaksud Dengan Absolut?
Sebelum kita melangkah lebih jauh dalam memahami nilai mutlak, penting untuk mengetahui terlebih dahulu apa itu absolut. Konsep absolut banyak digunakan dalam berbagai bidang, baik dalam hukum, politik, ekonomi, dan juga matematika.
Dalam Kamus Besar Bahasa Indonesia (KBBI), absolut memiliki arti yang dekat dengan mutlak atau tidak terbatas. Lebih spesifik lagi, arti absolut adalah sesuatu yang sepenuhnya, tanpa syarat, tidak dapat diragukan lagi, atau bersifat murni.
Dalam bahasa Inggris, kata absolute adalah sesuatu yang "free from imperfection" (bebas dari ketidaksempurnaan), "complete" (lengkap), atau "perfect" (sempurna). Mutlak artinya juga adalah "not mixed" atau "pure" yang berarti murni. Dengan kata lain, konsep absolut dapat menggambarkan suatu kondisi yang tidak terpengaruh atau tidak terbagi oleh faktor luar.
Sebagai contoh dalam hukum, dalam pengadilan, terdapat istilah kekuasaan absolut. Kekuasaan absolut adalah kewenangan hakim untuk memutuskan suatu perkara tanpa adanya campur tangan pihak lain.
Kekuasaan ini disebut sebagai kekuasaan kehakiman atribusi (attributie van rechtsmacht), yang merupakan kewenangan mutlak suatu pengadilan untuk menangani jenis perkara tertentu. Artinya, hanya pengadilan tersebut yang memiliki wewenang untuk mengadili perkara tersebut, tidak bisa digantikan oleh pengadilan lain.
Cek di sini untuk mempelajari standar deviasi
Pengertian Nilai Mutlak Dalam Matematika

Setelah memahami pengertian absolut, kita bisa beralih untuk membahas pengertian nilai mutlak. Secara sederhana, nilai absolut artinya merujuk pada jarak suatu bilangan terhadap angka nol di dalam garis bilangan.
Ini berarti nilai mutlak akan selalu bernilai positif, tanpa mempedulikan apakah angka yang dimaksud adalah angka positif atau negatif. Dengan kata lain, nilai mutlak suatu bilangan akan menggambarkan seberapa jauh bilangan tersebut dari nol, tanpa memperhatikan arah (apakah ke kiri atau ke kanan).
Nilai absolute artinya juga disebut sebagai jarak absolut atau jarak sebenarnya dari suatu bilangan, karena tidak memandang arah atau tanda dari bilangan tersebut.
Sebagai contoh, Anda tidak mungkin mengatakan umur seorang bayi dalam kandungan adalah -3 bulan, karena bayi tersebut belum lahir. Sebagai gantinya, usia bayi tersebut akan dihitung dengan umur kandungan, seperti “bayi tersebut berusia 6 bulan”.
Secara matematis, kita dapat menyatakan rumus mutlak adalah dengan simbol |x| yang berarti nilai mutlak dari x. Nilai mutlak ini dapat dijelaskan sebagai berikut:
|x| = x jika x ≥ 0
|x| = -x jika x < 0
Ciri-Ciri Nilai Mutlak
Dalam konsep nilai mutlak, ada beberapa sifat mutlak yang perlu diketahui agar lebih mudah memahami bagaimana nilai absolute bekerja. Berikut adalah lima sifat dasar dalam nilai mutlak:
∣a∣ ≥ 0
Sifat pertama ini menyatakan bahwa nilai mutlak dari suatu bilangan selalu lebih besar atau sama dengan nol. Ini berarti nilai mutlak tidak pernah bernilai negatif, meskipun angka aslinya adalah negatif. Dengan kata lain, nilai mutlak akan selalu bernilai positif atau nol.
∣−a∣ = ∣a∣
Sifat kedua ini menyatakan bahwa nilai mutlak dari -a adalah sama dengan nilai mutlak dari a. Artinya, jika suatu bilangan memiliki nilai negatif, maka nilai mutlaknya akan sama dengan nilai mutlak dari angka positif yang sama. Sebagai contoh, |−1| = |1| = 1. Hal ini dikarenakan nilai mutlak menghitung jarak dari nol, tanpa memperhatikan tanda negatif.
∣a∣ = √a²
Sifat ini menyatakan bahwa nilai mutlak dari a sama dengan akar kuadrat dari a pangkat dua. Konsep ini menyiratkan bahwa kita tidak perlu peduli apakah angka tersebut positif atau negatif.
∣a·b∣ = ∣a∣·∣b∣
Sifat selanjutnya adalah bahwa nilai mutlak dari hasil perkalian dua bilangan adalah hasil kali dari nilai mutlak masing-masing bilangan. Sebagai contoh, jika a = 5 dan b = -3, maka nilai mutlak dari 5 × -3 adalah sama dengan |5| × |-3| = 5 × 3 = 15.
∣a/b∣ = (∣a∣)/(∣b∣), b ≠ 0
Sifat ini berlaku saat kita membagi dua bilangan. Nilai mutlak dari hasil pembagian dua bilangan adalah hasil pembagian dari nilai mutlak masing-masing bilangan tersebut, dengan syarat pembaginya tidak boleh nol.
Cek di sini untuk mempelajari garis singgung lingkaran
Membuat Grafik Fungsi Nilai Mutlak
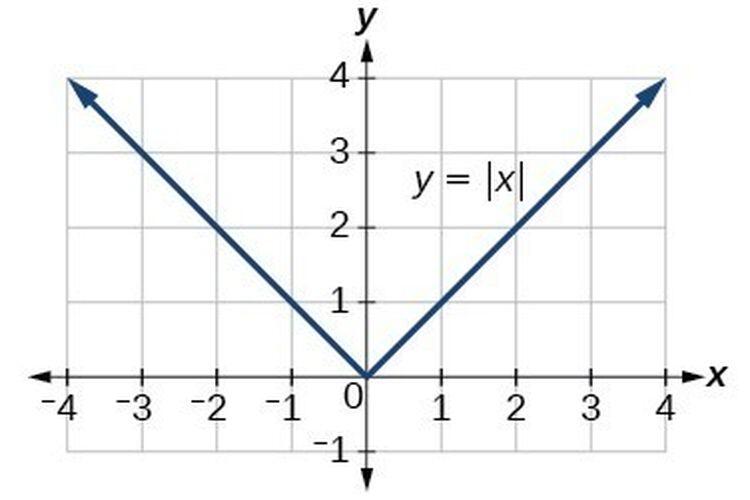
Salah satu cara paling mudah untuk memahami konsep nilai mutlak adalah dengan membuat grafik fungsi nilai mutlak. Dengan menggambar grafik ini, kita dapat lebih mudah melihat bagaimana nilai mutlak berfungsi dalam berbagai bilangan. Berikut adalah langkah-langkah untuk menggambar grafik fungsi mutlak:
- Buat tabel fungsi nilai mutlak dengan menggunakan titik bantu
Tentukan beberapa nilai untuk x, kemudian hitung nilai mutlaknya. Pilih titik yang bervariasi, baik yang positif maupun negatif. - Isi tabel fungsi nilai mutlak sesuai dengan definisi nilai mutlak
Hitung nilai mutlak dari setiap nilai x yang telah dipilih. Sebagai contoh, untuk x = -3, maka nilai mutlaknya adalah 3, sedangkan untuk x = 4, nilai mutlaknya adalah 4. - Sajikan titik-titik yang diperoleh dengan menggunakan sistem koordinat kartesius
Setelah mendapatkan nilai mutlak untuk setiap titik, plot titik-titik tersebut pada grafik dan hubungkan titik-titik tersebut untuk membentuk grafik.
Hasil dari grafik ini akan membentuk garis berbentuk "V" yang simetris terhadap sumbu y, dengan titik puncaknya di nol (0). Grafik ini menggambarkan bahwa nilai mutlak mengabaikan arah dan hanya memperhitungkan jarak dari nol.
Periksa di sini untuk mempelajari barisan dan deret matematika

Harga Mutlak dalam Kehidupan Sehari-hari

Nilai mutlak bukan hanya terbatas pada dunia matematika. Konsep ini juga dapat diterapkan dalam kehidupan sehari-hari. Contohnya, ketika Anda mengemudi, kecepatan kendaraan Anda adalah nilai mutlak yang menunjukkan seberapa jauh kendaraan Anda bergerak dari kecepatan nol, tanpa memperhitungkan arah pergerakan.
Pentingnya Memahami Nilai Mutlak
Memahami nilai mutlak penting karena membantu kita memahami jarak absolut atau perbedaan antara dua titik dalam konteks matematika dan kehidupan nyata. Dalam matematika, nilai mutlak sering digunakan dalam pemecahan masalah aljabar, geometri, dan analisis.
Dalam kehidupan sehari-hari, pemahaman tentang nilai mutlak dapat membantu Anda membuat keputusan yang lebih tepat. Misalnya, ketika membandingkan penawaran harga barang, mengetahui harga mutlaknya akan membantu Anda menilai mana yang lebih ekonomis.
Periksa di sini untuk mempelajari translasi matematika
Contoh Soal
Soal 1:
Tentukan nilai mutlak dari -8.
Jawaban:
Nilai mutlak dari -8 adalah ∣−8∣ = 8
Soal 2:
Jika
∣x∣ = 5, tentukan nilai dari x.
Jawaban:
Karena nilai mutlak dari x adalah 5, maka x bisa sama dengan 5 atau -5. Jadi, solusinya adalah x=5 atau x=−5.
Dari contoh diatas dapatkah Anda menyebutkan bilangan yang memiliki nilai mutlak 7 adalah apa saja?
Manfaat Konsep Nilai Mutlak dalam Matematika
- Kemudahan Perhitungan: Konsep nilai mutlak membantu menyederhanakan perhitungan matematika dengan memungkinkan kita untuk fokus pada jarak absolut antara dua titik atau nilai.
- Pemecahan Masalah: Nilai mutlak membantu dalam pemecahan masalah yang melibatkan perbandingan, perhitungan jarak, dan penentuan solusi dalam berbagai konteks matematika.
- Pemahaman Konsep: Memahami nilai mutlak membantu memperdalam pemahaman tentang konsep-konsep matematika yang lebih kompleks, seperti fungsi, persamaan, dan ketidaksetaraan.
Dengan memahami konsep nilai mutlak dalam matematika, Anda akan memiliki dasar yang kuat untuk menjelajahi berbagai bidang matematika dengan lebih percaya diri dan berhasil. Jadi, jangan ragu untuk mempelajari lebih lanjut tentang konsep ini dan menerapkannya dalam pemecahan masalah matematika yang lebih kompleks!
Cek di sini untuk les online matematika
Manfaat dari Memahami Nilai Mutlak Untuk Siswa
1. Pemecahan Masalah yang Efektif: Dengan memahami nilai mutlak, Anda dapat dengan cepat menyelesaikan masalah matematika yang melibatkan perhitungan jarak absolut.
2. Pengambilan Keputusan yang Lebih Baik: Dalam kehidupan sehari-hari, pemahaman tentang nilai mutlak memungkinkan Anda membuat keputusan yang lebih rasional dan tepat, terutama dalam hal perbandingan antara dua pilihan.
3. Peningkatan Keterampilan Analitis: Memahami nilai mutlak membantu meningkatkan keterampilan analitis Anda, karena Anda belajar untuk memisahkan informasi penting dari yang tidak penting dalam konteks perhitungan.
Penerapan Nilai Mutlak dalam Berbagai Bidang
1. Matematika: Dalam matematika, nilai mutlak digunakan dalam berbagai konsep, termasuk fungsi nilai mutlak, ketidaksetaraan nilai mutlak, dan pemecahan masalah geometri.
2. Fisika: Dalam fisika, nilai mutlak digunakan untuk mengukur jarak absolut antara dua titik dalam ruang atau waktu.
3. Ekonomi: Dalam ekonomi, nilai mutlak sering digunakan untuk membandingkan harga, tingkat pertumbuhan, atau perubahan dalam data ekonomi.
Periksa di sini jika sedang mencari tempat les matematika
Ayo Belajar Bersama Superprof!
Untuk memperdalam pemahaman Anda tentang nilai mutlak dan konsep matematika lainnya, bergabunglah dengan Superprof! Superprof menyediakan tutor profesional yang siap membantu Anda memahami konsep-konsep matematika dengan cara yang menyenangkan dan efektif. Jangan ragu untuk memanfaatkan kesempatan ini untuk meningkatkan pemahaman Anda dalam matematika dan bidang lainnya. Mulailah perjalanan pendidikan Anda hari ini bersama Superprof!
Dengan memahami nilai mutlak, Anda akan memiliki landasan yang kuat untuk memecahkan masalah matematika yang lebih kompleks dan membuat keputusan yang lebih tepat dalam kehidupan sehari-hari. Jadi, jangan ragu untuk melangkah maju dan eksplorasi dunia matematika lebih dalam bersama Superprof!
Ringkaskan dengan AI















