Dalam dunia statistika, memahami konsep jangkauan antar kuartil sangat penting untuk menganalisis penyebaran data. Jangkauan ini berkaitan dengan seberapa tersebar nilai-nilai dalam suatu kumpulan data di antara kuartil-kuartil tertentu. Artikel ini akan mengulas secara mendalam tentang jangkauan antar kuartil, simpangan kuartil, termasuk penerapan dalam data tunggal dan data kelompok, serta menyajikan berbagai rumus untuk membantu Anda memahami topik ini dengan lebih baik.
Cek di sini jika sedang mencari les matematika terdekat di Bandung

Apa itu Jangkauan Antar Kuartil?
Jangkauan antar kuartil adalah ukuran penyebaran data yang dihitung dengan mencari selisih antara kuartil ketiga (Q3) dan kuartil pertama (Q1). Dengan kata lain, ini menunjukkan seberapa tersebar data di bagian tengah distribusi. Jangkauan antar kuartil menghilangkan pengaruh ekstrem dari data dengan hanya fokus pada 50% data di tengah, sehingga lebih representatif daripada jangkauan total.
Rumus jangkauan antar kuartil dapat dirumuskan sebagai:
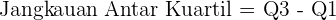
Di sini, Q1 adalah kuartil pertama (25% data berada di bawahnya), dan Q3 adalah kuartil ketiga (75% data berada di bawahnya). Rumus ini membantu kita memahami variasi nilai di tengah kumpulan data dan mengabaikan outlier di bagian ekstrem.
Cara menghitung jangkauan kuartil:
Sebelum menghitung jangkauan antar kuartil, Anda harus menentukan Q1, Q2 (median), dan Q3. Berikut adalah langkah-langkah cara menghitung jangkauan kuartil:
1. Urutkan data dari yang terkecil hingga terbesar.
2. Tentukan nilai median (Q2), yang membagi data menjadi dua bagian yang sama.
3. Q1 (Kuartil Pertama) adalah median dari bagian bawah (data di bawah Q2).
4. Q3 (Kuartil Ketiga) adalah median dari bagian atas (data di atas Q2).
5. Gunakan rumus:
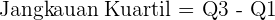
Jangkauan kuartil ini bisa digunakan untuk menemukan simpangan kuartil, yaitu setengah dari jangkauan antar kuartil.
Cek di sini jika ingin mempelajari metode horner pada matematika
Simpangan Kuartil
Simpangan kuartil atau juga disebut sebagai rentang semi-interkuartil, adalah setengah dari jangkauan antar kuartil. Simpangan kuartil menunjukkan seberapa tersebar data di sekitar nilai tengah distribusi, dan mengukur rata-rata jarak antara Q1 dan Q3.
Rumus simpangan kuartil adalah:
Simpangan Kuartil = Q3 - Q1 / 2
Dengan menggunakan rumus ini, kita bisa melihat seberapa konsisten atau beragam data yang dianalisis.
Periksa di sini jika kamu ingin mempelajari rumus dilatasi dalam matematika.

Simpangan Kuartil pada Data Tunggal
Pada simpangan kuartil data tunggal, data disajikan dalam bentuk kumpulan nilai-nilai individu. Berikut contoh perhitungan simpangan kuartil untuk data tunggal:
Contoh Soal:
Data berikut disajikan: 3, 5, 7, 8, 12, 15, 18, 20, 25.
Langkah-langkah:
1. Urutkan data: 3, 5, 7, 8, 12, 15, 18, 20, 25.
2. Tentukan Q2 (Median):
Median adalah 12 (karena ini adalah nilai tengah).
3. Cari Q1: Median dari 3, 5, 7, 8 = 6.
4. Cari Q3: Median dari 15, 18, 20, 25 = 19.
Hitung Jangkauan Antar Kuartil:
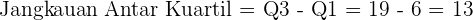
Hitung Simpangan Kuartil:
Simpangan Kuartil = Q3 - Q1 / 2 = 13/2 = 6,5
Hasil ini menunjukkan bahwa simpangan kuartil untuk data tunggal tersebut adalah 6,5.
Periksa di sini jika kamu ingin mempelajari fungsi kuadrat
Simpangan Kuartil pada Data Kelompok
Ketika data diberikan dalam bentuk kelompok, seperti dalam tabel distribusi frekuensi, cara menghitung simpangan kuartil data kelompok sedikit berbeda. Kita perlu menggunakan rumus interpolasi untuk menentukan Q1 dan Q3 dengan lebih akurat.
Rumus Jangkauan Kuartil pada Data Kelompok:
Untuk mencari Q1 dan Q3, kita menggunakan rumus interpolasi:
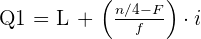
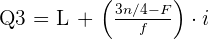
Keterangan:
- L = Batas bawah kelas kuartil
- n = Total frekuensi
- F = Frekuensi kumulatif sebelum kelas kuartil
- f = Frekuensi kelas kuartil
- i = Interval kelas
Setelah menghitung Q1 dan Q3, kita dapat menggunakan rumus simpangan kuartil yang sama seperti pada data tunggal:
Simpangan Kuartil = Q3 - Q1 / 2
Contoh Simpangan Kuartil Data Kelompok
Misalkan, data tinggi badan siswa dibagi dalam interval sebagai berikut:
| Interval Tinggi (cm) | Frekuensi |
|---|---|
| 150 – 155 | 5 |
| 156 – 161 | 10 |
| 162 – 167 | 15 |
| 168 – 173 | 20 |
| 174 – 179 | 10 |
Langkah-langkah:
1. Hitung frekuensi kumulatif.
2. Cari Q1 dan Q3 dengan rumus interpolasi.
3. Gunakan rumus jangkauan kuartil dan simpangan kuartil seperti sebelumnya.
Misalkan hasil perhitungan adalah Q1 = 156,5 cm dan Q3 = 170,2 cm.
Hitung Jangkauan Antar Kuartil:
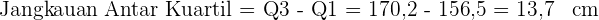
Hitung Simpangan Kuartil:
Simpangan Kuartil = 13,7/2 = 6,85 cm
Dengan demikian, simpangan kuartil untuk data kelompok tersebut adalah 6,85 cm.
Dalam matematika, jangkauan antar kuartil dan simpangan kuartil adalah alat penting untuk memahami variasi dan penyebaran data. Simpangan kuartil data tunggal dan simpangan kuartil data kelompok mengikuti prinsip serupa tetapi memerlukan pendekatan berbeda dalam penghitungan. Dengan menggunakan rumus jangkauan antar kuartil dan rumus jangkauan kuartil, kita bisa menganalisis data dengan lebih efektif dan mengabaikan pengaruh outlier.
Jika Anda merasa pusing dengan materi simpangan kuartil atau kesulitan memahami Pelajaran matematika lainnya, jangan khawatir! Dapatkan bantuan langsung dari tutor berpengalaman dengan mengikuti les privat di Superprof. Bersama tutor privat, Anda bisa belajar lebih fokus dan memahami materi dengan lebih cepat. Yuk, temukan tutor terbaik Anda di Superprof sekarang juga dan atasi semua kesulitan belajar dengan mudah!
Ringkaskan dengan AI















