“Tetapi menurut saya, semua hal di alam terjadi secara matematis.” ― Rene Decartes
Interval adalah bagian menarik dari aljabar. Aritmatika interval dapat digunakan untuk menemukan semua angka real antara dua bilangan dalam satu himpunan.
Superprof hadir dengan sedikit kursus penyegar untuk Anda. Seperti yang akan Anda lihat, interval mengharuskan jenis pemikiran tertentu.

Apa Itu Interval Dalam Matematika
Interval adalah rentang angka antara dua angka tertentu, yang mencakup semua bilangan real di antara angka-angka tersebut. Dalam matematika, interval biasanya digunakan untuk menunjukkan set angka yang terletak antara dua batas, yang bisa termasuk atau tidak termasuk angka batas tersebut.
Cek di sini jika sedang mencari les privat matematika jakarta timur
Cek di sini jika sedang mencari les matematika di bandung

Pelajari lebih lanjut tentang matematika.
Kita menggunakan simbol R untuk himpunan bilangan real. Kita menyebut titik akhir dari himpunan ini a dan b.
Mari kita lihat [4 ; 6]. Ini menunjukkan semua bilangan real 4 ≤ x ≤ 6. Ini mencakup angka 4, 5, dan 6, karena semuanya lebih besar dari atau sama dengan 4 dan lebih kecil dari atau sama dengan 6.
Ada beberapa jenis interval berbeda.
- Interval tertutup
- Interval terbuka
- Interval setengah terbuka
- Interval tak terbatas
Notasi Interval dalam Matematika
Notasi interval adalah cara untuk menuliskan rentang angka yang mencakup semua bilangan real di antara dua angka tertentu. Notasi ini digunakan untuk menyederhanakan representasi himpunan bilangan dan membantu dalam pemahaman serta penyelesaian masalah matematika yang melibatkan interval. Ada beberapa jenis notasi interval yang sering digunakan dalam matematika, yaitu interval terbuka, tertutup, dan setengah terbuka. Berikut adalah penjelasan mendetail tentang masing-masing notasi interval.
Jenis-jenis Notasi Interval
1. Interval Terbuka
- Notasi: (a, b)
- Deskripsi: Interval terbuka mencakup semua bilangan real antara a dan b, tetapi tidak termasuk a dan b.
- Contoh: (2, 5) mencakup semua bilangan yang lebih besar dari 2 dan lebih kecil dari 5, seperti 2.1, 3, 4.9, tetapi tidak termasuk 2 dan 5.
2. Interval Tertutup
- Notasi: [a, b]
- Deskripsi: Interval tertutup mencakup semua bilangan real antara a dan b, termasuk a dan b.
- Contoh: [2, 5] mencakup semua bilangan dari 2 hingga 5, termasuk 2 dan 5, seperti 2, 3, 4, 5.
3. Interval Setengah Terbuka (atau Setengah Tertutup)
- Notasi: (a, b] atau [a, b)
- Deskripsi: Interval matematika setengah terbuka mencakup semua bilangan real antara a dan b, tetapi hanya salah satu dari a atau b yang termasuk.
- (a, b]: Mencakup bilangan real antara a dan b, termasuk b tetapi tidak termasuk a.
- [a, b): Mencakup bilangan real antara a dan b, termasuk a tetapi tidak termasuk b.
- Contoh:
- (2, 5] mencakup semua bilangan lebih besar dari 2 dan kurang dari atau sama dengan 5, seperti 2.1, 3, 4.9, 5 tetapi tidak termasuk 2.
- [2, 5) mencakup semua bilangan dari 2 hingga kurang dari 5, seperti 2, 3, 4, 4.9 tetapi tidak termasuk 5.
4. Interval Tak Terbatas
- Notasi: (-∞, a), (a, ∞), (-∞, a], atau [a, ∞)
- Deskripsi: Interval ini melibatkan nilai tak hingga di salah satu atau kedua ujungnya.
- (-∞, a): Mencakup semua bilangan real yang lebih kecil dari a.
- (a, ∞): Mencakup semua bilangan real yang lebih besar dari a.
- (-∞, a]: Mencakup semua bilangan real yang lebih kecil atau sama dengan a.
- [a, ∞): Mencakup semua bilangan real yang lebih besar atau sama dengan a.
- Contoh:
- (-∞, 3) mencakup semua bilangan yang lebih kecil dari 3.
- (5, ∞) mencakup semua bilangan yang lebih besar dari 5.
- (-∞, 3] mencakup semua bilangan yang lebih kecil atau sama dengan 3.
- [5, ∞) mencakup semua bilangan yang lebih besar atau sama dengan 5.
Penggunaan Notasi Interval dalam Garis Bilangan
Notasi interval sering digunakan untuk menggambarkan himpunan bilangan pada garis bilangan. Garis bilangan adalah representasi visual dari bilangan real, di mana setiap titik pada garis tersebut mewakili bilangan real tertentu. Berikut adalah cara menggambarkan interval pada garis bilangan:
1. Interval Terbuka (a, b):
- Digambarkan dengan garis tanpa ujung yang terisi, yaitu lingkaran kosong di titik a dan b.
- Contoh: (2, 5) akan digambarkan sebagai garis dari 2 hingga 5 dengan lingkaran kosong di kedua ujungnya.
2. Interval Tertutup [a, b]:
- Digambarkan dengan garis dengan ujung yang terisi, yaitu lingkaran penuh di titik a dan b.
- Contoh: [2, 5] akan digambarkan sebagai garis dari 2 hingga 5 dengan lingkaran penuh di kedua ujungnya.
3. Interval Setengah Terbuka (a, b] atau [a, b):
- Digambarkan dengan satu ujung lingkaran kosong dan satu ujung lingkaran penuh.
- Contoh:
- (2, 5] akan digambarkan sebagai garis dari 2 hingga 5 dengan lingkaran kosong di 2 dan lingkaran penuh di 5.
- [2, 5) akan digambarkan sebagai garis dari 2 hingga 5 dengan lingkaran penuh di 2 dan lingkaran kosong di 5.
Pelajari cara menghitung median.
Cara Menulis Interval
Batasan interval ditunjukkan dengan tanda kurung. Untuk interval terbuka dan setengah terbuka, tanda kurung siku digunakan: [a ; b] untuk interval terbuka dan [a ; b dan a ; b] untuk interval setengah terbuka.

Ketika menulis interval, interval perlu ditulis dalam urutan yang naik. Interval tidak pernah ditulis dalam urutan yang menurun. Ketika tanda kurung ditutup, itu artinya setiap titik batas disertakan. Ketika tanda kurung terbuka, itu artinya titik akhirnya tidak disertakan.
Berikut adalah himpunan bilangan bulat {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9}. Himpunan ini mencakup semua bilangan bulat mulai 0 hingga 9 inklusif.
Untuk himpunan abstrak, Anda perlu menggunakan huruf. Ini sangat umum dalam aljabar.
Ada beberapa penggunaan umum:
- N menunjukkan bilangan bulat asli.
- Z menunjuk bilangan relatif.
- D menunjuk desimal.
- Q menunjukkan bilangan rasional.
- R menunjukkan bilangan real.
- I menunjukkan perpotongan antara dua himpunan.
- U menunjukkan gabungan dua himpunan.
Anda juga akan melihat tanda matematika untuk menunjukkan dua himpunan bilangan real dan bagaimana mereka berinteraksi.
Tanda ini mungkin tampak cukup rumit dan abstrak awalnya, tapi dengan latihan, Anda akan mengetahui bahwa tanda ini cukup sederhana dan mudah digunakan.
Tanda-tanda tersebut dapat berguna untuk memvisualisasikan data matematis. Ini dapat digunakan untuk melihat bagaimana berbagai interval berinteraksi.
Teruslah mencoba berbagai latihan sampai Anda menguasainya. Interval dapat mengehemat banyak waktu.
Berikut adalah tabel ringkas yang merangkumnya:
| Tanda | Arti |
|---|---|
| ∈ | milik |
| ∉ | bukan milik |
| ∞ | tidak terbatas |
| ∩ | irisan |
| ∪ | gabungan |
| ≠ | tidak sama dengan |
| ≤ | kurang dari sama dengan |
| ≥ | lebih dari sama dengan |
| < | kurang dari |
| > | lebih dari |
Lihat artikel kami tentang algoritma.
Rumus Interval
Rumus interval biasanya digunakan dalam konteks statistik dan analisis data. Salah satu aplikasi yang umum adalah dalam menghitung interval kepercayaan (confidence interval). Interval kepercayaan memberikan rentang nilai yang diperkirakan mengandung parameter populasi tertentu dengan tingkat kepercayaan tertentu.
Rumus umum untuk nilai interval adalah:
\[ CI = \bar{x} \pm (Z \times \frac{\sigma}{\sqrt{n}}) \]
Di mana:
- \( \bar{x} \) adalah mean sampel.
- \( Z \) adalah nilai dari distribusi normal standar yang sesuai dengan tingkat kepercayaan.
- \( \sigma \) adalah deviasi standar populasi.
- \( n \) adalah ukuran sampel.
Dalam konteks analisis data, interval juga sering digunakan saat menyusun tabel distribusi frekuensi. Tabel distribusi frekuensi berfungsi untuk mengelompokkan data dalam bentuk interval agar pola persebaran data lebih mudah dipahami. Misalnya, ketika mengolah data nilai siswa, rentang nilai dapat dibagi ke dalam interval seperti 60–69, 70–79, atau 80–89. Dengan cara ini, setiap interval menunjukkan jumlah data yang berada di dalamnya, sehingga memudahkan pengamatan terhadap kecenderungan, sebaran, dan karakteristik data. Penggunaan interval dalam tabel distribusi frekuensi membantu menyederhanakan data yang kompleks dan sangat relevan dalam statistik dasar maupun analisis matematika.
Skala Interval
Banyak yang masih penasaran tentang “Apa itu skala interval?”. Dalam pembahasan statistika sendiri, penting juga memahami bahwa skala interval adalah salah satu jenis skala pengukuran data yang menggunakan rentang angka dengan jarak (interval) yang sama antar nilai. Skala interval memungkinkan perbandingan antar data secara lebih akurat karena setiap selisih antara dua nilai memiliki makna yang konsisten. Contohnya dapat ditemukan pada pengukuran suhu dalam Celsius atau Fahrenheit, di mana perbedaan 10°C dan 20°C sama dengan perbedaan 20°C dan 30°C. Konsep interval dalam skala interval sangat berkaitan dengan penggunaan interval pada garis bilangan maupun tabel distribusi frekuensi, karena semuanya berfungsi untuk menggambarkan rentang nilai secara terstruktur dan terukur.
Dalam statistika deskriptif, interval kelas adalah batas atas dan batas bawah yang menentukan pengelompokan data ke dalam kelas-kelas tertentu. Interval kelas berfungsi untuk menyederhanakan data yang jumlahnya besar agar pola distribusi lebih mudah dibaca. Misalnya, ketika data nilai siswa sangat beragam, interval kelas seperti 50–59, 60–69, hingga 90–99 membantu merapikan data menjadi kelompok yang lebih terstruktur. Penentuan interval kelas yang tepat juga berpengaruh langsung pada penyusunan tabel distribusi frekuensi, karena setiap kelas akan menunjukkan banyaknya data yang berada dalam rentang tersebut. Dengan demikian, interval kelas memegang peran penting dalam analisis statistik berbasis interval.
Skala interval digunakan untuk mengukur data yang jaraknya antar nilai pasti sama, tetapi tidak memiliki titik nol absolut. Artinya, nilai “nol” pada skala interval bukan berarti “tidak ada”.
Beberapa contoh skala interval:
- Suhu dalam Celcius atau Fahrenheit
Misalnya: 10°C, 20°C, 30°C.
Selisih antara 10°C ke 20°C sama dengan selisih 20°C ke 30°C, yaitu 10°C. - Skor IQ (Intelligence Quotient)
Rentang antar skor bersifat tetap (contoh: selisih IQ 100 ke 110 sama dengan 110 ke 120). - Tanggal dalam kalender (tahun, bulan, hari)
Selisih waktu antara 1 Januari ke 2 Januari sama dengan 10 Januari ke 11 Januari. - Jam dalam format 12 jam atau 24 jam
Perbedaan pukul 08.00 ke 09.00 sama dengan perbedaan 17.00 ke 18.00.
Rumus Interval Kelas
Interval kelas adalah lebar atau jarak antara batas bawah dan batas atas suatu kelas dalam distribusi data berkelompok. Untuk menghitung interval kelas, digunakan rumus :
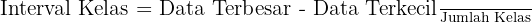
Keterangan:
- Data Terbesar = nilai paling tinggi dalam data.
- Data Terkecil = nilai paling rendah dalam data.
- Jumlah Kelas = banyaknya kelompok kelas yang ingin dibuat.
Kelas interval adalah kelompok nilai yang dibentuk berdasarkan rentang tertentu untuk mengelompokkan data mentah menjadi lebih teratur. Dengan adanya kelas interval, proses penyusunan tabel distribusi frekuensi menjadi lebih sistematis karena setiap data ditempatkan ke dalam kelompok sesuai batas bawah dan batas atas yang telah ditentukan. Konsep ini membantu memudahkan analisis, terutama ketika data jumlahnya besar dan perlu diringkas dalam bentuk yang lebih mudah dibaca. Rumus kelas interval digunakan untuk menentukan rentang atau lebar setiap kelompok data dalam distribusi frekuensi. Rumus kelas interval pada dasarnya sama dengan interval kelas, yaitu membagi selisih antara data terbesar dan data terkecil dengan jumlah kelas yang akan dibentuk. Dengan menggunakan rumus kelas interval, setiap kelas memiliki ukuran yang konsisten sehingga memudahkan proses pengelompokan data dan analisis statistik selanjutnya.

Rumus Sturges
Dalam menentukan jumlah kelas yang ideal pada suatu tabel distribusi frekuensi, salah satu metode yang paling banyak digunakan adalah rumus Sturges. Rumus ini membantu peneliti memperoleh jumlah kelas yang proporsional berdasarkan banyaknya data sehingga distribusi menjadi lebih rapi dan mudah dianalisis. Rumus Sturges dituliskan sebagai berikut:
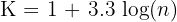
Keterangan:
- K = jumlah kelas yang disarankan
- n = jumlah seluruh data
Dengan menggunakan rumus Sturges, jumlah kelas yang terbentuk biasanya lebih stabil dan tidak terlalu banyak atau terlalu sedikit, sehingga proses penghitungan seperti interval kelas menjadi lebih akurat dan terstruktur.
Cara Mencari Interval Kelas
Setelah jumlah kelas ditentukan menggunakan rumus Sturges, langkah berikutnya adalah menghitung interval kelas. Cara menentukan interval kelas dilakukan dengan membagi rentang data terhadap jumlah kelas yang telah diperoleh. Rentang data dihitung dari selisih antara data terbesar dan data terkecil. Rumusnya adalah:
Interval Kelas=Data Terbesar−Data TerkecilK\text{Interval Kelas} = \frac{\text{Data Terbesar} - \text{Data Terkecil}}{K}Interval Kelas=KData Terbesar−Data Terkecil Dengan cara ini, setiap kelas akan memiliki lebar yang sama sehingga memudahkan penyusunan tabel distribusi frekuensi dan analisis data secara keseluruhan.
Interval Statistik
Interval statistik adalah rentang nilai yang digunakan dalam analisis data untuk mengelompokkan informasi mentah menjadi bagian-bagian yang lebih mudah dibaca dan diinterpretasikan. Dengan membagi data ke dalam interval tertentu, seorang analis dapat melihat pola, kecenderungan, serta variasi yang muncul dalam sebaran data. Interval ini menjadi elemen penting dalam berbagai metode statistik, terutama ketika data berjumlah besar dan perlu diringkas secara efisien. Dalam konteks distribusi frekuensi, interval statistik berfungsi sebagai dasar pembentukan kelas-kelas data. Setiap interval memiliki batas bawah dan batas atas yang menentukan posisi data dalam kelompok tertentu. Penggunaan interval statistik mempermudah pembuatan tabel, grafik, maupun analisis lanjutan, karena data yang awalnya acak dapat disusun menjadi struktur yang lebih teratur dan informatif.
Garis Interval dalam Matematika
Garis interval matematika adalah representasi grafis dari interval pada garis bilangan. Garis interval membantu memvisualisasikan rentang angka yang termasuk dalam interval. Berikut adalah beberapa contoh garis interval:
- Untuk interval tertutup [2, 5], gambar garis interval mencakup semua titik antara 2 dan 5, termasuk titik 2 dan 5.
- Untuk interval terbuka (2, 5), gambar garis interval mencakup semua titik antara 2 dan 5, tetapi tidak termasuk titik 2 dan 5.
- Untuk interval setengah terbuka [2, 5), gambar garis interval mencakup semua titik antara 2 dan 5, termasuk titik 2 tetapi tidak termasuk titik 5.
Periksa di sini untuk les online matematika
Interval Waktu dalam Matematika
Interval waktu adalah konsep lain dari interval yang sering digunakan dalam konteks fisika dan ilmu lainnya. Interval waktu merujuk pada jarak waktu antara dua kejadian. Misalnya, interval waktu antara jam 2 siang dan 4 sore adalah 2 jam.
Dalam fisika, interval waktu sangat penting dalam perhitungan kecepatan, percepatan, dan gerak benda. Misalnya, rumus kecepatan rata-rata adalah:
\[ v = \frac{d}{t} \]
Di mana \( d \) adalah jarak yang ditempuh dan \( t \) adalah interval waktu yang diperlukan untuk menempuh jarak tersebut.
Untuk memahami penerapan konsep ini secara lebih konkret, kita dapat melihat berbagai contoh interval yang sering digunakan dalam kehidupan sehari-hari maupun dalam analisis matematika. Misalnya, interval suhu antara 20°C hingga 30°C, interval waktu dari pukul 08.00 hingga 10.00, atau interval nilai ujian yang dikelompokkan dari 70–79. Contoh-contoh tersebut menunjukkan bagaimana interval mempermudah kita mengelompokkan, membaca, dan menafsirkan data dalam bentuk rentang tertentu sehingga informasi dapat dipahami secara lebih terstruktur.
Cek di sini jika sedang mencari les matematika sidoarjo
Cek di sini jika sedang mencari guru les matematika terdekat
Contoh Soal Interval dalam Matematika
Interval dalam matematika merupakan konsep yang sangat penting, terutama dalam konteks analisis dan penyelesaian masalah yang melibatkan rentang bilangan. Memahami contoh soal interval dapat membantu memperdalam pemahaman mengenai cara kerja interval dan aplikasinya. Berikut ini beberapa contoh soal interval dalam matematika yang diikuti oleh penyelesaiannya.
Cari tahu cara memperluas tanda kurung dalam aljabar.
Contoh Soal 1: Interval Terbuka
Soal:
Tentukan himpunan bilangan real yang memenuhi 3 < x < 7.
Penyelesaian:
Untuk menentukan interval yang sesuai, kita perhatikan bahwa bilangan real yang memenuhi persamaan tersebut adalah semua bilangan yang lebih besar dari 3 dan lebih kecil dari 7.
Interval ini dapat ditulis dalam notasi interval sebagai (3, 7).
Garis Bilangan:
- Gambar garis bilangan dengan dua titik pada angka 3 dan 7.
- Buat lingkaran kosong pada angka 3 dan 7 untuk menunjukkan bahwa angka 3 dan 7 tidak termasuk dalam interval.
- Tarik garis yang menghubungkan kedua lingkaran kosong tersebut untuk menunjukkan semua bilangan di antara 3 dan 7.
Contoh Soal 2: Interval Tertutup
Soal:
Tentukan himpunan bilangan real yang memenuhi 1 ≤ x ≤ 5.
Penyelesaian:
Bilangan real yang memenuhi persamaan ini adalah semua bilangan yang lebih besar atau sama dengan 1 dan lebih kecil atau sama dengan 5.
Interval ini dapat ditulis dalam notasi interval sebagai [1, 5].
Garis Bilangan:
- Gambar garis bilangan dengan dua titik pada angka 1 dan 5.
- Buat lingkaran penuh pada angka 1 dan 5 untuk menunjukkan bahwa kedua angka ini termasuk dalam interval.
- Tarik garis yang menghubungkan kedua lingkaran penuh tersebut untuk menunjukkan semua bilangan di antara 1 dan 5.
Contoh Soal 3: Interval Setengah Terbuka (Kiri Terbuka, Kanan Tertutup)
Soal:
Tentukan himpunan bilangan real yang memenuhi 2 < x ≤ 6.
Penyelesaian:
Bilangan real yang memenuhi persamaan ini adalah semua bilangan yang lebih besar dari 2 dan lebih kecil atau sama dengan 6.
Interval ini dapat ditulis dalam notasi interval sebagai (2, 6].
Garis Bilangan:
- Gambar garis bilangan dengan dua titik pada angka 2 dan 6.
- Buat lingkaran kosong pada angka 2 dan lingkaran penuh pada angka 6 untuk menunjukkan bahwa angka 2 tidak termasuk dalam interval, sedangkan angka 6 termasuk dalam interval.
- Tarik garis yang menghubungkan lingkaran kosong dan lingkaran penuh tersebut untuk menunjukkan semua bilangan di antara 2 dan 6.
Contoh Soal 4: Interval Setengah Terbuka (Kiri Tertutup, Kanan Terbuka)
Soal:
Tentukan himpunan bilangan real yang memenuhi -4 ≤ x < 3.
Penyelesaian:
Bilangan real yang memenuhi persamaan ini adalah semua bilangan yang lebih besar atau sama dengan -4 dan lebih kecil dari 3.
Interval ini dapat ditulis dalam notasi interval sebagai [-4, 3).
Garis Bilangan:
- Gambar garis bilangan dengan dua titik pada angka -4 dan 3.
- Buat lingkaran penuh pada angka -4 dan lingkaran kosong pada angka 3 untuk menunjukkan bahwa angka -4 termasuk dalam interval, sedangkan angka 3 tidak termasuk dalam interval.
- Tarik garis yang menghubungkan lingkaran penuh dan lingkaran kosong tersebut untuk menunjukkan semua bilangan di antara -4 dan 3.
Contoh Soal 5: Interval Tak Terbatas (Negatif)
Soal:
Tentukan himpunan bilangan real yang memenuhi x ≤ -2.
Penyelesaian:
Bilangan real yang memenuhi persamaan ini adalah semua bilangan yang lebih kecil atau sama dengan -2.
Interval ini dapat ditulis dalam notasi interval sebagai (-∞, -2].
Garis Bilangan:
- Gambar garis bilangan dengan titik pada angka -2.
- Buat lingkaran penuh pada angka -2 untuk menunjukkan bahwa angka -2 termasuk dalam interval.
- Tarik garis ke arah kiri tanpa batas (menuju negatif tak terhingga) untuk menunjukkan semua bilangan yang lebih kecil atau sama dengan -2.
Cari tahu cara membuat kerucut menggunakan geometri.
Interaksi antara Interval
Irisan antara interval [a ; b] dan [c ; d] adalah himpunan bilangan real x yang berada di [a ; b] dan [c ; d]. Ini dilambangkan dengan ∩.
Temukan berbagai guru Matematika SMP di Superprof.

Pelajari tentang ubin dan pengubinan.
Bayangkan a, b, c, dan d adalah empat bilangan bulat positif dengan irisan I:
I=[a ; b] ∩ [c ; d] ou I=[c ; d] ∩ [a ; b]
Misalnya:
2 ∈[0 ; 5] ∩[2 ; 6] car 2 ∈[0 ; 5] et 2 [2 ; 6]
Untuk menentukan irisan antara dua himpunan, ada baiknya mewakilinya sebagai himpunan keduanya sendiri. Anda akan tahu cara mengerjakan ini.
Gabungan Himpunan Interval
Ini adalah bilangan real di interval [a ; b] dan [c ; d].
Gabungan disimbolkan dengan ∪.
Ini dapat ditulis sebagai:
U=[a ; b] ∪ [c ; d] atau U=[c ; d] ∪ [a ; b]
Misalnya:
2 ∈[0 ; 5] ∪ [2 ; 6] karena 2 ∈[0 ; 5]
3,8 ∈[0 ; 5] ∪ [2 ; 6] karena 3,8 ∈[0 ; 6]
Untuk menentukan irisan dua himpunan interval, Anda bisa memplotnya pada garis bilangan.
Pelajari cara menghitung hasil bagi.
Pertidaksamaan (Inequation)
Anda perlu ingat bahwa solusi dari pertidaksamaan selalu merupakan interval atau himpunan kosong.
Ini menggunakan x yang tidak diketahui sebagai:
A (x) ≤ B(x) atau A(x)<B(x) di mana x adalah variabel yang tidak diketahui.
Untuk menyelesaikan pertidaksamaan ini, Anda perlu menemukan semua nilai untuk x yang memenuhi pertidaksamaan: himpunan bilangan real untuk x adalah solusinya.
Berikut adalah kemungkinan transformasi untuk pertidaksamaan ke ekuivalen.
- Menambah atau mengurangi bilangan yang sama ke atau dari kedua anggota.
- Mengalikan atau membagi kedua anggota dengan bilangan positif yang sama.
- Mengalikan atau membagi kedua anggota dengan bilangan negatif yang sama.
- Memperluas, memfaktorkan, atau mengurangi anggota.
Lihat artikel kami tentang konjektur matematika.
Pertaksamaan (Inequalities)
Ada tiga aturan pertaksamaan. Pertama, Anda selalu bisa menambahkan angka yang sama ke tiap anggota pertaksamaan: jika a≤b, maka a+c≤b+c.
Kedua adalah Anda bisa menjadi anggota bersama: jika a≤b dan c≤d, maka a+c≤b+d.
Aturan ketiga adalah Anda bisa mengalikan atau membagi setiap pertidaksamaan dengan angka yang sama.
Cek di sini untuk les matematika SMA terdekat
Nilai Mutlak
Nilai mutlak berada di tengah interval pada garis bilangan.
Ingatlah jarak antara a dan b.
Semoga ini cukup untuk membuat Anda memulai dengan interval. Seperti yang telah Anda pahami, dalam matematika, bilangan real beralih dari -∞ ke +∞. Sebagian besar waktu, kita semua tertarik pada himpunan bilangan ini. Himpunan interval sama bergunanya untuk menemukan bilangan yang ada di dalamnya seperti menemukan bilangan yang dikecualikan.
Jika Anda ingin mempelajari lebih lanjut tentang matematika, pertimbangkan mendapatkan bantuan dari salah satu guru berbakat dan berpengalaman di website Superprof.
Anda bisa menemukan guru yang ahli dalam matematika untuk semua level mulai dari sekolah menengah hingga universitas. Ada berbagai cara untuk belajar dari guru privat jadi pastikan Anda memilih jenis bimbingan yang cocok untuk Anda, bagaimana Anda ingin belajar, dan anggaran Anda.
Bimbingan tatap muka adalah yang paling umum dan biasanya melibatkan guru yang hanya mengajar satu murid di rumah mereka. Karena hanya ada satu murid, guru dapat menyesuaikan setiap menit pelajaran untuk mereka dan memastikan mereka mendapatkan hasil maksimal dari setiap menit yang mereka pelajari bersama. Tentu saja, layanan yang dipesan terlebih dahulu ini lebih mahal karena Anda membayar untuk bimbingan tersebut serta waktu yang dihabiskan guru untuk merencanakan kursus dan perjalanan ke rumah murid.
Bimbingan online juga dapat diajarkan satu lawan satu, tapi karena guru tidak perlu pergi ke tempat murid dan dapat mengajarkan lebih banyak pelajaran setiap pekan, mereka cenderung tidak terlalu mahal. Meskipun ini tidak ideal untuk subjek dan keterampilan langsung, bimbingan online bagus untuk subjek-subjek akademis seperti matematika.
Bimbingan kelompok adalah pilihan bagus untuk mereka yang memiliki anggaran terbatas. Dengan beberapa murid menghadiri kelas yang sama, guru mampu membebankan biaya yang lebih sedikit untuk setiap murid. Meskipun Anda tidak akan menikmati les yang disesuaikan hanya untuk Anda, Anda bisa menikmati membayar lebih sedikit untuk mereka. Jika Anda dan beberapa teman, anggota keluarga, teman sekelas, atau kolega perlu belajar lebih lanjut tentang matematika, bimbingan kelompok bisa menjadi opsi yang sangat bagus dan terjangkau.
Kesimpulan
Dalam analisis data berkelompok, memahami konsep interval dan pembentukan kelas menjadi langkah penting untuk menyajikan data secara lebih terstruktur. Proses ini melibatkan beberapa tahapan, mulai dari mengetahui cara menghitung interval kelas, yaitu dengan membagi selisih antara data terbesar dan data terkecil dengan jumlah kelas yang diperlukan. Selain itu, pemahaman tentang cara menentukan kelas interval juga sangat penting agar setiap kelompok data memiliki batas yang jelas dan konsisten, sehingga penyusunan tabel distribusi frekuensi menjadi lebih akurat. Dengan menerapkan konsep-konsep tersebut—mulai dari skala interval, rumus Sturges, hingga perhitungan interval—peneliti atau pelajar dapat menganalisis data secara lebih efektif. Struktur yang rapi memudahkan identifikasi pola, tren, serta penyimpangan dalam data, menjadikan hasil analisis lebih informatif dan mudah dipahami dalam konteks statistik maupun penelitian akademik.
Jangan lupa bahwa banyak dari guru di Superprof menawarkan jam bimbingan pertama secara gratis sehingga Anda bisa mencoba beberapa bimbingan sebelum memutuskan mana yang tepat untuk Anda. Anda juga bisa mencoba berbagai jenis bimbingan jika Anda tidak yakin mana yang lebih Anda sukai.
Menggaris bawahi persyaratan Anda sebelum mencari guru selalu menjadi ide yang bagus, Anda bisa melihat pengalaman apa yang mereka miliki, apa yang dikatakan siswa lainnya tentang mereka, dan berapa biaya yang mereka kenakan setiap jam. Sebelum Anda mulai menghubungi guru dan mengatur les gratis, kami sarankan Anda mempersempit pencarian guru yang memenuhi persyaratan Anda.
Tahukah Anda bahwa Anda bisa menemukan guru matematika yang piawai di sini?
Ringkaskan dengan AI















