Saat Anda berada di kelas 11, materi matematika apa yang paling Anda sukai? Tentu saja yang tidak bisa Anda lewatkan adalah materi kalkulus, mulai dari turunan juga integral. Bagi sebagian besar siswa, kalkulus dapat dikategorikan sebagai salah satu materi yang sulit dipahami karena dalam kehidupan nyata jarang terjadi stagnasi.
Pada integral kelas 11, salah satu jenis integral yang akan dipelajari adalah integral tak tentu. Apa itu integral tak tentu? Dan apa saja sifat integral tak tentu? Mari kita pelajari bersama!
Di artikel kali ini, kita akan berfokus membahas tentang pengertian integral tak tentu, rumus integral tak tentu, beserta sifat sifat integral tak tentu. Jika Anda merasa kesulitan dalam memahami materi matematika, jangan ragu untuk meminta bantuan pada kursus privat Superprof!
Periksa di sini jika ingin mengetahui apa itu simpangan baku

Pengertian Integral Tak Tentu
Setiap bentuk operasi matematis pasti memiliki operasi kebalikan atau invers, seperti penjumlahan dan pengurangan, perkalian dan pembagian, akar dan pangkat. Kebalikan itu juga berlaku pada turunan, di mana kebalikan dari turunan adalah integral. Integral merupakan anti turunan atau kebalikan dari turunan yang berfungsi untuk menentukan daerah, volume, titik pusat, dan lainnya.
Saat belajar turunan, pasti kamu akan mendapatkan penulisan suatu fungsi disertai tanda petik, seperti f’(x), bukan? Arti f’(x) adalah turunan dari fungsi f(x). Lantas, bagaimana cara mendapatkan f(x) jika yang diketahui f’(x)? Nah, f(x) sendiri bisa diketahui dengan cara mengintegralkan fungsi f’(x) terhadap dx. Jika kita memiliki fungsi f(x) lalu mengoperasikan turunan terhadapnya, hasilnya adalah f’(x). Namun, jika kita ingin membalikkan fungsi f’(x) ke fungsi asalnya yaitu f(x), maka kita perlu mengoperasikan integral terhadapnya. Perhatikan contoh di bawah ini!
Turunan;
df(x)/dx = f’(x)
Sekarang kita balik, dengan dikalikan silang maka menjadi:
df(x) = f’(x)dx
Selanjutnya ditambahkan lambang integral (∫), menjadi :
∫df(x) = ∫f’(x)dx
∫f’(x)dx = f(x)+C
Maka dapat disimpulkan bahwa; Integral tak tentu (indefinite integral) adalah integral yang tidak memiliki batas batas nilai tertentu, sehingga hanya diperoleh fungsi umumnya saja disertai suatu konstanta C. Atau juga dapat diartikan, integral tak tentu merupakan suatu fungsi baru yang punya turunan dari fungsi aslinya dan fungsi tersebut belum memiliki nilai pasti. Itulah mengapa dalam integral tak tentu ada yang namanya konstanta (C).
Persamaan Dasar Integral Tak Tentu
Persamaan dasar integral tak tentu merupakan konsep utama dalam materi integral matematika yang digunakan untuk mencari bentuk fungsi asal dari suatu turunan. Dengan kata lain, integral (atau yang sering disebut juga dengan antiderivatif, yang merupakan sinonim integral) adalah kebalikan dari operasi diferensial. Dalam praktiknya, integral tak tentu sering digunakan untuk mempelajari fungsi integral, cara integral, serta penerapan kalkulus integral dalam berbagai soal dan contoh integral.
Menurut integral adalah KBBI (Kamus Besar Bahasa Indonesia), integral merujuk pada operasi matematika untuk menghitung total atau jumlah suatu fungsi dalam interval tertentu, baik itu dalam bentuk integral tak tentu maupun integral tentu. Dalam proses cara menghitung integral, pangkat pada variabel akan mengalami perubahan. Jika suatu fungsi awalnya memiliki pangkat tertentu, maka setelah diintegralkan pangkat tersebut akan bertambah satu. Proses ini selalu menghasilkan konstanta tambahan, yang disebut konstanta integrasi. Rumus dasar integral juga selalu menyertakan konstanta ini karena hasil integral tidak bersifat tunggal.
Konstanta integrasi muncul karena sebuah fungsi dapat memiliki banyak bentuk asal yang berbeda, namun tetap menghasilkan turunan yang sama. Konsep ini menjadi pondasi penting sebelum mempelajari intergral tentu dan rumus integral tentu yang digunakan untuk menghitung luas daerah atau besaran tertentu.
Agar Anda dapat lebih memahami pengertian integral tak tentu, mari simak rumus umum integral tak tentu berikut ini!
Cek di sini untuk mengetahui statistika deskriptif
Rumus Integral Tak Tentu
Sekarang Anda sudah memahami apa itu integral tak tentu dan hubungannya dengan turunan. Kini, saatnya Anda memahami rumus integral tak tentu. Rumus umum integral tak tentu, sebagai berikut;
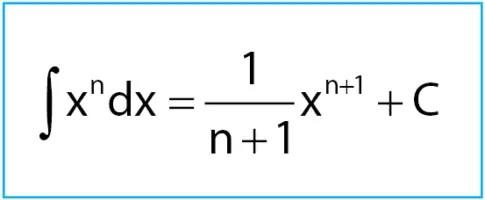
Agar lebih memahaminya, mari kita coba praktikan ke dalam contoh soal berikut ini.
Soal:
Jika f(x)=x^4, maka integral f(x) terhadap dx adalah….
Jawab:
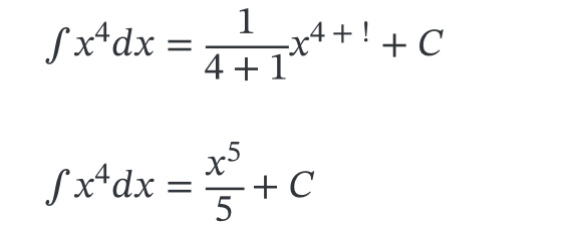
Nah, sekarang sudah jelas ya cara menghitung integral tak tentu dari suatu fungsi. Anda hanya perlu memasukkan angka-angka pada fungsi ke dalam rumus umum di atas. Akan tetapi, yang menjadi pertanyaan adalah dari mana datangnya huruf C pada hasil pengintegralan tak tentu?
Jawabannya, integral tak tentu tidak memiliki batas atas dan bawah sehingga konstanta yang terdapat pada hasil pengintegralannya belum jelas nilainya.
Sebagai contoh, jika kita turunkan fungsi f(x)=x³, akan diperoleh nilai f’(x)=3x². Jika kita turunkan fungsi f(x)=x³+10, akan diperoleh hasil yang sama yaitu f’(x)=3x². Begitu juga kalau kita turunkan f(x)=x³+15, hasilnya sama yaitu f’(x)=3x².
Dengan demikian, kebalikan atau integral tak tentu dari fungsi f’(x)=3x² , memiliki banyak kemungkinan yang belum pasti nilainya, bisa x³, x³+10, atau x³+15. Itulah mengapa pada rumus umum integral tak tentu disertai dengan huruf C yang berarti konstanta.
Cobalah untuk menguji pemahaman Anda dengan mengerjakan beberapa latihan soal terkait integral tak tentu. Latihan soal dapat meningkatkan pemahaman Anda tentang matematika.
Cek di sini untuk mengetahui cara menentukan diskriminan pada persamaan kuadrat

Sifat Sifat Integral Tak Tentu
Sifat integral tak tentu adalah bentuk lain dari operasi integral sedemikian sehingga bisa memudahkan Anda dalam menyelesaikan permasalahan terkait integral. Adapun sifat-sifat integral tak tentu adalah sebagai berikut.
Pangkat
Sifat pertama ini sama halnya dengan rumus umum pada integral tak tentu.
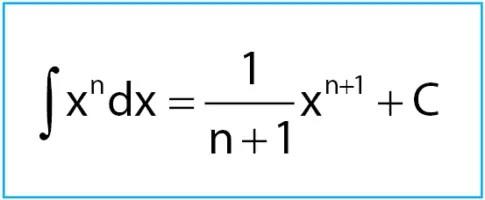
Konstanta
Sifat kedua berkaitan dengan integral suatu fungsi yang memuat suatu konstanta seperti:
∫k.f(x)dx=k∫f(x)dx
Jika Anda menjumpai bentuk seperti di atas, keluarkan saja konstanta k dari tanda integral, sehingga Anda bisa fokus menyelesaikan integral fungsinya.
Permasalahan Dapat Diselesaikan dengan Integral Tak Tentu
Soal integral tak tentu bukan sekadar simbol matematika. Dalam praktik, konsep ini digunakan untuk menyelesaikan berbagai masalah, mulai dari aplikasi integral dalam fisika hingga teknik. Beberapa kasus yang umum dihadapi antara lain:
Menentukan Persamaan Kurva dari Gradien yang Diketahui
Gradien merupakan turunan pertama dari suatu fungsi kurva. Jika persamaan gradien sudah diketahui, bentuk kurvanya bisa dicari dengan cara integral. Hal ini merupakan contoh nyata penggunaan kalkulus integral dalam menentukan fungsi dari turunan integral.
Menentukan Fungsi Kecepatan dan Posisi
Dalam pelajaran fisika, konsep posisi, kecepatan, dan percepatan saling berkaitan. Kecepatan merupakan turunan dari posisi, sedangkan percepatan adalah turunan dari kecepatan. Dengan cara integral, fungsi kecepatan dapat ditentukan dari fungsi percepatan, dan begitu pula fungsi posisi. Contoh penerapan ini sering muncul dalam aplikasi integral sehari-hari.
Cek di sini jika sedang mencari tempat les matematika
Penjumlahan dan pengurangan
Sifat ketiga berlaku untuk penjumlahan dua fungsi di dalam integral seperti berikut.
∫[f(x)±g(x)]dx=∫f(x)dx±g(x)dx
Dua fungsi yang dijumlahkan dalam satu tanda integral bisa Anda ubah menjadi penjumlahan integral masing-masing fungsinya. Sifat ini bisa memudahkan Anda dalam menyelesaikan fungsi-fungsi yang cukup panjang. Hal ini juga berlaku untuk pengurangan dua fungsi.
Kesalahan yang Sering Terjadi dalam Integral Tak Tentu
Meskipun cara integral tak tentu terlihat sederhana, masih banyak siswa yang melakukan kesalahan saat mengerjakan soal. Kesalahan ini umumnya terjadi karena kurangnya pemahaman konsep dasar, bukan karena rumus yang terlalu sulit.
Salah satu kesalahan yang sering muncul adalah lupa menambahkan konstanta integrasi (C) pada hasil akhir. Padahal, konstanta ini sangat penting karena menunjukkan bahwa hasil integral tidak bersifat tunggal. Tanpa konstanta integrasi, jawaban dianggap belum lengkap.
Kesalahan lain adalah salah mengubah pangkat variabel. Pada integral tak tentu, pangkat variabel harus ditambah satu terlebih dahulu sebelum dibagi dengan pangkat barunya. Banyak siswa yang langsung membagi tanpa menyesuaikan pangkat, sehingga hasilnya keliru.
Selain itu, ada juga yang keliru mengintegralkan konstanta. Konstanta sering dianggap hilang, padahal integral dari konstanta tetap menghasilkan fungsi linear. Ketidaktelitian dalam membaca bentuk fungsi juga sering menyebabkan kesalahan perhitungan.
Dengan memahami kesalahan umum, proses cara menghitung integral menjadi lebih akurat, baik untuk soal integral tak tentu maupun conto integral lainnya.
Contoh Soal Cerita Integral Tak Tentu (Versi Naratif)
Soal Cerita 1
Menentukan Fungsi dari Laju Perubahan Tetap
Seorang peneliti mengamati sebuah proses sederhana di laboratorium. Ia menemukan bahwa laju perubahan suatu besaran selalu bernilai tetap dan dinyatakan dengan angka 4. Peneliti tersebut ingin mengetahui bentuk fungsi dari besaran tersebut terhadap variabel (x).
Tentukan fungsi yang dimaksud. Bentuk fungsi besaran tersebut terhadap x dapat dicari dengan rumus dasar integral:
Pembahasan:
Karena laju perubahan besaran tersebut bersifat konstan, maka untuk mencari fungsi asalnya diperlukan proses integral terhadap nilai tersebut.
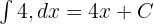
Konstanta integrasi (C) menyatakan nilai awal besaran sebelum pengamatan dilakukan.
Soal Cerita 2
Menentukan Fungsi Posisi dari Gradien Kurva
Sebuah kurva pada bidang koordinat memiliki gradien yang berubah sesuai dengan nilai (x). Gradien kurva tersebut dinyatakan oleh fungsi (x^2). Untuk mengetahui persamaan kurva tersebut, gradien yang diketahui perlu diolah lebih lanjut.
Tentukan persamaan fungsi kurva tersebut. Fungsi posisi diperoleh dengan integral tak tentu:
Pembahasan:
Karena gradien merupakan turunan pertama dari fungsi kurva, maka untuk memperoleh fungsi kurva, gradien harus diintegralkan.
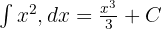
Konstanta (C) menunjukkan bahwa terdapat banyak kurva berbeda yang memiliki gradien yang sama.
Soal Cerita 3
Menentukan Fungsi Kecepatan dari Laju Perubahan Kecepatan
Sebuah benda bergerak lurus dengan laju perubahan kecepatan yang bergantung pada nilai (x). Laju perubahan tersebut dinyatakan oleh fungsi (6x^2). Untuk mengetahui bagaimana kecepatan benda berubah, fungsi tersebut perlu diintegralkan.
Tentukan fungsi kecepatan benda tersebut.
Pembahasan:
Laju perubahan kecepatan merupakan turunan dari kecepatan. Oleh karena itu, untuk mendapatkan fungsi kecepatan, laju perubahan tersebut harus diintegralkan.
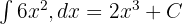
Konstanta integrasi (C) menyatakan kecepatan awal benda.
Soal Cerita 4
Menentukan Fungsi dari Perubahan yang Berbentuk Kuadrat
Sebuah fenomena alam diamati dan diketahui bahwa laju perubahannya mengikuti bentuk kuadrat dari suatu fungsi, yaitu ((x + 2)^2). Untuk memahami fenomena tersebut secara lebih mendalam, diperlukan fungsi asal dari laju perubahan tersebut.
Tentukan fungsi yang dimaksud.
Pembahasan:
Untuk mendapatkan fungsi asal, laju perubahan yang diketahui harus diintegralkan terlebih dahulu.
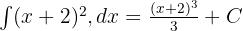
Konstanta (C) menunjukkan nilai awal fungsi sebelum perubahan terjadi.
Soal Cerita 5
Menentukan Fungsi dari Gabungan Beberapa Laju Perubahan
Seorang ahli mencatat bahwa laju perubahan suatu besaran dipengaruhi oleh beberapa komponen, yaitu komponen kuadrat, linear, dan konstanta. Laju perubahan tersebut dinyatakan dengan fungsi
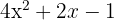
Untuk mengetahui fungsi asal dari besaran tersebut, lakukan perhitungan yang sesuai.
Pembahasan:
Karena fungsi yang diintegralkan terdiri dari beberapa suku, maka proses integrasi dilakukan dengan mengintegralkan setiap suku secara terpisah.
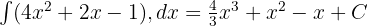
Konstanta integrasi (C) menyatakan nilai awal fungsi yang dicari.
Contoh-contoh di atas adalah contoh soal integral tak tentu yang sering muncul dalam integral matematika dan memerlukan pemahaman rumus rumus integral.
Integral Cos dan Variasi Fungsi Integral
Selain fungsi polinomial, cara integral juga diterapkan pada fungsi trigonometri, seperti integral cos. Rumusnya:
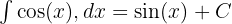
Fungsi ini sering digunakan dalam aplikasi integral, terutama dalam fisika, elektronika, dan perhitungan gelombang. Dengan memahami rumus dasar integral, cara integral menjadi lebih fleksibel untuk berbagai tipe fungsi.
Untuk menguji kemampuan Anda dalam materi integral tak tentu, cobalah kerjakan beberapa latihan soal berikut ini dan Anda bisa diskusikan bersama guru Anda.
- ʃ 4 dx
- ʃ x^2 dx
- ʃ 6x^2 dx
- ʃ (x + 2)^2 dx
- ʃ (4x2+ 2x - 1) dx
Tapi bagaimana jika fungsinya bukanlah fungsi aljabar sederhana seperti contoh di atas? Bagaimana rumus dasar untuk integral tak tentu fungsi trigonometri? Bagi Anda yang kesulitan dalam memahami materi matematika, terlebih kalkulus, maka guru privat Superprof adalah solusi terbaik untuk mendukung kemajuan Anda. Guru privat akan membimbing Anda secara penuh dan menjadikan proses belajar menjadi lebih menyenangkan.
Periksa di sini untuk mengetahui cara mencari rata rata data kelompok
Ringkaskan dengan AI
















