Belajar merupakan salah satu kebutuhan manusia . Tanpa disadari, masa kecil kita dimulai dengan belajar. Banyak sekali ilmu yang dapat kita pelajari dengan cara yang menyenangkan dan itu menuai beragam manfaat hingga kita dewasa. Begitupun dengan matematika, materi integral adalah salah satu konsep penting dalam matematika yang memiliki beragam aplikasi di berbagai bidang, termasuk fisika, ekonomi, dan ilmu komputer.
Kini mari kita menjelajahi pengertian integral, rumus dasarnya, dan sifat-sifat integral yang terkait dengan konsep ini. Dengan pemahaman yang baik tentang integral, kita dapat memanfaatkannya secara efektif untuk memecahkan masalah yang melibatkan luas, volume, dan banyak aplikasi matematika lainnya. Mari kita mulai dengan pemahaman dasar tentang materi integral.
Cek di sini untuk kursus matematika terbaik
Integral Adalah…
Secara sederhana, integral adalah konsep matematika yang digunakan untuk mengukur jumlah atau akumulasi suatu variabel dalam interval tertentu. Integral berfungsi untuk menghitung luas di bawah kurva suatu fungsi, atau bisa juga untuk menghitung total perubahan dalam suatu fenomena. Integral adalah kebalikan dari turunan, yang sering dikenal dengan istilah anti-turunan.
Pelajari juga pengertian bilangan rasional untuk menambah pengetahuan Anda!
Rumus Umum Integral
Rumus dasar integral digunakan untuk menghitung luas di bawah kurva atau untuk menghitung total perubahan dalam suatu fungsi. Secara umum, integral dari fungsi f(x) dapat ditulis sebagai:
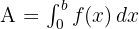
Penjelasan dari rumus ini adalah sebagai berikut:
dan 
: Batas bawah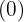 
dan batas atas 
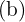dari integral yang menunjukkan panjang interval dari sumbu 
.
A: Luas daerah yang dibatasi oleh fungsi 
dan sumbu x.
: Notasi integral yang menunjukkan operasi integral.
: Fungsi yang akan diintegralkan.
: Menyatakan variabel yang diintegralkan, dalam hal ini adalah x.
Ikuti tulisan Kami lainnya untuk memahami cara pembagian polinomial dalam Matematika!
Jenis-Jenis Integral
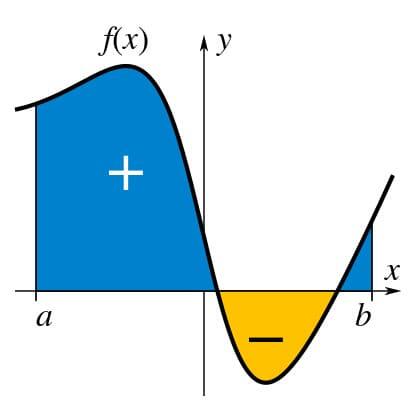
Integral dibagi menjadi dua jenis yaitu integral tentu dan tak tentu. Masing-masing jenis integral memiliki karakteristik yang berbeda. Yuk, kita bahas lebih lanjut.
Integral Tertentu
Integral tertentu adalah jenis integral yang memiliki batas atas dan batas bawah yang jelas. Integral ini menghasilkan nilai numerik dan biasanya digunakan untuk menghitung luas daerah di bawah kurva pada interval tertentu.
Rumus integral tentu adalah:
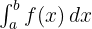
Di sini, a adalah batas bawah dan b adalah batas atas dari interval yang digunakan. Integral ini menghasilkan nilai yang menunjukkan luas area di bawah kurva pada interval [a, b].
Periksa di sini untuk les matematika di Bandung
Sifat-Sifat Integral Tentu
Berikut adalah beberapa sifat sifat integral tentu yang perlu diketahui antara lain:
- Sifat Dasar (Teorema Dasar Kalkulus):
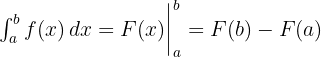
- Sifat Integral Tentu Faktor Konstanta:
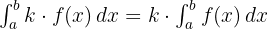
- Aturan Penjumlahan dan Pengurangan:
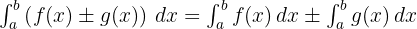
- Sifat Additivitas:
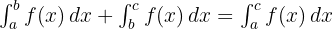
- Pembalikan Batas Integral:
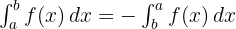
- Integral dengan Batas Sama:
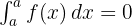
Integral Tak Tentu
Integral tak tentu adalah jenis integral yang tidak memiliki batas atas dan batas bawah, dan hasilnya berupa fungsi, bukan nilai numerik. Biasanya, hasil dari integral tak tentu memuat konstanta integrasi C, karena ada banyak kemungkinan hasil yang dapat dihasilkan dari sebuah fungsi.
Rumus umum untuk integral tak tentu adalah:
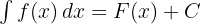
Di mana 
adalah fungsi primitif dari , dan C adalah konstanta integrasi.
Sifat-Sifat Integral Tak Tentu
Berikut adalah sifat-sifat dari integral tak tentu:
- Integral dari
:
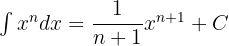
- Integral dengan konstanta:
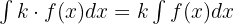
- Integral dari penjumlahan atau pengurangan dua fungsi:
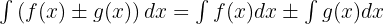
Pahami juga rumus dasar deret dan baris aritmatika di tautan Kami lainnya!
Contoh Soal Integral Dan Pembahasan
Agar lebih paham mengenai integral perlu adanya contoh integral tentu dan tak tentu. Berikut adalah tiga contoh soal integral dan pembahasannya:
Contoh 1: Integral Tentu
Hitunglah integral dari 
pada interval [1, 3]:
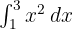
Pembahasan:
Untuk menghitung integral ini, kita akan mengintegralkan 
:
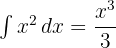
Kemudian kita evaluasi pada batas 1 dan 3:
- 
= 
- 
= 
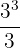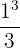
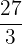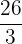
Jadi, hasil integralnya adalah .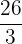
Contoh 2: Integral Tak Tentu
Hitunglah integral dari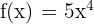 
:
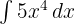
Pembahasan:
Untuk menghitung integral ini, kita gunakan rumus integral untuk :
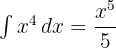
Maka, integral dari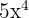 
adalah:
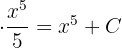
Jadi, hasil integralnya adalah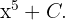 
Contoh 3: Integral Tentu Fungsi Aljabar
Hitunglah integral dari f(x) = 3x + 2 pada interval [0, 4]:
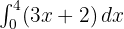
Pembahasan:
Untuk menghitung integral ini, kita integralkan tiap bagian:
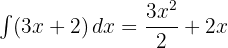
Kemudian kita evaluasi pada batas 0 dan 4:
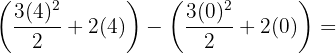
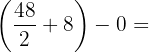
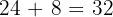
Jadi, hasil integralnya adalah 32.
Latihan Soal
Kerjakan soal latihan berikut:
- Hitunglah integral dari
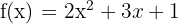pada interval [2, 5] - Hitunglah
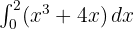
- Tentukan integral dari
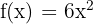pada interval [1, 3] - Hitunglah
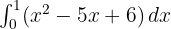
- Tentukan
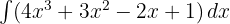
Jika Anda kesulitan memahami materi integral kelas 11, mencari guru privat adalah solusi yang tepat untuk membantu Anda menguasai konsep ini dengan lebih mudah. Dengan bimbingan dari seorang guru privat, Anda dapat mempelajari soal-soal integral secara mendalam, mendapatkan penjelasan yang lebih terperinci, dan latihan yang sesuai dengan kebutuhan Anda. Jangan biarkan kesulitan dalam belajar menghentikan langkah Anda! Temukan guru privat yang tepat di Superprof dan tingkatkan kemampuan Anda dalam matematika hari ini.
Pelajari juga limit fungsi Aljabar!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
