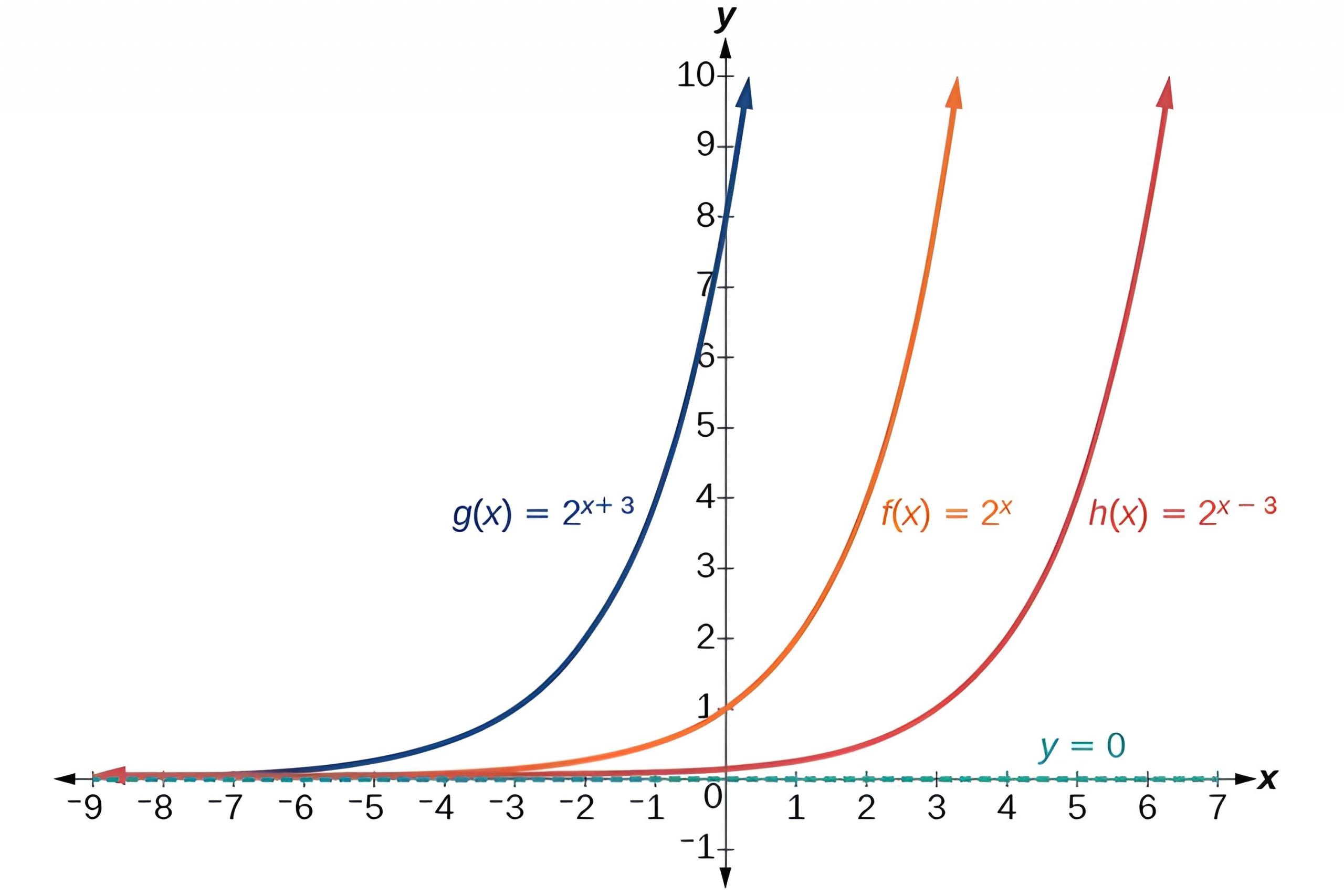
Grafik fungsi eksponensial penting dalam berbagai bidang seperti ekonomi, fisika, dan biologi. Pada artikel kali ini kita akan mendalami ciri-ciri grafik fungsi eksponensial dan memberikan contoh permasalahan yang berkaitan dengannya. Fungsi eksponensial adalah fungsi yang berbentuk f(x) = a^x, dengan "a" adalah konstanta yang disebut basis dan "x" mewakili masukan atau variabel bebas. Grafik fungsi eksponensial memiliki ciri khas yang membedakannya dari jenis fungsi lainnya. Pertama, mari kita bahas bentuk dasar grafik. Ketika basis "a" lebih besar dari 1, grafik akan dimulai dari titik asal (0, 1) dan terus meningkat seiring dengan meningkatnya nilai "x". Sebaliknya, jika basis “a” berada di antara 0 dan 1 tetapi tidak termasuk 0, grafiknya akan mengecil dari kiri ke kanan.
Perilaku ini disebabkan oleh pertumbuhan atau peluruhan eksponensial yang terjadi pada fungsi-fungsi ini. Karakteristik penting lainnya adalah asimtot grafik. Asimtot adalah garis yang didekati grafik tetapi tidak pernah disentuh. Dalam fungsi eksponensial, ketika basis "a" lebih besar dari 1, grafik mendekati sumbu x ketika x mendekati negatif tak terhingga. Sebaliknya, jika basis "a" berada di antara 0 dan 1, grafik mendekati sumbu x ketika x mendekati tak terhingga positif.
Artinya fungsi eksponensial tidak akan pernah berpotongan atau menyentuh sumbu x. Laju pertumbuhan atau penurunan fungsi eksponensial ditentukan oleh nilai basis "a". Ketika "a" lebih besar dari 1, fungsi eksponensial mengalami pertumbuhan eksponensial. Ini berarti bahwa ketika nilai "x" meningkat, nilai f(x) yang bersangkutan juga meningkat dengan laju yang meningkat.
Sebaliknya, jika "a" berada di antara 0 dan 1, fungsi eksponensial mengalami peluruhan eksponensial. Dalam hal ini, ketika nilai "x" meningkat, nilai f(x) yang bersangkutan menurun, tetapi dengan laju yang menurun.
Cek di sini untuk sistem persamaan linear dua variabel dan sistem persamaan linear tiga variabel

Contoh Penggunaan dalam Soal

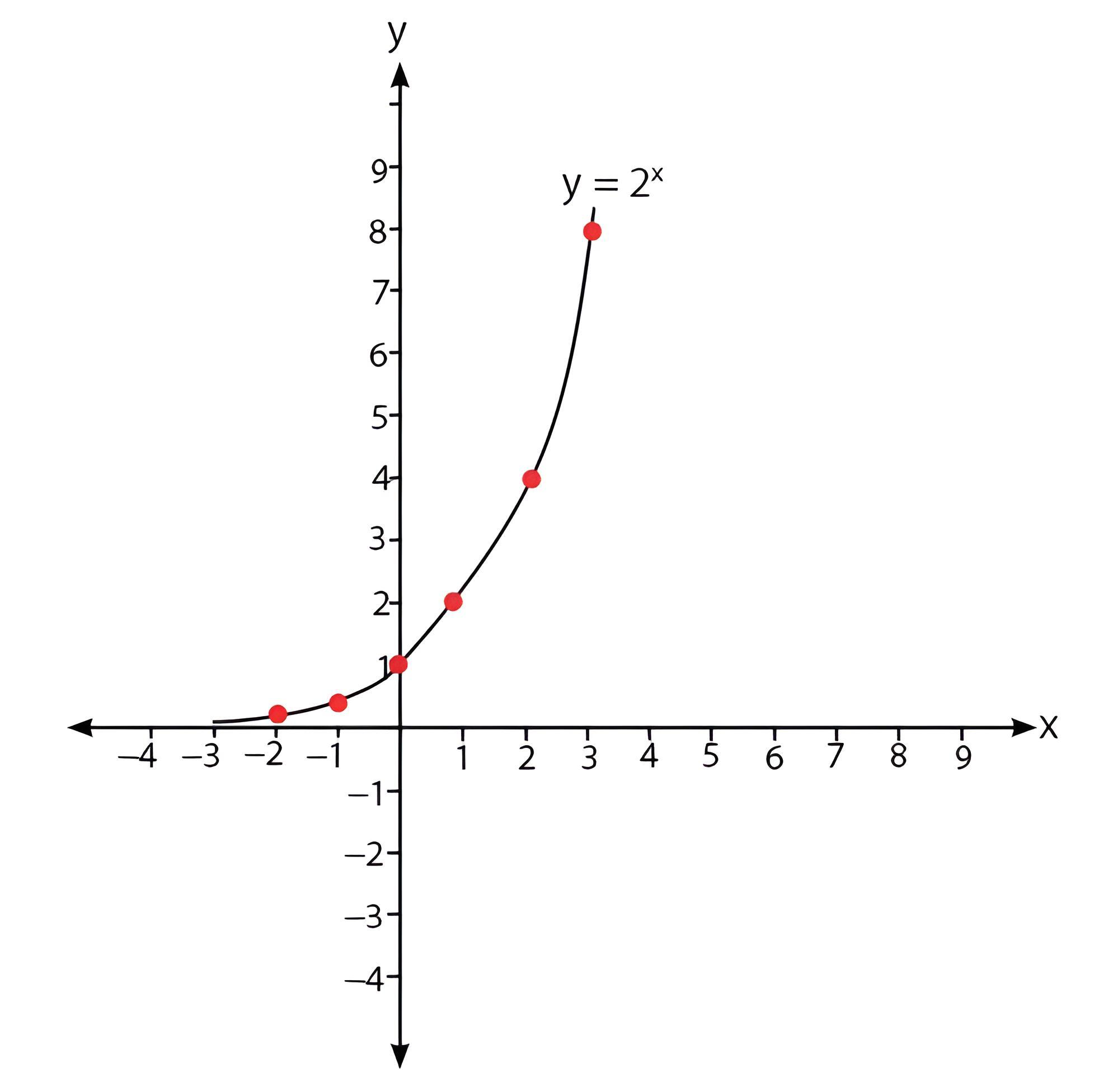
Sekarang mari kita beralih ke beberapa contoh soal yang berkaitan dengan grafik fungsi eksponensial. Contoh-contoh ini akan membantu kita memahami cara menganalisis dan menafsirkan karakteristik fungsi eksponensial. Contoh 1: Diketahui fungsi eksponensial f(x) = 2^x, buat grafik fungsi tersebut dan identifikasi karakteristiknya. Untuk membuat grafik fungsi, kita dapat memplot beberapa titik dengan memilih nilai "x" yang berbeda dan menghitung nilai f(x) yang sesuai. Karena basis "a" adalah 2, kita dapat memulai dengan x = -2, -1, 0, 1, dan 2. f(-2) = 2^(-2) = 1/4 f(-1) = 2^(-1) = 1/2 f(0) = 2^0 = 1 f(1) = 2^1 = 2 f(2) = 2^2 = 4 Dengan memplot titik-titik ini pada sebuah grafik, kita dapat memperhatikan bahwa grafik dimulai pada (0, 1) dan meningkat dengan cepat.
Selain itu, grafik akan mendekati sumbu x ketika x mendekati tak terhingga negatif. Contoh 2: Diketahui fungsi eksponensial f(x) = (1/3)^x, buat grafik fungsi tersebut dan identifikasikan karakteristiknya. Mirip dengan contoh sebelumnya, kita dapat memplot titik dengan memilih nilai "x" yang berbeda dan menentukan nilai f(x) yang sesuai. Karena basis "a" adalah 1/3, kita dapat memilih x = -2, -1, 0, 1, dan 2. f(-2) = (1/3)^(-2) = 9 f(- 1) = (1/3)^(-1) = 3 f(0) = (1/3)^0 = 1 f(1) = (1/3)^1 = 1/3 f(2) = (1/3)^2 = 1/9 Dengan memplot titik-titik ini pada sebuah grafik, kita dapat mengamati bahwa grafik tersebut dimulai pada (0, 1) dan menurun seiring bertambahnya x. Selain itu, grafik mendekati sumbu x ketika x mendekati tak terhingga positif.
Cek di sini untuk mempelajari pertidaksamaan linear dua variabel
Karakteristik utama grafik fungsi eksponen
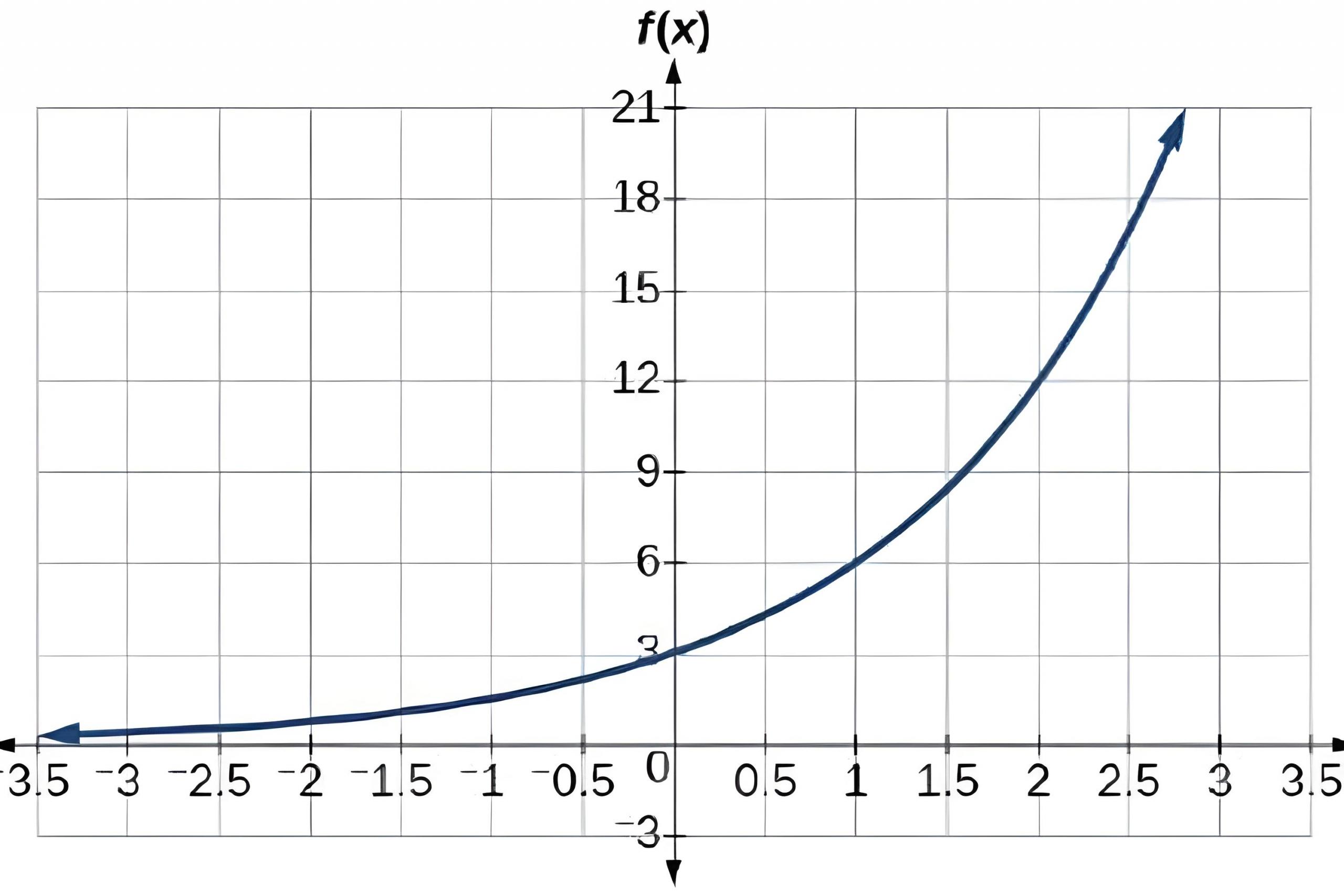
Grafik fungsi eksponen akan selalu berada di sebelah atas sumbu-x dan tidak akan pernah menyentuh atau memotong sumbu-x. Kenapa hal ini terjadi? Karena kita tahu bahwa basis dari fungsi eksponen haruslah bilangan positif, dan jika x mendekati tak-hingga negatif, hasil dari fungsi eksponen akan mendekati nol tanpa pernah mencapainya.
Selain itu, grafik fungsi eksponen cenderung memiliki garis miring ke atas ketika nilai basisnya lebih besar dari 1. Ini mengindikasikan pertumbuhan yang semakin cepat seiring dengan peningkatan nilai x. Sebaliknya, jika basisnya bernilai antara 0 dan 1, grafik akan memiliki garis miring ke bawah, menunjukkan penurunan yang semakin cepat seiring dengan peningkatan nilai x.
Contoh soal yang sering ditemui dalam studi tentang grafik fungsi eksponen adalah mencari nilai asimtot horizontal dan vertikal. Asimtot horizontal adalah garis horizontal yang mendekati grafik fungsi eksponen saat nilai x mendekati tak-hingga positif atau negatif. Asimtot vertikal adalah garis vertikal yang merupakan batas atas atau batas bawah dari grafik fungsi eksponen.
Misalnya, kita memiliki fungsi eksponen y = 3^x. Jika kita memplot grafiknya, kita akan melihat bahwa tidak ada asimtot horizontal, tetapi ada asimtot vertikal di y = 0. Ini berarti bahwa grafik fungsi eksponen akan terus naik seiring dengan peningkatan nilai x tanpa ada batas atas, dan akan terus mendekati tapi tidak akan mencapai nol.
Dalam pelajaran matematika, kita juga sering diberikan contoh soal untuk menggambar grafik fungsi eksponen dan menganalisis sifat-sifatnya. Contoh soal ini biasanya terdiri dari memilih nilai-nilai basis yang tepat, menentukan asimtot, mencari titik perpotongan dengan sumbu-y, dan mengidentifikasi domain dan range dari fungsi eksponen tersebut.
Dalam pembelajaran matematika kelas 10, kita juga akan dibekali dengan pemahaman tentang grafik fungsi eksponensial secara umum. Grafik fungsi eksponensial memiliki kemiripan dengan grafik fungsi eksponen, tetapi memiliki karakteristik yang lebih kompleks. Misalnya, grafik fungsi eksponensial akan memiliki titik perpotongan dengan sumbu-y jika basisnya lebih besar dari 1, sementara jika basisnya antara 0 dan 1, grafiknya tidak akan memotong sumbu-y.
Grafik fungsi eksponen adalah konsep penting dalam matematika yang dapat membantu kita memahami pertumbuhan atau penurunan subur suatu fenomena. Dengan mempelajari dan menganalisis grafik fungsi eksponen, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat dasar fungsi eksponen dan menerapkannya dalam pemecahan masalah matematika.
Cek di sini untuk mempelajari rumus perbandingan senilai
Contoh Soal Grafik Fungsi Eksponen Kelas 10 dan Pembahasannya
Grafik eksponen merupakan konsep penting dalam matematika, khususnya bagi siswa kelas 10. Memahami grafik eksponensial membantu dalam memecahkan berbagai masalah matematika dan aplikasi di dunia nyata. Dalam subbab ini, kami akan memberikan contoh soal tentang grafik fungsi eksponen beserta pembahasannya untuk membantu Anda memahami konsep ini secara lebih mendalam.
Contoh Soal:
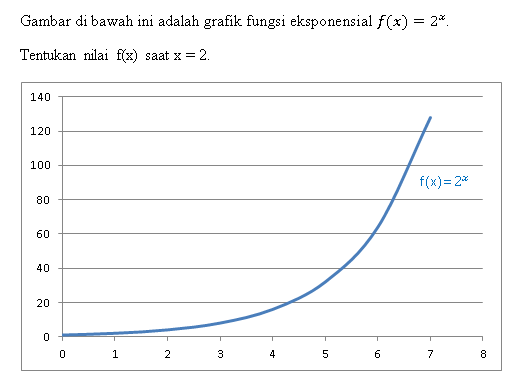
Pembahasan:
Untuk menentukan nilai f(x) saat x = 2, kita perlu melihat grafik pada titik x = 2. Dari grafik, kita melihat bahwa saat x = 2, nilai f(x) berada di sekitar 4. Jadi, f(2) = 4 .
Kesimpulan:
Dari contoh soal di atas, kita dapat melihat bagaimana grafik fungsi eksponen memperlihatkan pertumbuhan yang cepat. Dengan memahami konsep ini, Anda akan dapat menyelesaikan berbagai masalah matematika dengan lebih mudah.
Untuk memperdalam pemahaman Anda tentang grafik eksponen dan konsep matematika lainnya, jangan ragu untuk mencari bimbingan tambahan dari tutor yang berkualitas. Bersama Superprof, Anda dapat belajar dengan cepat dan efektif untuk mencapai hasil yang diinginkan.
Jangan ragu untuk mencari bantuan tambahan dari les matematika terbaik di Superprof hari ini!
Cek di sini untuk les matematika Cirebon
Ringkaskan dengan AI