Fungsi kuadrat merupakan salah satu konsep penting dalam matematika yang mulai dipelajari secara mendalam di tingkat sekolah menengah. Dalam artikel ini, kita akan membahas pengertian, rumus, dan contoh soal terkait fungsi kuadrat. Artikel ini juga akan berguna sebagai panduan untuk belajar fungsi kuadrat kelas 9, khususnya dalam mempersiapkan ujian atau tugas matematika.
Periksa di sini jika sedang mencari les matematika di Bandung
Pengertian Fungsi Kuadrat
Fungsi kuadrat adalah fungsi matematika yang variabel bebasnya memiliki pangkat tertinggi dua. Secara sederhana, fungsi kuadrat bisa dianggap sebagai fungsi yang berbentuk polinomial dengan pangkat tertinggi 2 pada variabel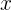 
. Rumus fungsi kuadrat bisa dituliskan sebagai:
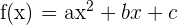
Dalam persamaan di atas,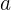 
, 
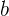, dan 
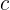disebut koefisien, dengan syarat bahwa 
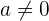(jika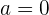 
, maka persamaan tersebut tidak lagi menjadi fungsi kuadrat, melainkan fungsi linear).
- a: Koefisien dari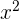 
, mempengaruhi bentuk dan arah grafik parabola.
- b: Koefisien dari 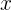, berperan dalam menentukan posisi puncak parabola.
- c: Konstanta, menentukan titik potong fungsi dengan sumbu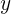 
.
Periksa di sini jika kamu ingin mempelajari rumus dilatasi dalam matematika.
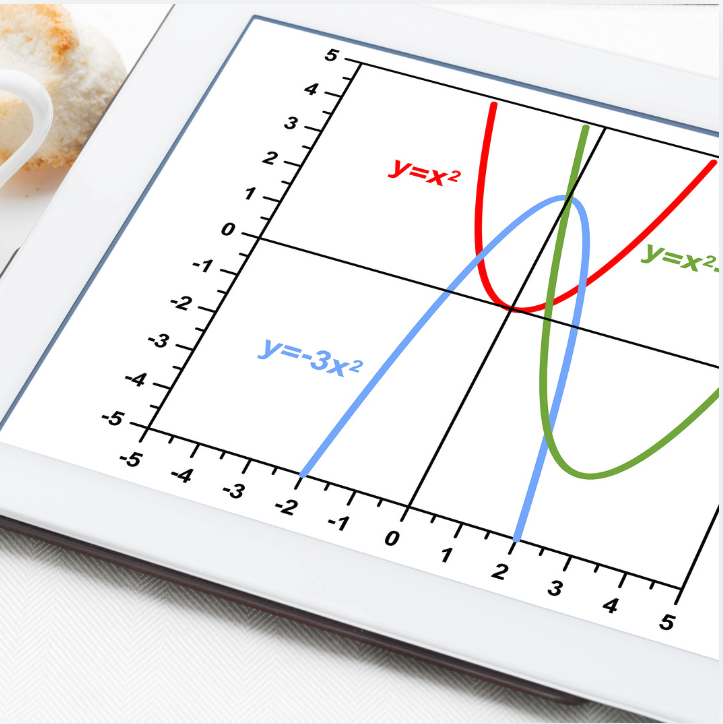
Cara Menggambar Grafik Fungsi Kuadrat
Untuk menggambar grafik dari fungsi kuadrat, langkah pertama adalah membuat tabel nilai 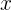dan 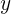. Dengan cara ini, kamu dapat menentukan beberapa titik koordinat yang nantinya akan diplot pada grafik. Setelah menentukan titik-titik tersebut, kamu bisa menggambarnya dalam bentuk parabola.
Misalnya, jika kamu memiliki fungsi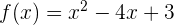 
, kamu bisa menghitung beberapa nilai 
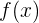untuk beberapa nilai 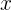. Setelah tabel dibuat, kamu bisa memplot titik-titik tersebut untuk membentuk grafik.
Ciri-Ciri Grafik Fungsi Kuadrat
Grafik fungsi kuadrat berbentuk parabola, yang bisa terbuka ke atas atau ke bawah tergantung pada tanda koefisien 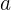. Berikut adalah beberapa ciri penting dari grafik fungsi kuadrat:
1. Grafik Simetris
Grafik fungsi kuadrat memiliki sumbu simetri yang membagi parabola menjadi dua bagian yang sama.
2. Bentuk Parabola
Parabola terbuka ke atas jika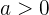 
dan terbuka ke bawah jika 
.
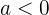3. Titik Puncak
Grafik hanya memiliki satu titik puncak, yang bisa berupa titik maksimum atau minimum.
4. Titik Potong dengan Sumbu 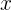dan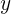
Grafik bisa memotong sumbu 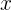dan 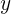tergantung nilai konstanta dan diskriminan.
Pelajari juga materi jangkauan antar kuartil
Sifat dan Rumus Grafik Fungsi Kuadrat
1. Grafik Terbuka
- Jika 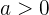, parabola terbuka ke atas dan titik puncaknya adalah nilai minimum.
- Jika 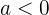, parabola terbuka ke bawah dan titik puncaknya menjadi nilai maksimum.
2. Titik Puncak (Vertex)
Rumus untuk menentukan titik puncak adalah:
- 
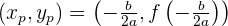
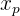: Posisi titik puncak pada sumbu .
- 
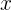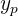: Posisi titik puncak pada sumbu .
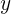3. Sumbu Simetri
Sumbu simetri adalah garis vertikal yang membagi grafik parabola menjadi dua bagian yang sama besar. Rumusnya:
Sumbu simetri ini juga menunjukkan posisi titik puncak pada sumbu .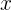
4. Titik Potong Sumbu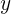
Titik potong dengan sumbu 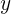terjadi ketika 
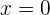. Dengan mensubstitusi 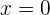ke dalam rumus fungsi, kita dapat menemukan titik ini:
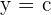
Artinya, grafik fungsi kuadrat selalu memotong sumbu 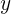di titik 
.
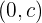5. Titik Potong Sumbu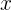
Untuk menentukan titik potong dengan sumbu 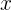, kita perlu mencari nilai 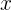saat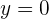 
. Persamaan fungsi kuadrat akan menjadi:
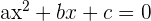
Kemudian, kamu bisa menggunakan pemfaktoran atau rumus kuadrat untuk menemukan nilai 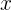. Jika terdapat dua solusi, maka grafik akan memotong sumbu 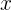di dua titik. Jika hanya satu solusi, grafik menyentuh sumbu 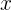di satu titik.
Cek di sini jika ingin mempelajari metode horner pada matematika
Contoh Soal Fungsi Kuadrat dan Pembahasan
1. Contoh Soal 1
Tentukan titik potong dengan sumbu 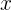dari grafik 
.
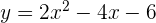Penyelesaian:
Untuk mencari titik potong dengan sumbu 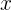, kita buat :
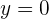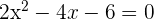
Faktorkan persamaan:
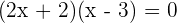
Maka,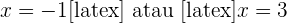 
.
Jadi, titik potongnya adalah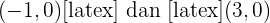 
.
2. Contoh Soal 2
Temukan titik puncak dari fungsi kuadrat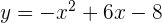 
.
Penyelesaian:
Gunakan rumus sumbu simetri untuk mencari koordinat :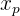
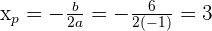
Sekarang, substitusi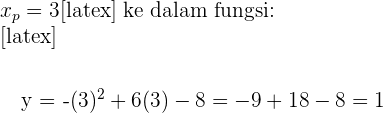 
Jadi, titik puncaknya adalah 
.
3. Contoh Soal 3
Tentukan titik potong grafik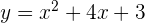 
dengan sumbu .
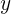Penyelesaian:
Titik potong dengan sumbu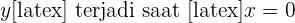 
.
Substitusi 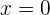ke dalam fungsi:
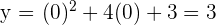
Jadi, titik potong dengan sumbu 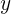adalah 
.
Fungsi kuadrat adalah salah satu konsep matematika dasar yang penting untuk dipahami. Konsep ini mengajarkan bagaimana menentukan grafik parabola, mencari titik puncak, dan memahami hubungan antara koefisien dengan bentuk grafik. Dengan latihan yang cukup, pemahaman tentang rumus grafik fungsi kuadrat dan berbagai bentuk fungsinya akan menjadi lebih mudah. Namun, jika kamu masih kesulitan memahami fungsi kuadrat kelas 9, kamu bisa meminta bantuan tutor matematika dari superprof!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
