Matematika merupakan salah satu mata pelajaran yang mungkin banyak ditakuti siswa di sekolah. Beberapa merasa bahwa matematika sesak akan rumus, dan yang lainnya kesulitan memahami materinya yang banyak. Kendati demikian, perlu Anda ketahui bahwa matematika merupakan subjek ilmu yang penting dan memiliki banyak manfaat dalam kehidupan sehari-hari. Matematika merupakan dasar bagi disiplin ilmu lainnya. Bahkan tidak mungkin bagi kita mengenal waktu, teknologi, pembangunan, dll, tanpa adanya matematika.
Ada banyak cara yang dapat dilakukan siswa sekolah untuk membantu proses belajar matematika menjadi mudah dan menyenangkan. Pertama, pilihlah tempat dan situasi yang dapat mendukung proses belajar Anda. Bangunlah suasana yang tenang dan menyenangkan agar proses belajar matematika bukan suatu hal yang menakutkan. Kedua, jika Anda kesulitan memahami materi yang dipaparkan guru di kelas, tidak ada salahnya untuk Anda mengajak teman berdiskusi bersama. Ketiga, cobalah untuk pahami rumusnya. Meskipun matematika penuh akan rumus, untuk membantu Anda dalam matematika, sebaiknya tidak menghafalkan rumus, melainkan memahami konsep rumus tersebut dan penggunaannya. Yang terpenting dalam matematika adalah jangan pernah takut salah. Anda perlu banyak mengerjakan latihan soal dan kerjakanlah secara teliti agar dapat meningkatkan kemampuan matematika Anda.
Siswa belajar matematika sejak duduk di bangku sekolah dasar hingga menyelesaikan pendidikan di perguruan tinggi. Setiap jurusan akan mempelajari matematika sebagai bagian dari pengetahuan dasar. Ada banyak materi yang diajarkan di setiap tingkatan. Salah satunya, belajar matematika kelas X yang akan membahas seputar trigonometri, barisan dan deret, statistika, fungsi invers, dan masih banyak lainnya.
Tahukah Anda apa itu fungsi invers dan bagaimana cara menentukan invers fungsi? Yuk simak penjelasan berikut ini untuk mengetahui lebih banyak.
Cek di sini jika ingin mengetahui biaya les privat matematika
Apa itu Fungsi Invers?
Pernahkah Anda mendengar tentang antonim atau kebalikan? Ya, seperti panas kebalikannya dingin, tinggi kebalikannya pendek, atau terang kebalikannya gelap. Matematika juga memiliki ilmu kebalikan yang sama. Dalam matematika, istilah kebalikan ini umumnya digunakan pada materi fungsi yang kita kenal dengan sebutan fungsi invers. Lantas apa yang dimaksud dengan fungsi invers?
Fungsi invers adalah suatu fungsi yang berkebalikan dengan fungsi asalnya. Fungsi invers ini dilambangkan dengan f-1. Tapi penting untuk Anda ketahui, invers atau kebalikan dari fungsi tidak selalu menghasilkan fungsi. Syarat agar invers fungsi merupakan fungsi invers adalah jika dan hanya jika f merupakan fungsi bijektif (korespondensi satu-satu). Atau dalam kata lain, suatu fungsi f memiliki fungsi invers (kebalikan) f-1 jika f merupakan fungsi satu-satu dan fungsi pada (bijektif). Untuk memahami lebih lanjut apa itu fungsi satu-satu, fungsi bijektif, dan bukan fungsi bijektif, simak diagram berikut.
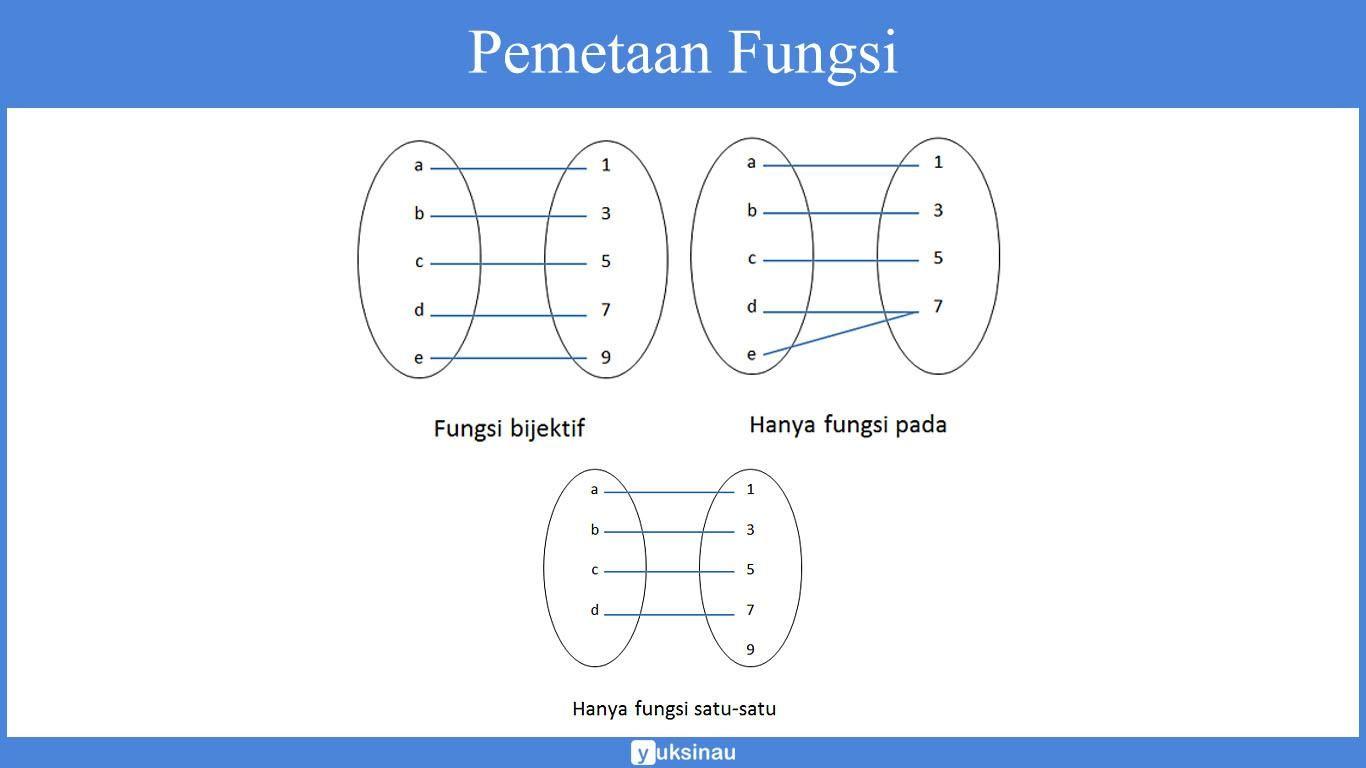
Pemetaan pertama merupakan fungsi bijektif. Fungsi bijektif terjadi ketika jumlah anggota domain sama dengan jumlah anggota kodomain. Tidak ada dua atau lebih domain berbeda dipetakan pada kodomain yang sama dan setiap kodomain memiliki pasangan di domain. Sementara pemetaan kedua dan ketiga bukan fungsi bijektif. Pada pemetaan keduahanya terjadi fungsi pada, dimana domain d dan e dipetakan ke kodomain yang sama. Dan untuk pemetaan ketiga adalah fungsi satu-satu, meskipun semua anggota domain memiliki pasangan di kodomain, tapi kodomain 9 tidak memiliki pasangan pada anggota domain. Dapatkah Anda memberi contoh fungsi bijektif lainnya? Diskusikan pada kolom komentar!
Apakah pengertian fungsi invers ada kesamaan dengan pengertian matriks?
Untuk mempermudah Anda menentukan fungsi invers, ada beberapa tahapan yang dapat diikuti. Teruslah membaca!
Cek disini untuk les matematika di medan
Cara Mencari Invers Fungsi
Anda sudah memahami definisi fungsi invers dan sekarang saatnya untuk mencari invers fungsi. Terdapat 3 tahapan yang harus dilakukan untuk mencari rumus fungsi invers, yakni:
- Ubahlah bentuk y = f(x) ke dalam bentuk x = f(y)
- Tuliskan x sebagai f-1(y) sehingga f-1(y) = f(y)
- Ubahlah variabel y dengan x sehingga didapatkan rumus fungsi invers f-1(x).
Kenali juga cara mencari nilai peluang suatu kejadian dalam artikel Kami lainnya!
Rumus Fungsi Invers
Secara singkat, fungsi invers adalah kebalikan dari fungsi asalnya, sehingga rumus fungsi invers dapat ditulis sebagai berikut:
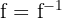
Selain itu, ada beberapa rumus fungsi invers khusus yang juga perlu untuk diketahui:
- Fungsi Linear:
- Fungsi Asal:
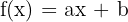, dengan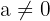 
- Fungsi Invers:
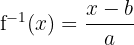
- Fungsi Asal:
- Fungsi Rasional:
- Fungsi Asal:
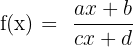, dengan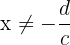 
- Fungsi Invers:
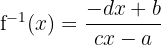, dengan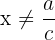 
- Fungsi Asal:
- Fungsi Kuadrat:
- Fungsi Asal:
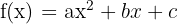, dengan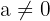 - Fungsi Invers:
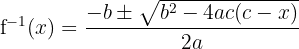
- Fungsi Asal:
- Fungsi Logaritma:
- Fungsi Asal:
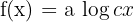, dengan a > 0, c > 0 - Fungsi Invers:
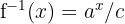
- Fungsi Asal:
- Fungsi Eksponensial:
- Fungsi Asal:
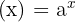, dengan a > 0 dan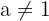 
- Fungsi Invers:
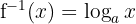
- Fungsi Asal:
Selain rumus diatas, terdapat juga beberapa rumus yang menggambarkan hubungan sifat antara rumus fungsi komposisi dan fungsi invers. Fungsi komposisi sendiri terjadi ketika dua atau lebih fungsi digabungkan menjadi satu, dan hasil dari penerapan fungsi pertama kemudian dijadikan input untuk fungsi kedua.
Salah satu rumus invers fungsi komposisi yang perlu anda diketahui adalah:
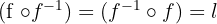
Selain itu, ada rumus lainnya yaitu fog invers :
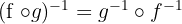
Begitu juga untuk 3 fungsi komposisi invers berikut ini:
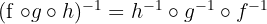
Contoh Soal Fungsi Invers
Agar anda dapat lebih paham mengenai fungsi invers perlu adanya latihan dengan contoh soal fungsi invers kelas 11. Berikut adalah 5 contoh soal fungsi invers dan jawabannya yang dapat anda pelajari agar semakin paham:
Contoh Soal Invers 1:
Tentukan fungsi invers dari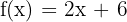 
.
Penyelesaian:
- Mulai dengan menuliskan fungsi asal:
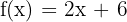
- Ganti f(x) dengan y untuk memudahkan langkah-langkahnya:
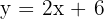
- Sekarang, ubah fungsi tersebut agar x berada di satu sisi:
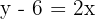
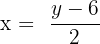
- Untuk mendapatkan fungsi invers, tukar posisi xx dan yy:
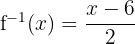
Jadi, fungsi invers dari f(x) = 2x + 6 adalah:
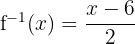
Soal Fungsi Invers 2:
Tentukan fungsi invers dari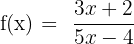 
.
Penyelesaian:
- Tulis fungsi asal:
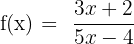
- Ganti f(x) dengan y:
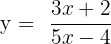
- Kalikan kedua sisi persamaan dengan 5x - 4 untuk menghilangkan penyebut:
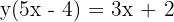
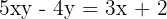
- Pindahkan semua yang mengandung x ke satu sisi:
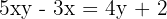
- Faktorkan x di sisi kiri:
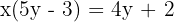
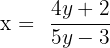
- Tukar posisi xx dan yy:
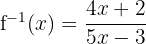
Jadi, fungsi invers dari 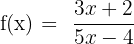adalah:
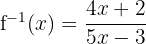
Contoh Soal Invers Fungsi 3:
Tentukan fungsi invers dari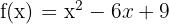 
.
Penyelesaian:
- Tulis fungsi asal:
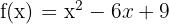
- Selesaikan menjadi kuadrat sempurna:
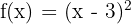
- Ganti f(x) dengan y:
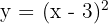
- Ambil akar kuadrat kedua sisi untuk menghilangkan pangkat dua:
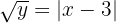
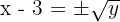
- Pindahkan 3 ke sisi kanan:
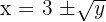
- Fungsi invers untuk bentuk kuadrat sempurna ini adalah:
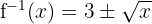
Jadi, fungsi invers dari 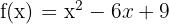adalah:
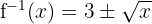
Soal Invers Fungsi 4:
Tentukan fungsi invers dari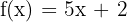 
.
Penyelesaian:
- Tulis fungsi asal:
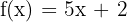
- Ganti f(x) dengan y:
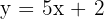
- Isolasi x:
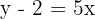
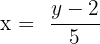
- Tukar posisi x dan y:
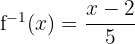
Jadi, fungsi invers dari f(x) = 5x + 2 adalah:
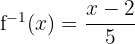
Contoh Soal Invers 5:
Tentukan fungsi invers dari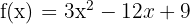 
.
Penyelesaian:
- Tulis fungsi asal:
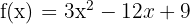
- Selesaikan menjadi kuadrat sempurna:
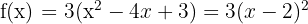
- Ganti f(x) dengan y:
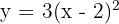
- Isolasi
:
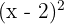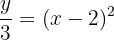
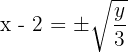
- Pindahkan 2 ke sisi kanan:
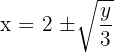
- Fungsi invers dari 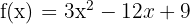adalah:
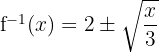
Masih Bingung Tentang Invers? Belajar dengan Tutor di Superprof Sekarang!
Mempelajari rumus fungsi invers memang penting, tetapi jika anda merasa masih bingung atau ingin memperdalam pemahaman, tidak ada salahnya untuk belajar lebih lanjut dengan tutor privat yang ahli! Di Superprof, anda bisa menemukan banyak tutor matematika yang siap membantu anda memahami konsep-konsep rumit seperti fungsi komposisi invers ini dengan cara yang menyenangkan dan mudah dipahami.
Jadi, tunggu apa lagi? Segera cari tutor terbaik di Superprof dan tingkatkan kemampuan matematika anda sekarang juga!
Jika materi ini masih terasa sulit, cobalah belajar tentang persamaan lingkaran! Itu cenderung lebih mudah dipelajari.
Atau jika Anda perlu materi yang lebih menantang, silakan pelajari tentang aturan trigonometri! Selamat belajar!
Apa Anda menyukai artikel ini? Berikan penilaian Anda
Loading...
