Apa yang Anda ingat tentang materi persamaan kuadrat? Tahukah Anda cara mencari diskriminan persamaan kuadrat? Bagaimana rumus diskriminan? Ya, persamaan kuadrat merupakan materi wajib yang diajarkan pada siswa sejak bangku SMP, dan diskriminan akan dibahas pada kelas 9.
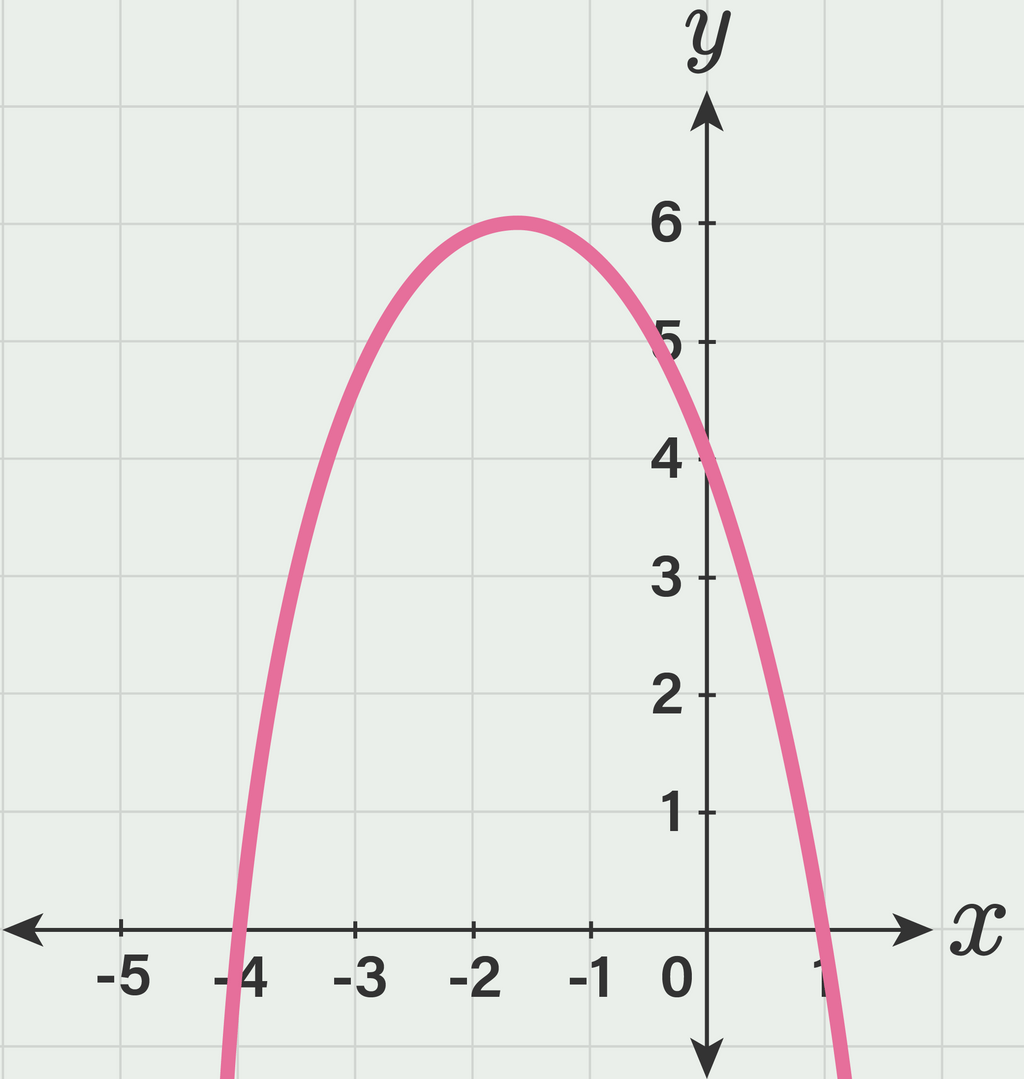
Fungsi kuadrat memiliki solusi atau akar persamaan yang digambarkan dalam nilai d. Nilai d disebut juga sebagai diskriminan, dan memiliki pengaruh pada fungsi kuadrat dan juga grafik fungsinya.
Agar membantu Anda memahami apa itu diskriminan dan rumus d, teruslah membaca! Kami berusaha untuk membantu Anda belajar matematika lebih mudah. Namun untuk memastikan kemajuan secara signifikan dan konsisten, tidak ada yang lebih baik selain belajar bersama guru privat Superprof.
Mari kita lihat pengertian diskriminan, rumus d, dan beberapa contoh soal untuk membantu Anda memahami cara kerjanya.
Periksa di sini untuk mengetahui cara mencari rata rata data kelompok

Apa yang dimaksud dengan diskriminan?
Sebelum membahas tentang mencari nilai d pada persamaan kuadrat, hal utama yang harus Anda pahami adalah pengertian dari diskriminan.
Dalam matematika, diskriminan adalah suatu nilai yang menjadi penentu sifat-sifat dari akar suatu persamaan kuadrat. Dengan nilai d 0, bisa menentukan apakah suatu bentuk persamaan kuadrat memiliki penyelesaian berupa akar real atau tidak. Diskriminan juga memiliki pengertian hubungan antara koefisien dalam persamaan kuadrat untuk mencari akar persamaan dan ciri-ciri yang lainnya.
Secara umum, diskriminan adalah suatu nilai pada persamaan kuadrat yang membedakan banyaknya akar persamaan itu sendiri.
Dikutip dari Buku Ajar Matematika Dasar untuk Perguruan Tinggi oleh Sri Jumini, kegunaan diskriminan adalah untuk menentukan jenis akar-akar persamaan kuadrat. Maka dengan mengetahui nilai diskriminan, kita dapat melihat jenis akar dari persamaan kuadrat tersebut.
Sementara, persamaan kuadrat adalah suatu persamaan yang berbentuk ax^2 + bx + c = 0, dengan a, b, dan c sebagai konstanta yang bersesuaian dengan persamaan kuadrat.
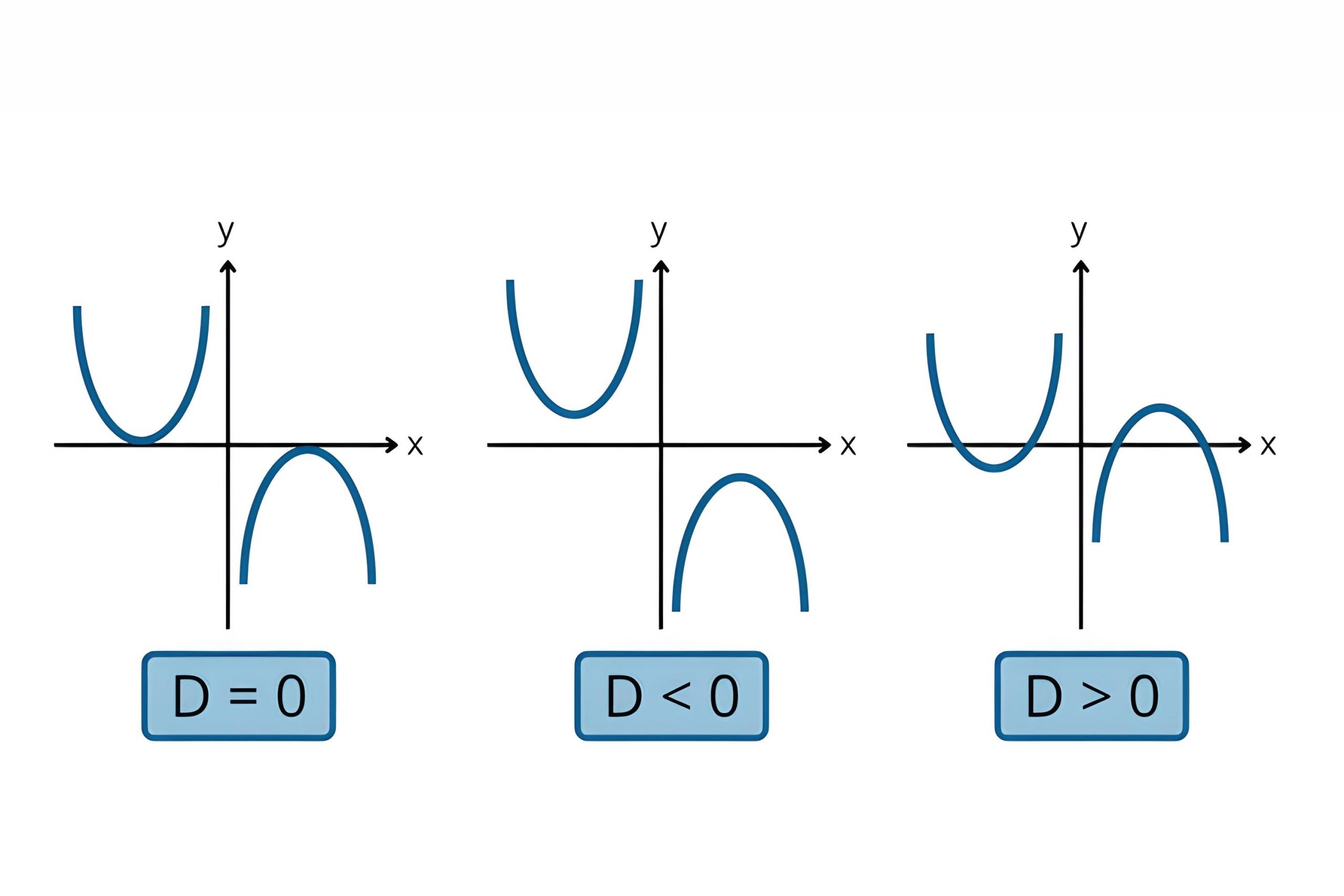
Dilansir dari Khan Academy, diskriminan bisa bernilai poritif, negatif, atau nol yang menentukan berapa solusi untuk persamaan kuadrat yang ada. Berikut sifat dan fungsi diskriminan pada persamaan kuadrat ax^2 + bx + c = 0, dengan a ≠ 0.
Cek di sini untuk les matematika terdekat
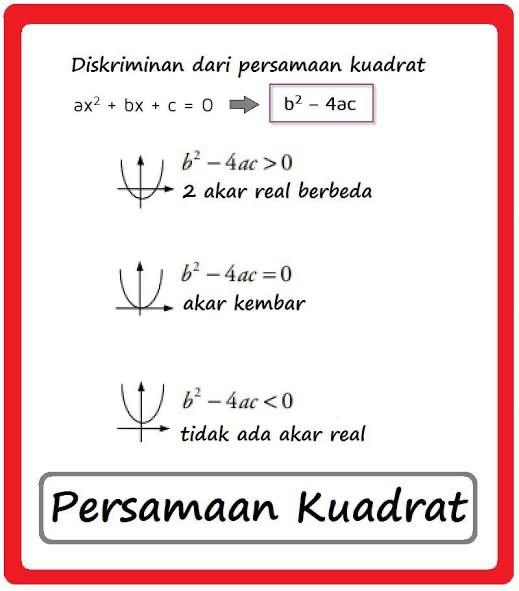
Diskriminan positif (D > 0)
Jika diskriminan bernilai positif (1 hingga ∞), maka persamaan kuadrat tersebut memiliki dua solusi. Kedua solusi tersebut berupa bilangan real (akar nyata) yang nilainya berbeda satu sama lain (x1 ≠ x2).
Diskriminan nol (D = 0)
Jika diskriminan bernilai nol (0), maka persamaan kuadrat memiliki dua solusi. Namun, kedua solusi tersebut berupa bilangan real (akar nyata) dengan nilai yang sama (x1 = x2). Sehingga, dapat disebut bahwa persamaan kuadrat hanya memiliki satu solusi.
Diskriminan negatif (D < 0)
Adapun, jika diskriminan bernilai negatif (-1 hingga -∞), maka persamaan kuadrat tidak memiliki solusi. Hal tersebut karena diskriminan negatif menunjukkan tidak adanya akar nyata dan hanya akar imajiner yang tidak real.
Lantas bagaimana kita dapat mencari nilai diskriminan? Rumus diskriminan diperoleh dari rumus ABC.
Anda perlu juga mengetahui pengertian dari integral tak tentu!
Rumus Diskriminan
Untuk mengetahui akar-akar dari persamaan kuadrat ax^2 + bx + c = 0, maka Anda dapat menggunakan rumus ABC. Apakah Anda masih mengingat rumus ABC?
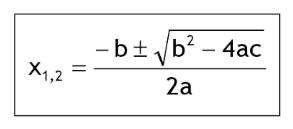
Rumus diskriminan ini dapat ditemukan dalam rumus ABC. Rumus diskriminan adalah seperti di bawah ini, dengan a, b, dan c sebagai konstanta yang bersesuaian dengan persamaan kuadrat.
D = b² – 4ac
Dengan,
D: nilai diskriminan
b: koefisien variabel x persamaan kuadrat
a: koefisien variabel x² persamaan kudrat
c: konstanta persamaan kuadrat
Dengan demikian, rumus ABC dapat menjadi sebagai berikut ketika diketahui nilai diskriminannya;
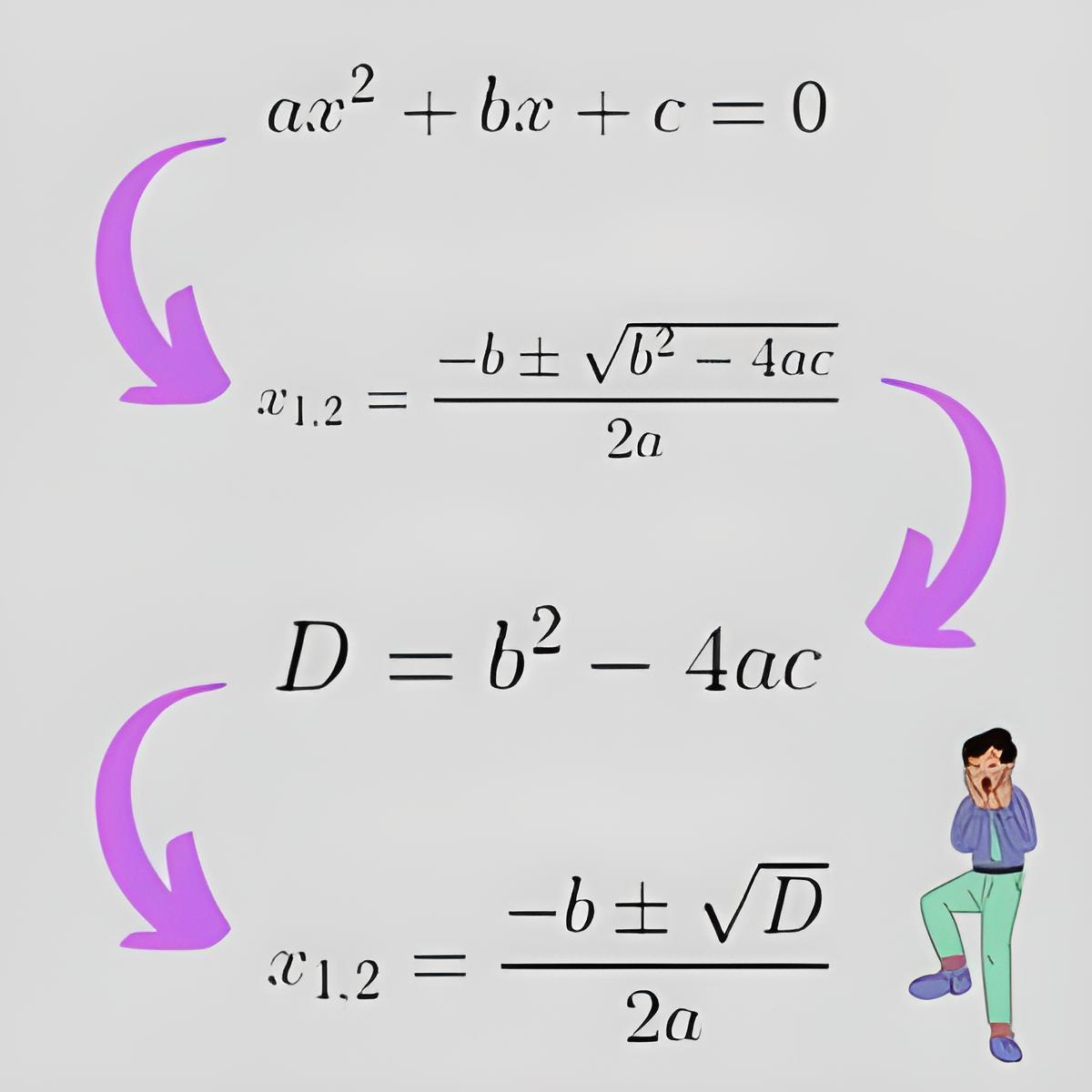
Maka dapat disimpulkan;
Pemberian istilah diskriminan D = b2 - 4ac, karena nilai D = b2 - 4ac ini yang telah mendiskriminasikan (membedakan) jenis akar-akar persamaan kuadrat. Apakah Anda sudah memahami makna diskrimanan dan rumus diskriminan? Mudah, bukan? Untuk melatih Anda, beberapa contoh soal berikut dapat Anda pahami lebih lanjut.
Periksa di sini jika ingin mengetahui apa itu simpangan baku
Contoh Soal
Memahami konsep matematika tidak bisa hanya mengandalkan teori saja, latihan soal merupakan cara untuk mengukur pemahaman kita terhadap materi matematika. Ini juga termasuk dalam materi diskriminan, Anda dapat melihat pemahaman Anda dalam menentukan rumus d dengan mencoba beberapa contoh soal berikut ini.
Berikut beberapa contoh soal diskriminan.
Contoh Soal 1
Dari persamaan kuadrat x^2 - 10x + 16 = 0, tentukan diskriminan dan jenis akarnya!
Jawab:
Dari persamaan kuadrat; x^2 - 10x + 16 = 0,
Berarti a = 1,
b = 10,
c = 16
Maka dapat dicari untuk nilai diskrimiannya adalah sebagai berikut.
D = b^2 - 4ac
= (-10)^2 - 4 . 1 . 16
= 100 - 64
= 36
Jadi, nilai diskriminannya adalah 36. Karena D > 0 yakni (36 > 0), maka persamaan kuadrat x^2 - 10x + 16 = 0 mempunyai akar-akar rasional.
Cek di sini untuk mengetahui statistika deskriptif
Contoh Soal 2
Tentukan apakah persamaan kuadrat x^2 + 4x + 4 = 0 memiliki akar-akar real, akar kembar, atau akar imajiner, dan hitunglah diskriminannya.
Jawaban:
Dari persamaan x^2 + 4x + 4 = 0, maka diketahui;
a = 1
b = 4
c = 4
Maka dapat dicari untuk nilai diskrimiannya adalah sebagai berikut.
D = b^2 - 4ac
D = (4)^2 - 4(1)(4) = 16 - 16 = 0.
Nilai diskriminan dari persamaan x^2 + 4x + 4 = 0 adalah 0. Karena diskriminan adalah 0 (d 0), maka persamaan x^2 + 4x + 4 = 0 memiliki akar kembar.
Contoh soal 3:
Tentukan nilai diskriminan dari persamaan kuadrat berikut ini 2x^2 + 6x + 8 = 0
Diketahui:
Dari persamaan 2x^2 + 6x + 8 = 0, diketahui;
a = 2
b = 6
c = 8
Maka dapat dicari untuk nilai diskrimiannya adalah sebagai berikut.
D = b^2 – 4ac
D = 6^2 – 4 . 2 . 8
D = 36 – 64 = -28
Jadi, nilai diskriminannya adalah -28. Karena D < 0 yakni (-28 > 0), maka persamaan kuadrat 2x^2 + 6x + 8 = 0 tidak memiliki solusi. Hal tersebut karena diskriminan negatif menunjukkan tidak adanya akar nyata dan hanya akar imajiner yang tidak real.
Untuk membantu Anda belajar lebih mudah dan cepat, kami sarankan untuk meminta bantuan kepada guru privat Superprof. Guru privat terbaik dapat merancang program belajar yang menyenangkan dan mudah bagi Anda.
Periksa di sini untuk les privat matematika Jakarta Timur
Ringkaskan dengan AI















