Matematika merupakan mata pelajaran yang menyenangkan dan memiliki banyak manfaat dalam kehidupan sehari-hari. Jika dilihat dari fungsinya, bahkan matematika disebut juga sebagai “Queen and Servant of Science”, maksudnya adalah matematika selain sebagai fondasi bagi ilmu pengetahuan lain juga sebagai pembantu bagi ilmu pengetahuan yang lain, khususnya dalam pengembangan ilmu pengetahuan tersebut. Lantas, apa materi matematika yang menjadi favorit Anda? Aljabar, trigonometri, integral, persamaan kuadrat? Atau mungkin Anda menyukai perhitungan statistika? Ya, statistika merupakan salah satu subbab yang dapat dengan mudah kita lihat penerapannya dalam kehidupan sehari-hari.
Jika sebelumnya Anda sudah belajar cara mencari mean, modus, dan median dalam data tunggal, sekarang mari kita berfokus pada cara menghitung rata rata data kelompok. Pada dasarnya, mencari rata rata data kelompok dapat dilakukan dengan tiga cara, yakni tiga rumus rata-rata data kelompok yang terdiri dari rumus titik tengah, rumus simpangan rata rata sementara, dan rumus kode atau koding. Jangan khawatir, meskipun terdengar sedikit rumit, rumus rata rata data kelompok akan lebih mudah dipahami dengan contoh soal dan pembahasan berikut ini!
Untuk membantu Anda belajar matematika lebih cepat dan menyenangkan, kursus privat Superprof akan membantu Anda.
Cek di sini jika sedang mencari guru matematika

Mencari rata rata data kelompok

Dalam penyajian data, terdapat ukuran pemusatan data yang mewakili keseluruhan data yang telah diperoleh. Ukuran pemusatan data ini terdiri dari mean, median, modus.
Dikutip dari Buku Ajar Matematika SD Kelas Tinggi (2021), mean adalah nilai rata-rata dari beberapa buah data. Nilai mean dapat diperoleh dengan membagi jumlah data dengan banyaknya data.
Mean cukup sering digunakan dalam mengolah data, misalnya untuk menentukan nilai ulangan dimana hasil mean akan diperlihatkan ketika akan menentukan berapa banyak siswa yang mendapat nilai diatas rata-rata nilai di dalam suatu kelas.
Untuk memperoleh rata-rata, ada dua rumus yang digunakan tergantung dari jenis data, yakni rata rata data tunggal dan rata rata data kelompok. Perlu diingat bahwa data kelompok adalah bentuk penyajian data yang biasanya dalam tabel dan memiliki interval tertentu. Dilansir dari Idschool, rata rata data kelompok merupakan representasi nilai yang terdapat pada suatu data yang disajikan dalam bentuk kelompok. Ada tiga cara mencari rata-rata data kelompok, yaitu dengan menggunakan titik tengah, menggunakan simpangan rata-rata sementara dan menggunakan kode (coding). Untuk lebih jelasnya, perhatikan rumus rata rata data kelompok berikut ini.
Cara 1; Rumus Titik Tengah
Cara pertama merupakan cara biasa yang mungkin paling umum digunakan, rumus rata rata data kelompok dengan menggunakan titik tengah adalah sebagai berikut;
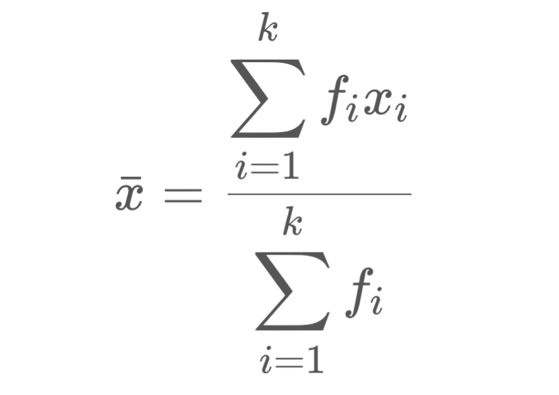
Keterangan;
xˉ = rata-rata hitungdata berkelompok
fi = frekuensi data kelas ke-i
xi = nilai tengah kelas ke-i
Berikut contoh soal cara menghitung rata rata data kelompok menggunakan tiga cara, dimulai dari rumus titik tengah.
Soal:
Sebanyak 21 orang pekerja dijadikan sampel dan dihitung tinggi badannya. Data tinggi badan dibuat dalam bentuk kelas-kelas interval. Hasil pengukuran tinggi badan adalah sebagai berikut.
| Tinggi Badan | Frekuensi (fi)(fi) |
|---|---|
| 151 - 155 | 3 |
| 156 - 160 | 4 |
| 161 - 165 | 4 |
| 166 - 170 | 5 |
| 171 - 175 | 3 |
| 176 - 180 | 2 |
Hitunglah rata-rata tinggi badan pekerja dengan menggunakan rumus titik tengah!
Jawab;
Proses penghitungan rata-rata dengan menggunakan titik tengah dibantu dengan menggunakan tabel di bawah ini.
| Tinggi Badan | Titik Tengah (xi)(xi) | Frekuensi (fi)(fi) | fi⋅xifi⋅xi |
|---|---|---|---|
| 151 - 155 | 153 | 3 | 459 |
| 156 - 160 | 158 | 4 | 632 |
| 161 - 165 | 163 | 4 | 652 |
| 166 - 170 | 168 | 5 | 840 |
| 171 - 175 | 173 | 3 | 519 |
| 176 - 180 | 178 | 2 | 356 |
| Jumlah | 21 | 3458 |
Dari tabel di atas diperoleh
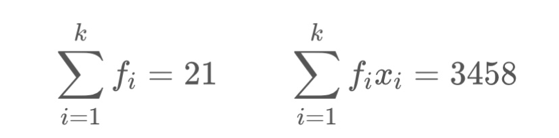
Dengan begitu dapat kita hitung rata-rata data berkelompok sebagai berikut
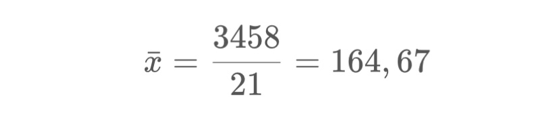
Cara 2; Rumus Simpangan Rata rata Sementara
Rumus kedua menggunakan simpangan rata rata sementara
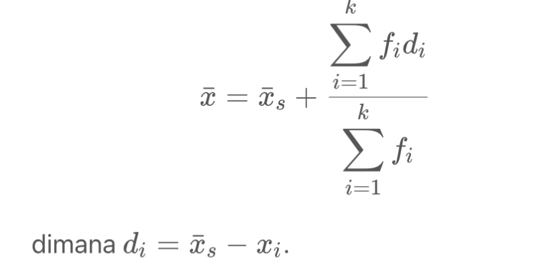
Untuk membantu Anda memahami perbedaannya, mari kita kerjakan soal yang sama seperti di atas tapi menggunakan rumus simpangan rata rata sementara!
Soal:
Sebanyak 21 orang pekerja dijadikan sampel dan dihitung tinggi badannya. Data tinggi badan dibuat dalam bentuk kelas-kelas interval. Hasil pengukuran tinggi badan adalah sebagai berikut.
| Tinggi Badan | Frekuensi (fi)(fi) |
|---|---|
| 151 - 155 | 3 |
| 156 - 160 | 4 |
| 161 - 165 | 4 |
| 166 - 170 | 5 |
| 171 - 175 | 3 |
| 176 - 180 | 2 |
Hitunglah rata-rata tinggi badan pekerja dengan menggunakan rumus simpangan rata rata sementara!
Dengan menggunakan rumus 2:
Sebelum menghitung rata-rata data berkelompok menggunakan simpangan rata-rata sementara, kita terlebih dahulu menetapkan rata-rata sementaranya. Misalkan rata-rata sementara yang kita tetapkan adalah 160. Selanjutnya kita bisa membuat tabel penghitungan sebagai berikut.
| Tinggi Badan | Titik Tengah (xi)(xi) | Frekuensi (fi)(fi) | di=di= 160−xi160−xi | f1⋅dif1⋅di |
|---|---|---|---|---|
| 151 - 155 | 153 | 3 | -7 | -21 |
| 156 - 160 | 158 | 4 | -2 | -8 |
| 161 - 165 | 163 | 4 | 3 | 12 |
| 166 - 170 | 168 | 5 | 8 | 40 |
| 171 - 175 | 173 | 3 | 13 | 39 |
| 176 - 180 | 178 | 2 | 18 | 36 |
| Jumlah | 21 | 98 |
Dari tabel di atas diperoleh
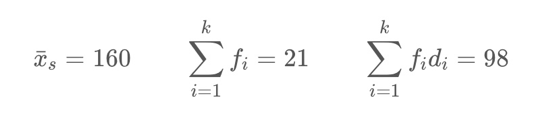
Hasil rata-rata data kelompok hitung menggunakan simpangan rata-rata adalah
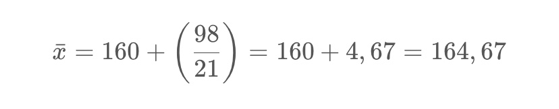

Jika Anda belum mengerti tentang simpangan baku, Silahkan baca artikel Kami lainnya!
Cara 3; Rumus Kode atau Koding
Dengan soal yang sama, mari kita coba mencari rata-rata data kelompok menggunakan rumus koding, sebagai berikut.
Sama dengan menggunakan simpangan rata-rata sementara, sebelum menghitung rata-rata dengan cara coding, kita juga harus menetapkan rata-rata sementara. Namun rata-rata sementara yang kita tetapkan harus sama dengan salah satu nilai tengah salah satu kelas interval.
Misalkan kita menetapkan rata-rata sementara adalah nilai tengah kelas keempat, yaitu 168. Dengan begitu kita bisa membuat tabel dan pengkodean seperti di bawah ini.
| Tinggi Badan | Titik Tengah (xi)(xi) | Frekuensi (fi)(fi) | Coding (ci)(ci) | f1⋅cif1⋅ci |
|---|---|---|---|---|
| 151 - 155 | 153 | 3 | -3 | -9 |
| 156 - 160 | 158 | 4 | -2 | -8 |
| 161 - 165 | 163 | 4 | -1 | -4 |
| 166 - 170 | 168 | 5 | 0 | 0 |
| 171 - 175 | 173 | 3 | 1 | 3 |
| 176 - 180 | 178 | 2 | 2 | 4 |
| Jumlah | 21 |
Pengkodean dimulai dari angka 0 untuk kelas interval dimana rata-rata sementara ditetapkan. Kemudian dengan kelas sebelumnya berturut-turut menjadi angka negatif (-1, -2, -3 dan seterusnya) menjauhi kelas rata-rata sementara. Berikutnya dengan kelas sesudahnya berturut-turut pengkodeannya menjadi angka positif (1,2 3 dan seterusnya) menjauhi kelas rata-rata sementara tersebut.
Dari tabel di atas diperoleh
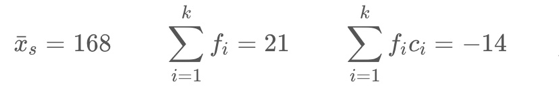
Hasil rata-rata hitung menggunakan coding adalah sebagai berikut.
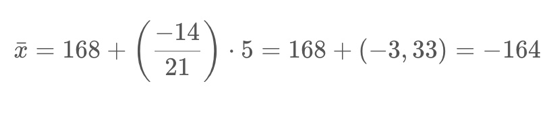
Dari ketiga cara di atas, manakah yang mudah menurut Anda? Rumus titik tengah dan rumus simpangan rata-rata sementara yang paling sering digunakan. Tapi bagaimanapun, matematika akan lebih mudah jika Anda banyak berlatih. Ikuti kursus privat matematika bersama Superprof untuk membantu Anda belajar lebih mudah dan menyenangkan.

Ringkaskan dengan AI















