Dalam matematika sekolah, tentu sudah tidak asing bagi Anda dengan istilah ‘bilangan’ bukan? Bilangan merupakan suatu konsep matematika yang memberikan nilai jumlah terhadap sesuatu yang dihitung. Itu mengapa bilangan digunakan dalam pengukuran dan pencacahan.
Bilangan terdiri dari berbagai macam, bilangan asli, bilangan cacah, bilangan ganjil, bilangan genap, bilangan imajiner, bilangan real, dan bilangan bulat. Tapi, apa yang Anda ketahui dari sejarah bilangan? Diperkirakan, awal mula munculnya bilangan dari bangsa atau suku-suku yang bermukim di sepanjang aliran sungai. Seperti Bangsa Mesir di Sungai Nil, Bangsa Babilonia di Sungai Tigris dan Eufrat, Bangsa Cina di Sungai Huang Ho dan Yangtze, dan masih banyak lainnya. Bilangan matematika pada saat itu digunakan untuk perhitungan perdagangan, pengukuran luas tanah, perubahan musim, dan lain sebagainya.
Kita dapat melihat bagaimana matematika sangat dekat dengan kehidupan sehari-hari kita.
Mari kita lihat lebih jauh tentang pengertian bilangan bulat, bagaimana cara membandingkan bilangan bulat, dan operasi bilangan bulat.
Meski matematika mungkin pelajaran yang membosankan dengan banyaknya rumus yang harus diingat, kami akan memberi panduan sederhana untuk membantu Anda belajar lebih mudah. Teruslah membaca!
Cek di sini untuk les matematika terdekat

Apa Yang Dimaksud Dengan Bilangan Bulat?
Apakah Anda berfikir bahwa bilangan bulat adalah kumpulan atau himpunan bilangan yang bentuknya bulat? Tentu saja bukan! Sederhananya, bilangan bulat adalah kumpulan bilangan yang nilainya bulat, bukan dalam bentuk desimal maupun pecahan.
Bilangan bulat terdiri dari bilangan cacah dan bilangan bulat negatif. Himpunan bilangan bulat sendiri dapat dilambangkan dengan huruf Z yang berasal dari kata Zahlen (dalam bahasa Jerman) yang artinya adalah bilangan.
Dapatkah Anda sebutkan, bilangan apa yang termasuk bilangan cacah? Bilangan cacah terdiri dari nol dan bilangan bulat positif. Maka dapat disimpulkan bahwa bilangan bulat terdiri dari bilangan nol, bilangan asli, bilangan bulat negatif. Bilangan asli atau bilangan bulat positif terdiri dari bilangan 1,2,3,4,... dst. Jika ingin dibagi lagi, bilangan asli juga terdiri dari bilangan ganjil, bilangan genap, bilangan prima, dan bilangan komposit.
- Bilangan ganjil merupakan himpunan bilangan asli yang nilainya tidak habis dibagi dua.
- Bilangan genap merupakan himpunan bilangan asli yang nilainya habis dibagi dua.
- Bilangan prima merupakan himpunan bilangan asli yang lebih dari 1 dan hanya bisa dibagi dengan angka 1 atau bilangan itu sendiri.
- Bilangan komposit merupakan himpunan bilangan asli yang lebih dari 1 dan tidak termasuk bilangan prima.
Berikut contoh bilangan bulat yang paling mudah dipahami dan sering ditemui dalam kehidupan sehari-hari:
- Bilangan Buat Positif (… 1, 2, 3, 10, 250, …)
Contohnya:
- 5 (jumlah buku di rak)
- 12 (jumlah siswa di kelas)
- 100 (jumlah uang tanpa pecahan desimal)
- Bilangan Nol (0)
Contohnya:
- 0 (jumlah barang yang tersisa)
- 0 derajat (titik antara suhu panas dan dingin)
- Bilangan Bulat Negatif (… –1, –2, –3, –10, –50, …)
Contohnya:
- –3°C (suhu rendah di daerah bersalju)
- –1 (lantai basement di sebuah gedung)
- –20 (saldo minus pada laporan keuangan)
Untuk lebih memahami konsep bilangan tersebut, coba perhatikan garis bilangan di bawah ini.
Cek di sini untuk les matematika SD terdekat
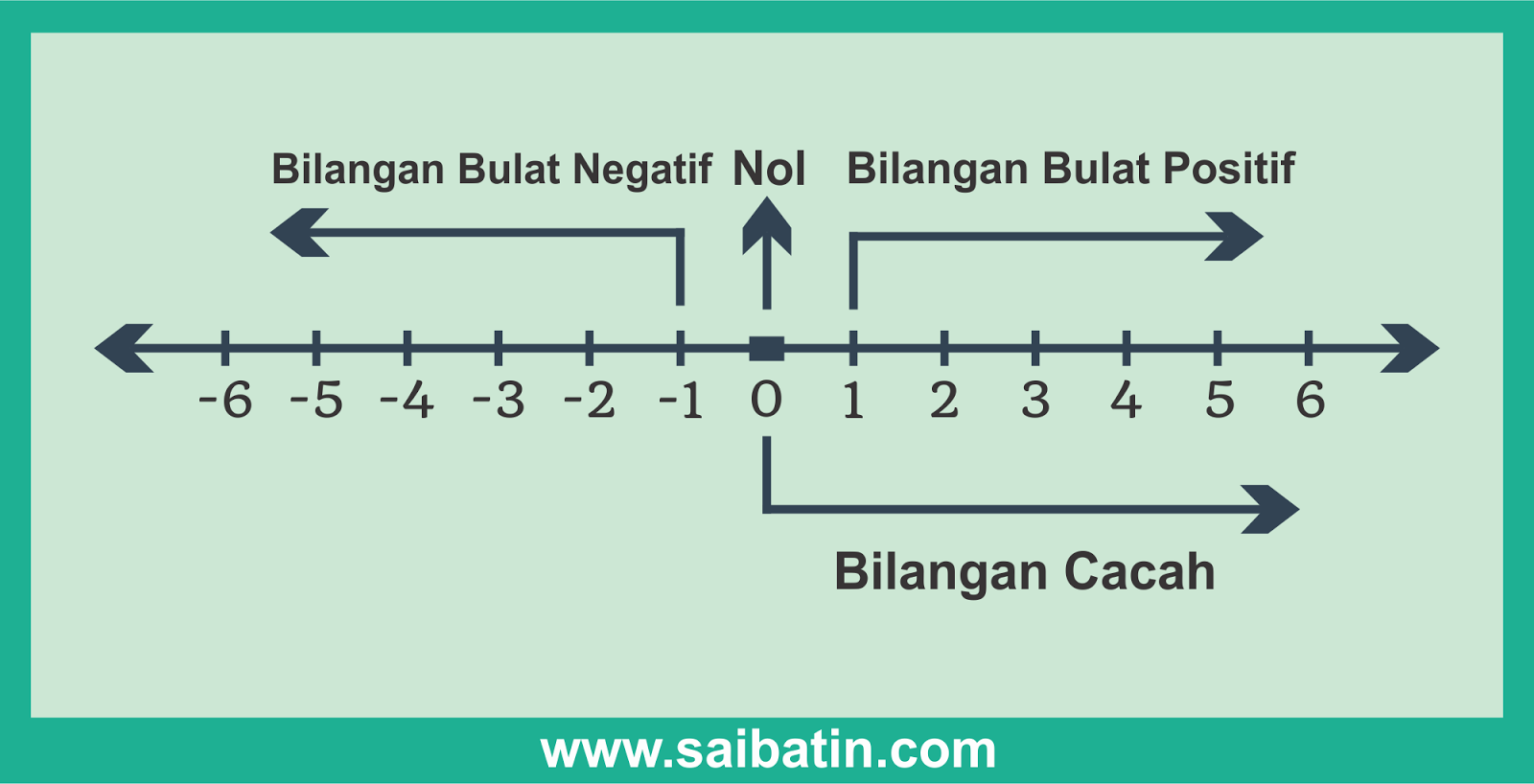
Bilangan bulat = { ..., -3, -2, -1, 0, 1, 2, 3, ...}
Bilangan bulat negatif = { -1, -2, -3, -4, ...}
Bilangan cacah = { 0, 1, 2, 3, 4, ...}
Bilangan asli = {1, 2, 3, 4, 5, ...}
Bilangan genap = {2, 4, 6, 8, ...}
Bilangan ganjil = {1, 3, 5, 7, 9, ...}
Bilangan prima = {2, 3, 5, 7, 11, ....}
Bilangan komposit = {4, 6, 8, 9, 10}
Dari sini, cobalah untuk menjawab latihan soal berikut!
A = {7, 11, 17, 19,23, 29, 31} Himpunan bilangan A tersebut termasuk ke dalam bilangan?
Cek di sini untuk kursus statistik di Bandung
Macam-Macam Bilangan Bulat
Bilangan bulat memiliki beberapa kategori, mulai dari bilangan cacah hingga bilangan negatif. Berikut penjelasannya satu per satu.
1. Bilangan Cacah
Bilangan cacah merupakan kumpulan angka yang terdiri dari nol dan bilangan bulat positif. Kelompok ini sering disebut sebagai bilangan bulat “tidak negatif”, karena seluruh anggotanya bernilai positif atau nol.
Simbol bilangan cacah adalah W (Whole Numbers). Contohnya: 0, 1, 2, 3, 4, 5, dan seterusnya.
2. Bilangan Nol
Apakah 0 Bilangan Bulat?
Ya, 0 termasuk bilangan bulat. Bilangan bulat mencakup semua bilangan negatif, nol, dan bilangan positif. Dalam himpunan bilangan bulat, nol berperan sebagai titik tengah antara bilangan negatif dan positif.
Sesuai namanya, bilangan nol adalah angka yang menyatakan nilai kosong. Angka ini termasuk dalam bilangan cacah dan hanya memiliki satu unsur, yaitu 0. Keberadaan 0 penting dalam berbagai operasi bilangan bulat, seperti penjumlahan, pengurangan, dan garis bilangan bulat. Misalnya, saat menjumlahkan –3 + 3, hasilnya 0, menunjukkan nol sebagai nilai netral dalam operasi matematika.
3. Bilangan Bulat Positif (Bilangan Asli)
Bilangan bulat positif, atau bilangan asli, adalah himpunan bilangan bulat yang bernilai di atas nol. Kelompok ini juga merupakan bagian dari bilangan cacah.
Bilangan asli dilambangkan dengan N (Natural Numbers). Contoh: 1, 2, 3, 4, 5, dan seterusnya.
4. Bilangan Bulat Negatif
Berbanding terbalik dengan bilangan asli, kelompok ini mencakup bilangan bulat yang bernilai kurang dari nol. Contoh: …, -5, -4, -3, -2, -1.
5. Bilangan Ganjil
Bilangan ganjil adalah bilangan yang tidak dapat dibagi 2 dengan hasil yang tepat (masih memiliki sisa).
Contoh himpunan: {…, -7, -5, -3, -1, 1, 3, 5, 7, …}
6. Bilangan Genap
Bilangan genap adalah kebalikan dari bilangan ganjil, yaitu bilangan yang merupakan kelipatan 2 atau habis dibagi 2 tanpa sisa.
Contoh himpunan: {…, -6, -4, -2, 0, 2, 4, 6, 8, 10, …}
Untuk contoh:
- 8 adalah bilangan genap karena saat dibagi 2 hasilnya tepat.
- 13 tidak habis dibagi 2, sehingga termasuk bilangan ganjil.
7. Bilangan Prima
Bilangan prima adalah bilangan lebih besar dari 1 yang hanya bisa dibagi oleh 1 dan dirinya sendiri.
Contoh: 2, 3, 5, 7, 11, 13, …
Sebagai contoh:
- 2 adalah bilangan prima karena hanya bisa dibagi 1 dan 2.
- 4 bukan bilangan prima karena bisa dibagi 1, 2, dan 4.
8. Bilangan Komposit
Bilangan komposit adalah bilangan lebih besar dari 1 dan bukan termasuk bilangan prima, karena memiliki lebih dari dua faktor.
Contoh: 4, 6, 8, 9, 10, 12, …
Sebagai contoh:
- 4 adalah bilangan komposit karena dapat dibagi 1, 2, dan 4.
- 6 juga komposit karena memiliki beberapa faktor: 1, 2, 3, dan 6.
Bagaimana Membandingkan Bilangan Bulat?
Sebelumnya, tahukah Anda siapa penemu bilangan bulat? Kita mengetahui bahwa bilangan sudah sejak lama digunakan oleh bangsa atau suku-suku yang tinggal di sepanjang aliran sungai, tapi yang merumuskan adalah matematikawan asal Italia yang bernama Leonardo da Pisa atau lebih dikenal dengan sebutan Fibonacci.
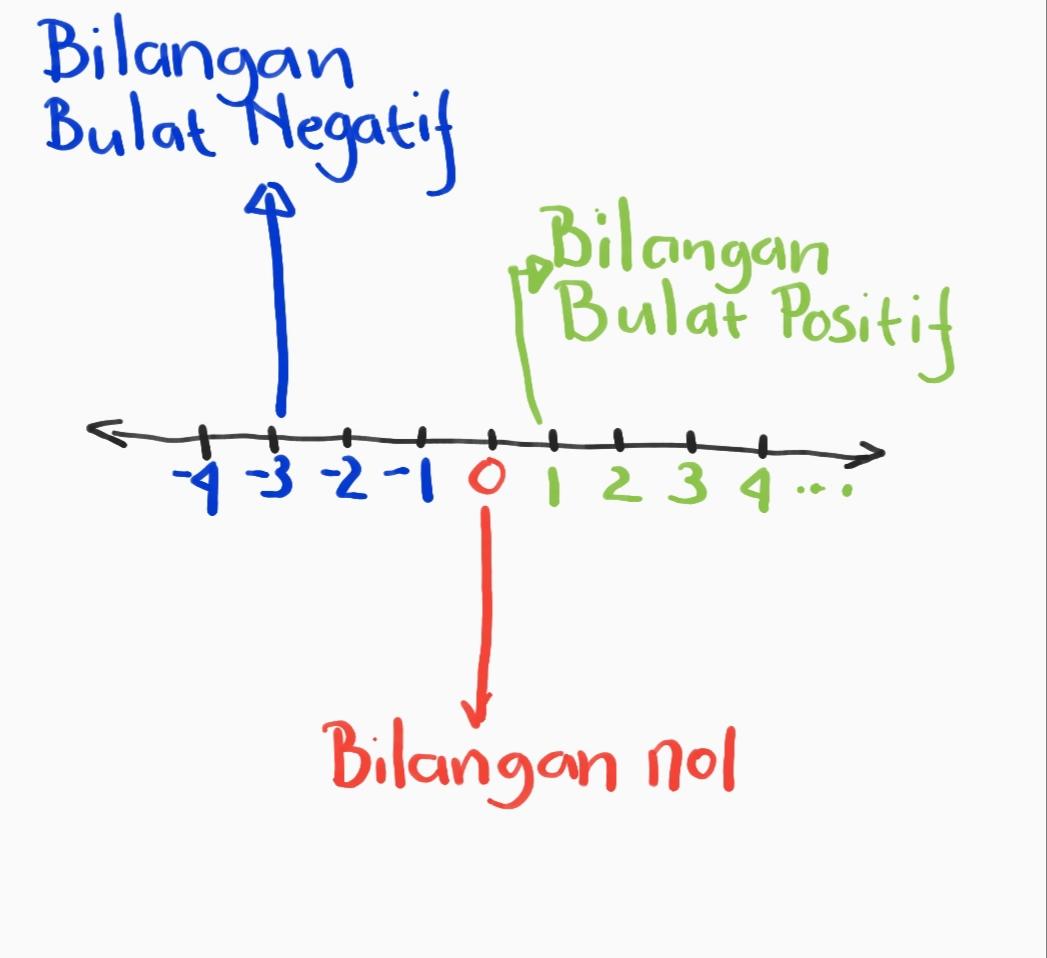
Setelah Anda memahami apa itu bilangan bulat, mari kita belajar cara membandingkan bilangan bulat.
Membandingkan bilangan bulat berarti menetukan apakah suatu bilangan memiliki nilai lebih besar, lebih kecil, atau sama dengan bilangan bulat yang lain. Untuk lebih memahaminya, Anda dapat mulai mengurutkan bilangan bulat dari yang terkecil hingga terbesar atau sebaliknya. Berdasarkan garis bilangan, semakin ke kanan letak suatu bilangan, maka nilainya semakin besar. Sementara, semakin ke kiri letak bilangan tersebut, maka nilainya semakin kecil.
Atau dapat diartikan, pada bilangan bulat negatif, semakin besar bilangannya maka semakin kecil nilainya! Berkebalikan dengan bilangan bulat positif, semakin besar bilangannya, semakin besar juga nilainya.
Dalam membandingkan bilangan bulat, Anda juga perlu memahami tanda-tanda berikut.
Misalkan terdapat dua bilangan bulat, a dan b, maka;
- Jika a lebih besar dibanding b, dapat dituliskan dengan a > b
- Jika a lebih kecil dibanding b, dapat dituliskan dengan a < b
- Jika a sama dengan b, dapat dituliskan a = b.
Manakah yang lebih besar dari -4 dan 2? Tuliskan jawaban Anda dalam kolom komentar!
Klik di sini untuk pelatihan statistik Surabaya

Operasi Bilangan Bulat
Matematika jauh lebih seru dari yang Anda bayangkan jika Anda menemukan cara yang tepat untuk belajar!

Operasi hitung bilangan bulat tidak jauh berbeda dari apa yang Anda pelajari di awal, hanya saja ada beberapa aturan yang perlu Anda pahami. Operasi hitung bilangan bulat meliputi, penjumlahan, pengurangan, perkalian, serta pembagian.
Penjumlahan
Penjumlahan bilangan bulat disimbolkan dengan tanda ‘+’. Secara sederhana, penjumlahan dua bilangan bulat yang sejenis (positif atau negatif) akan menghasilkan jenis bilangan bulat yang sama. Pahami contoh berikut ini:
1 + 5 = 6
-2 + (-8) = -10
Sementara, penjumlahan bilangan bulat berbeda jenis hasilnya merupakan pengurangan dan jenisnya ditentukan dengan jenis bilangan yang terbesar. Perhatikan contoh berikut ini:
7 + (-2) = 5
-6 + 5 = -1
Dalam penjumlahan bilangan bulat berlaku sifat asosiatif, komutatif, dan unsur identitas.
Pengurangan
Pengurangan bilangan bulat disimbolkan dengan tanda ‘-‘. Aturan khusus pada operasi pengurangan adalah suatu bilangan dikurangi dengan bilangan negatif maka operasinya berubah menjadi penjumlahan. Simak contoh berikut:
4 - 2 = 2
3 – 7 = -4
3 – (-2) = 3 + 2 = 5
Perkalian
Perkalian bilangan bulat disimbolkan dengan tanda ‘x’. Perkalian bilangan bulat berlaku sifat asosiatif, komutatif, dan distributif. Terdapat aturan khusus pada operasi perkalian bilangan bulat:
- Bilangan asli dikalikan dengan bilangan asli hasilnya bilangan asli. Contoh 1 x 3 = 3
- Bilangan bulat negatif dikalikan dengan bilangan bulat negatif hasilnya bilangan bulat positif. Contoh : -2 x (-4) = 8
- Bilangan asli dikalikan dengan bilangan bulat negatif hasilnya bilangan bulat negatif. Contoh 3 x (-2) = -6
Pembagian
Pembagian bilangan bulat disimbolkan dengan “”. Aturan khusus pada operasi pembagian sama dengan perkalian, namun tidak berlaku sifat komutatif, asosiatif, dan jika dibagi dengan nol menghasilkan nilai tidak terdefinisi.
Bilangan bulat termasuk subjek matematika yang mudah dipahami bukan? Jika Anda merasa membutuhkan pendampingan untuk belajar matematika, Superprof menawarkan kursus privat matematika terbaik untuk Anda.
Cara Mengurutkan Bilangan Bulat
Mengurutkan bilangan bulat berarti menyusun angka-angka tersebut dari nilai yang paling kecil ke yang terbesar, atau sebaliknya. Pada garis bilangan, posisi semakin ke kanan menunjukkan nilai yang lebih besar, sedangkan semakin ke kiri menandakan nilai yang lebih kecil.
Hal ini juga berlaku pada bilangan negatif—semakin besar angkanya secara bentuk (misalnya -1, -2, -10), justru nilainya semakin kecil. Sebaliknya, untuk bilangan positif, angka yang lebih besar menunjukkan nilai yang lebih tinggi pula.
Contoh Soal Bilangan Bulat Positif dan Negatif Kelas 6
Soal 1 – Penjumlahan dan Pengurangan
- Hitung: 7+(−3)=…7 + (-3) = …7+(−3)=…
- Hitung: −5+8=…-5 + 8 = …−5+8=…
- Hitung: −10−4=…-10 - 4 = …−10−4=…
- Hitung: 6−(−2)=…6 - (-2) = …6−(−2)=…
Jawaban:
- 7+(−3)=47 + (-3) = 47+(−3)=4
- −5+8=3-5 + 8 = 3−5+8=3
- −10−4=−14-10 - 4 = -14−10−4=−14
- 6−(−2)=86 - (-2) = 86−(−2)=8
Soal 2 – Perbandingan Bilangan Bulat
- Manakah yang lebih besar: –7 atau –3?
- Urutkan bilangan berikut dari yang terkecil hingga terbesar: –5, 3, 0, –2, 4
Jawaban:
- –3 lebih besar daripada –7
- Urutan dari kecil ke besar: –5, –2, 0, 3, 4
Soal 3 – Penerapan dalam Kehidupan Sehari-hari
- Suhu di kota A = –4°C, suhu di kota B = 3°C. Kota manakah yang lebih dingin?
- Seorang anak berada di lantai -2 gedung parkir, lalu naik ke lantai 3. Berapa lantai yang dilalui anak tersebut?
Jawaban:
- Kota A lebih dingin karena –4°C < 3°C
- Selisih lantai = 3 – (–2) = 5 lantai
Garis Bilangan Bulat
Garis bilangan bulat adalah garis lurus yang digunakan untuk menampilkan posisi bilangan bulat secara berurutan dari yang terkecil hingga yang terbesar. Garis ini membantu siswa memahami konsep bilangan positif, nol, dan bilangan negatif secara visual. Misalnya, angka 0 berada di tengah, bilangan positif seperti 1, 2, 3 berada di sisi kanan, sedangkan bilangan negatif seperti –1, –2, –3 berada di sisi kiri.
Dengan garis bilangan bulat, kita juga dapat dengan mudah melakukan operasi penjumlahan, pengurangan, dan membandingkan bilangan bulat. Misalnya, untuk menghitung 2+(−3)2 + (-3), kita cukup bergerak 2 langkah ke kanan dari nol, kemudian 3 langkah ke kiri, sehingga hasilnya –1. Garis bilangan bulat juga membantu mengaitkan konsep bilangan dengan kuadran 1 2 3 4 dalam bidang koordinat kartesius, sehingga siswa dapat memahami bilangan dalam konteks dua dimensi maupun satu dimensi.
Garis Bilangan dan Kuadran
Selain digunakan pada garis bilangan, konsep posisi bilangan juga dapat dikaitkan dengan sistem koordinat kartesius yang terdiri dari kuadran 1 2 3 4. Dalam sistem ini, bilangan bulat positif biasanya muncul pada Kuadran I, yang memuat nilai x dan y positif. Kuadran II memuat bilangan bulat negatif pada sumbu x dan positif pada sumbu y.
Pada Kuadran III, kedua nilai x dan y bernilai negatif, sedangkan Kuadran IV memuat x positif dan y negatif. Pemahaman mengenai kuadran 1 2 3 4 membantu memperluas konsep contoh bilangan bulat dalam konteks bidang datar, bukan hanya pada garis bilangan satu dimensi.
Penerapan Bilangan Bulat
Bilangan bulat memiliki banyak kegunaan dalam berbagai bidang dan aktivitas sehari-hari, di antaranya:
- Matematika: Digunakan dalam operasi dasar seperti penjumlahan, pengurangan, perkalian, hingga pembagian menggunakan nilai-nilai utuh.
- Ilmu Komputer: Dipakai dalam pemrograman, misalnya untuk perhitungan logika, penanda indeks pada array, dan berbagai fungsi lainnya.
- Ekonomi: Dimanfaatkan dalam pencatatan data keuangan, termasuk menghitung jumlah produk, transaksi, atau nilai uang tertentu.
- Fisika: Diterapkan untuk menyatakan besaran seperti suhu, kecepatan, atau waktu ketika diukur menggunakan nilai satuan tanpa pecahan.
Jangan lewatkan artikel kami tentang Diagram Venn berikut.
Ringkaskan dengan AI