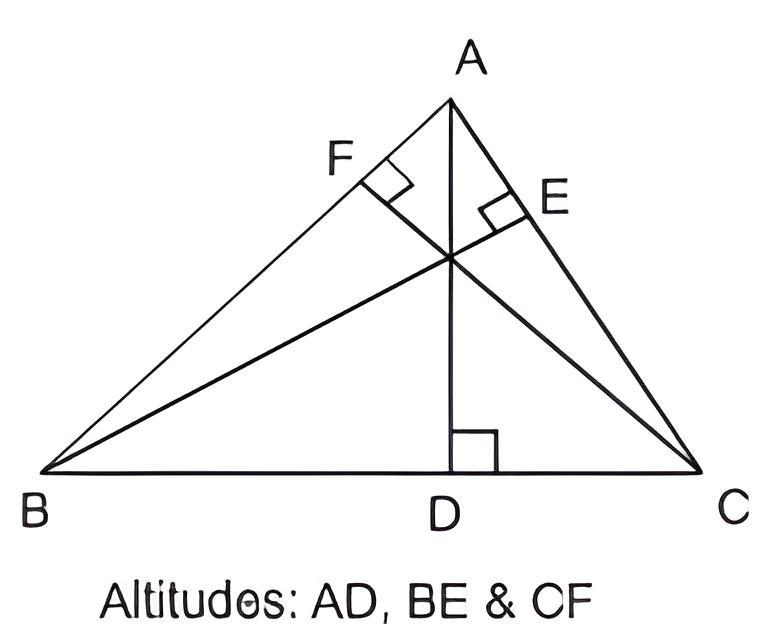
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut dalam segitiga. Dalam kehidupan sehari-hari, trigonometri digunakan dalam berbagai bidang seperti astronomi, navigasi, arsitektur, dan masih banyak lagi. Pada artikel ini, kita akan membahas berbagai konsep dasar trigonometri, termasuk rumus sin cos tan, serta aturan sinus dan cosinus yang sangat penting dalam trigonometri kelas 10. Kita juga akan menguraikan rumus trigonometri lengkap yang sering digunakan dalam memecahkan berbagai masalah.

Pengertian Trigonometri
Trigonometri adalah studi tentang hubungan antara sudut dan panjang sisi dalam segitiga. Nama "trigonometri" berasal dari bahasa Yunani: "trigonon" (segitiga) dan "metron" (pengukuran). Pada dasarnya, trigonometri membantu kita memahami dan menghitung panjang sisi atau besar sudut dalam segitiga ketika beberapa informasi diberikan.
Anda bisa menemukan les olimpiade matematika sekarang!
Jenis-Jenis Perbandingan Trigonometri
Dalam trigonometri, terdapat tiga perbandingan dasar yang sangat penting untuk dipahami yaitu sinus (sin), kosinus (cos), dan tangen (tan). Perbandingan-perbandingan ini menggambarkan hubungan antara sisi-sisi dan sudut dalam sebuah segitiga siku-siku. Berikut ini adalah penjelasan mendetail mengenai masing-masing perbandingan trigonometri:
Sinus (sin)
Sinus adalah perbandingan antara panjang sisi di depan sudut dan panjang sisi miring dalam sebuah segitiga siku-siku. Notasi sinus biasanya ditulis sebagai sin. Rumus untuk mencari nilai sinus suatu sudut adalah:

Pelajari juga tentang bagaimana mencari dan menentukan fungsi invers dalam matematika!
Contoh:
Panjang sisi di depan sudut (opposite) adalah 3 cm, dan panjang sisi miring (hypotenuse) adalah 5 cm. Maka nilainya adalah:
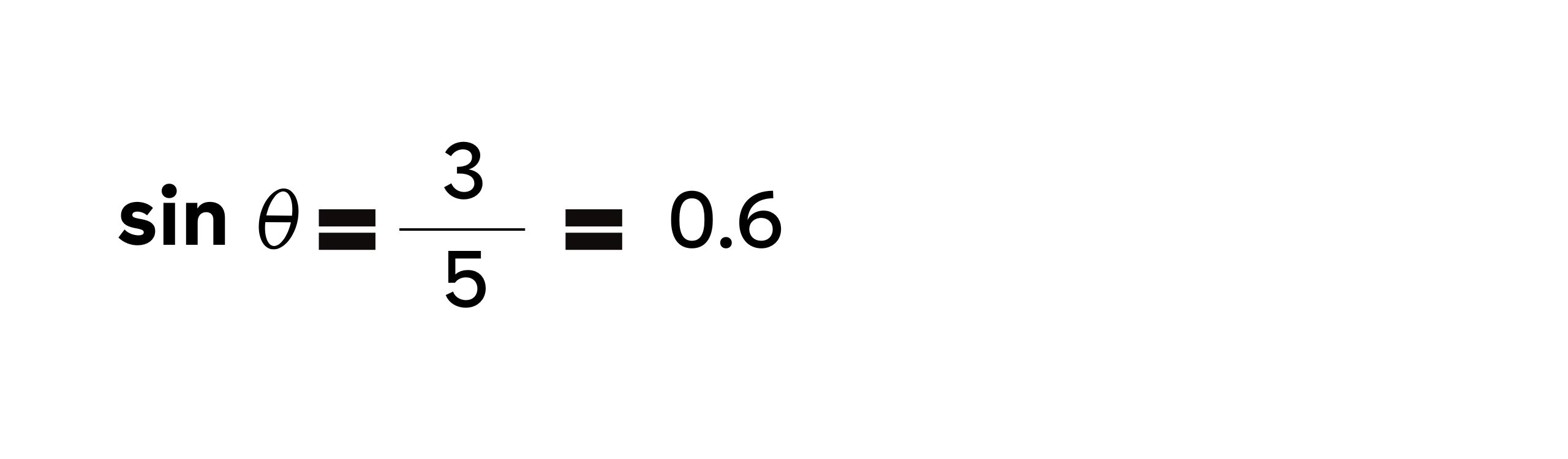
Kosinus (cos)
Kosinus adalah perbandingan antara panjang sisi yang bersebelahan dengan sudut dan panjang sisi miring dalam sebuah segitiga siku-siku. Notasi kosinus biasanya ditulis sebagai cos. Rumus cos suatu sudut adalah:

Contoh:
Panjang sisi yang bersebelahan dengan sudut (adjacent) adalah 4 cm, dan panjang sisi miring (hypotenuse) adalah 5 cm. Maka nilainya adalah:
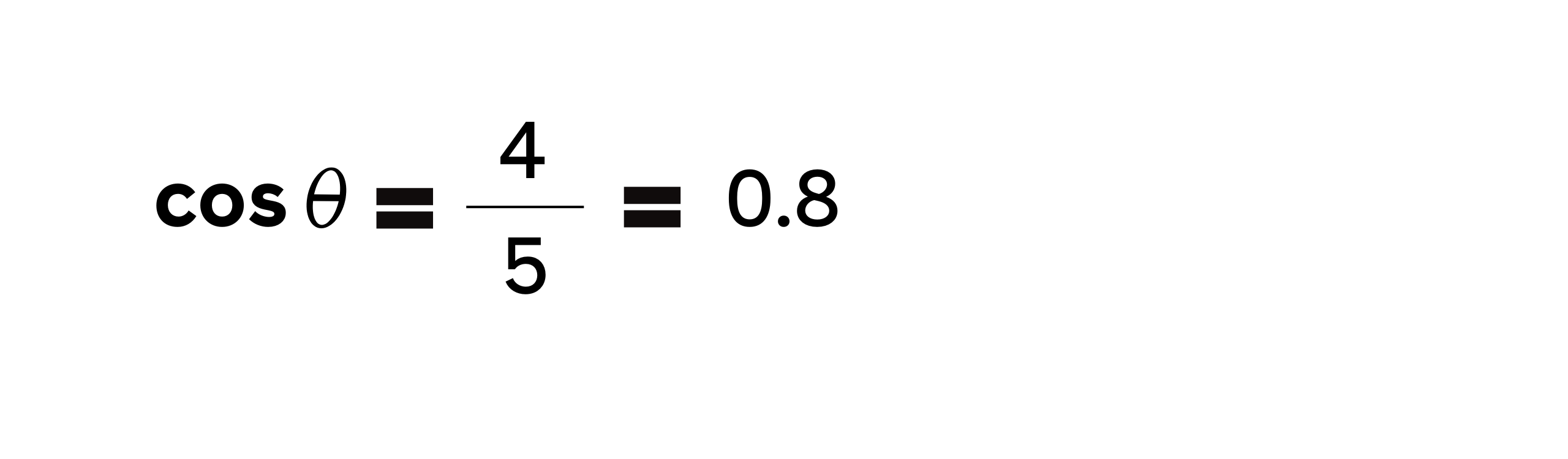
Tangen (tan)
Tangen adalah perbandingan antara panjang sisi di depan sudut dan panjang sisi yang bersebelahan dengan sudut dalam sebuah segitiga siku-siku. Notasi tangen biasanya ditulis sebagai tan. Rumus untuk mencari nilai tangen suatu sudut adalah:

Jangan lewatkan artikel lain yang menjelaskan tentang matriks matematika!
Contoh:
Panjang sisi di depan sudut (opposite) adalah 3 cm, dan panjang sisi yang bersebelahan dengan sudut (adjacent) adalah 4 cm. Maka nilainya adalah:
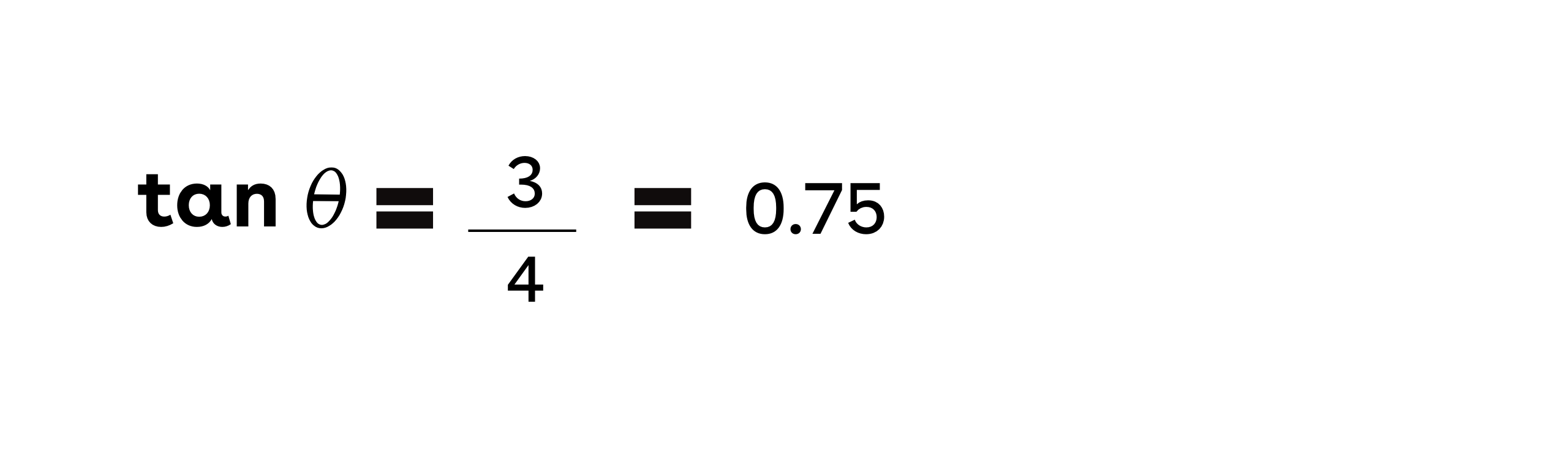
Temukan les matematika di medan
Hubungan Antara Sinus, Kosinus, dan Tangen
Sinus, kosinus, dan tangen tidak hanya digunakan secara terpisah tetapi juga memiliki hubungan erat satu sama lain dalam trigonometri. Berikut adalah beberapa identitas trigonometri yang menunjukkan hubungan ini:
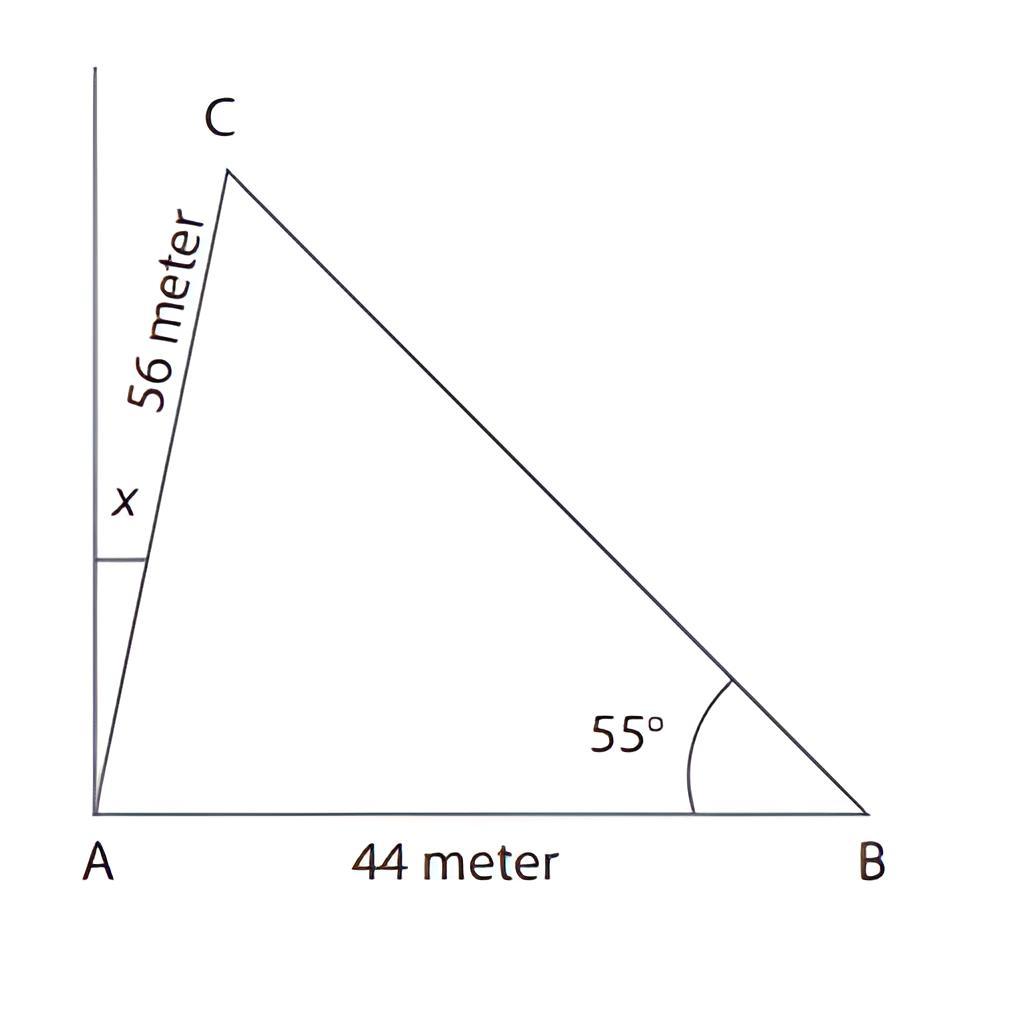
- Identitas Pythagoras:
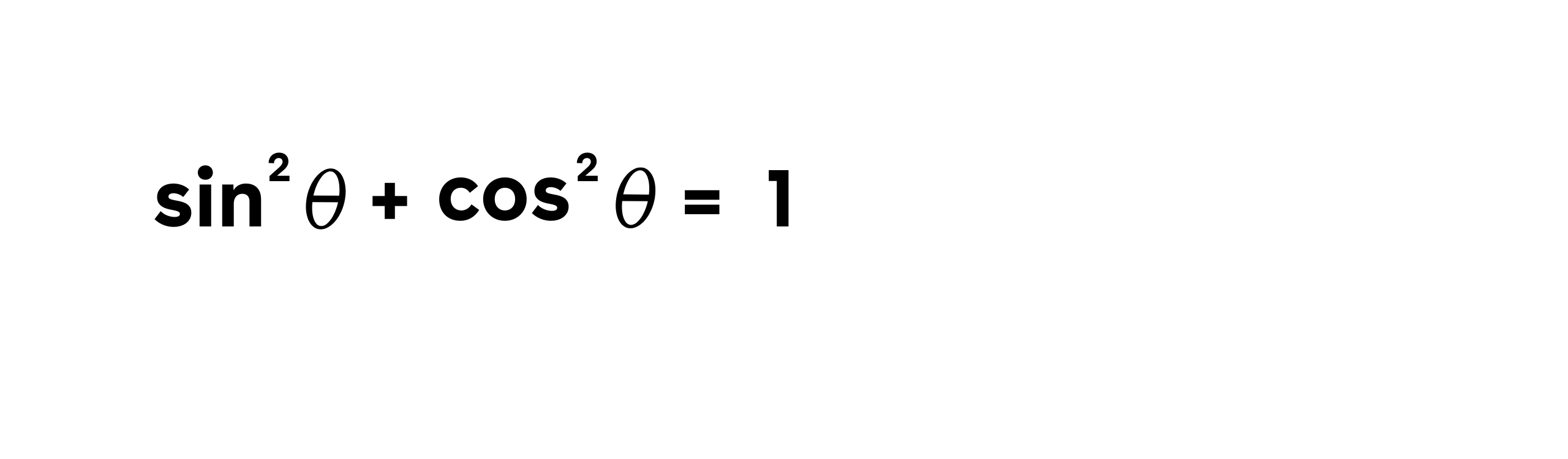
Identitas ini berasal dari Teorema Pythagoras dan berlaku untuk setiap sudut ᶿ.
- Hubungan Tangen dengan Sinus dan Kosinus:
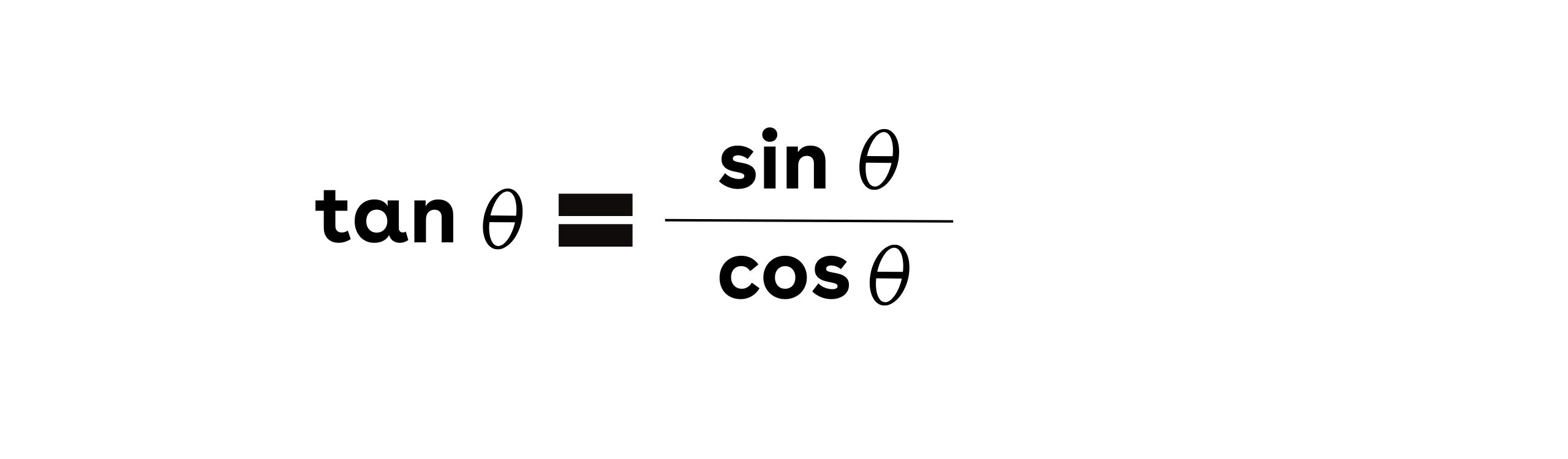
Identitas ini menunjukkan bahwa tangen suatu sudut adalah perbandingan antara sinus dan kosinus sudut tersebut.
- Hubungan Sekan (sec), Kosekan (csc), dan Kotangen (cot):
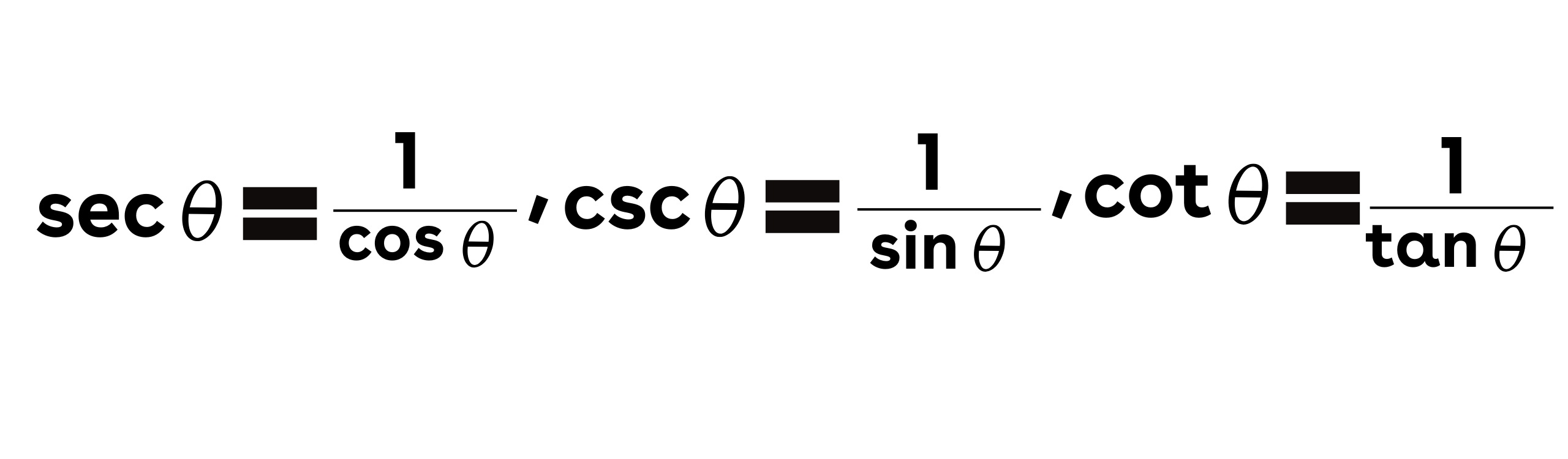
Sekan (sec), kosekan (csc), dan kotangen (cot) adalah kebalikan dari kosinus, sinus, dan tangen, masing-masing.
Pelajari juga bagaimana menghitung rumus peluang!

Aturan Sinus
Aturan sinus adalah salah satu rumus trigonometri lengkap yang sangat berguna dalam memecahkan masalah yang melibatkan segitiga sembarang. Aturan ini menyatakan bahwa perbandingan antara panjang sisi segitiga dengan sinus sudut yang berhadapan dengannya adalah konstan.
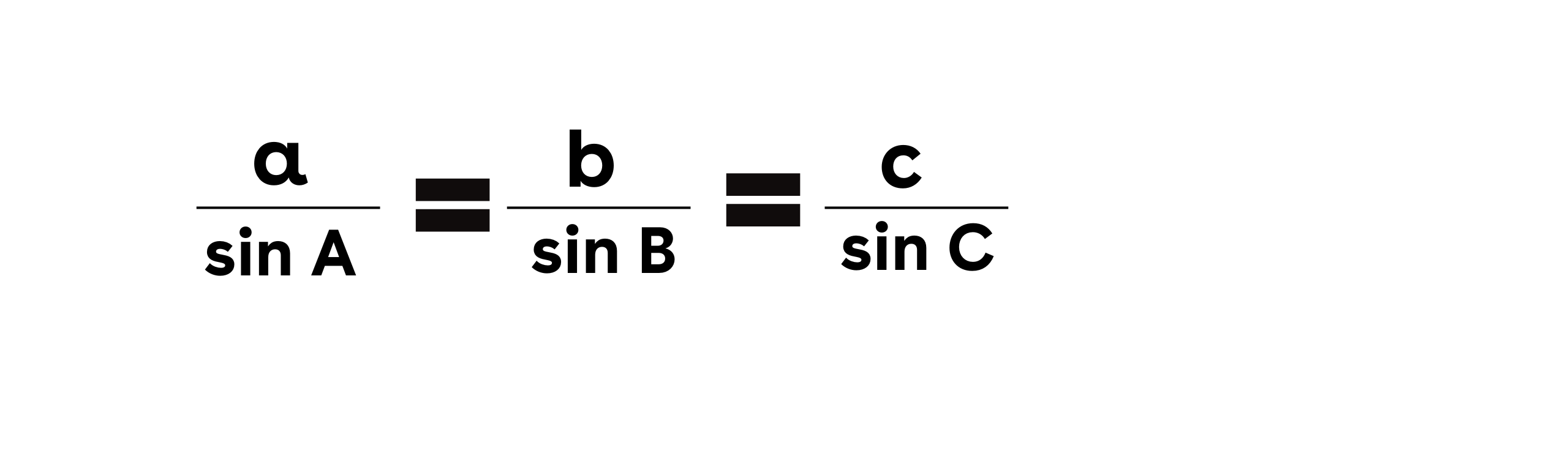
Di sini, a , b, dan c adalah panjang sisi-sisi segitiga, dan A, B, dan C adalah sudut-sudut yang berhadapan dengan sisi-sisi tersebut. Aturan sinus dapat digunakan untuk menentukan panjang sisi atau besar sudut dalam segitiga jika dua sisi dan satu sudut yang berhadapan dengan salah satu sisi diketahui.
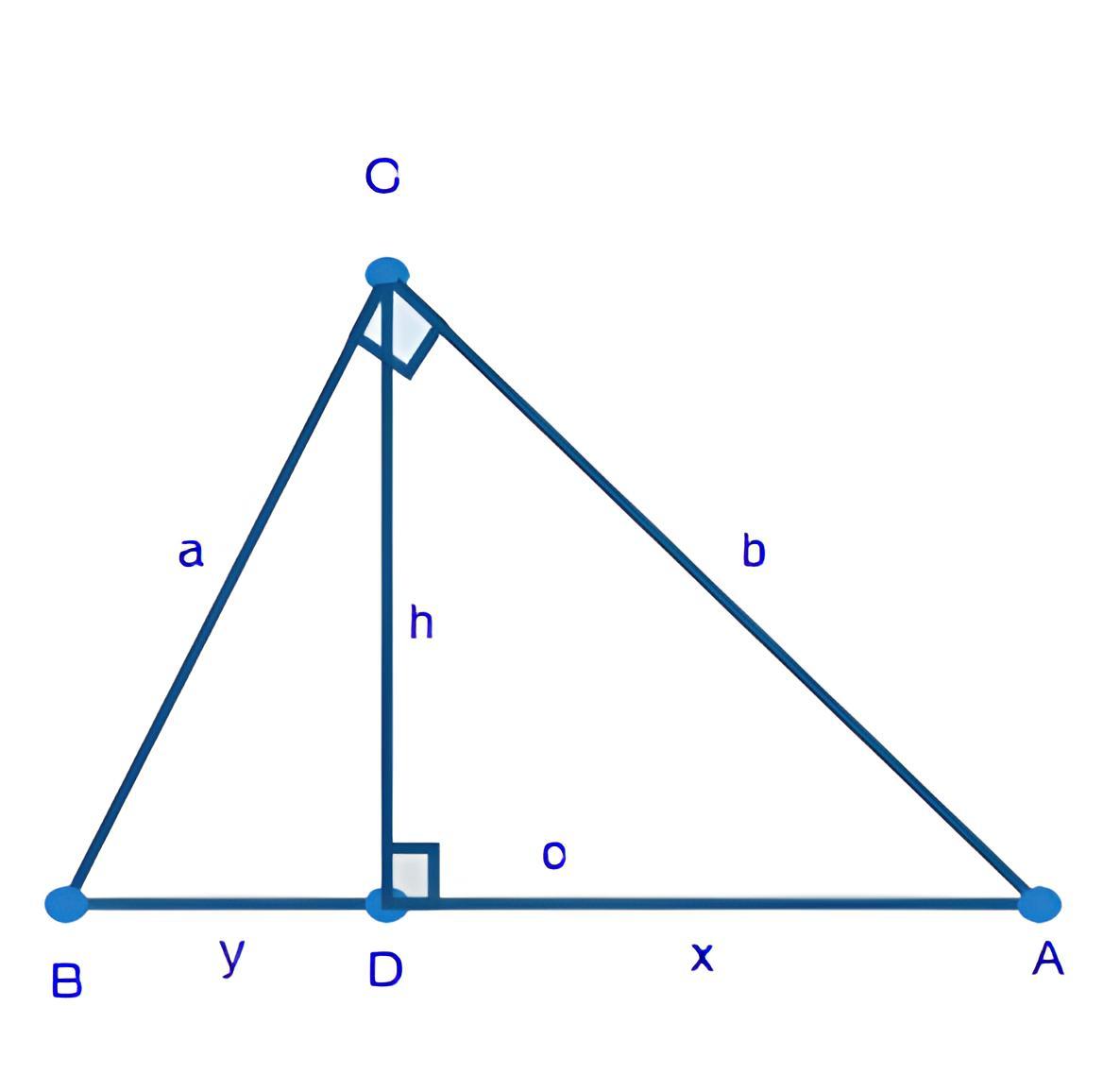
Aturan Cosinus
Aturan cosinus merupakan aturan penting lainnya dalam trigonometri. Aturan ini digunakan untuk menghitung panjang sisi atau besar sudut dalam segitiga jika dua sisi dan sudut apitnya diketahui. Aturan ini juga berguna ketika kita mengetahui ketiga sisi segitiga dan ingin menemukan salah satu sudutnya.
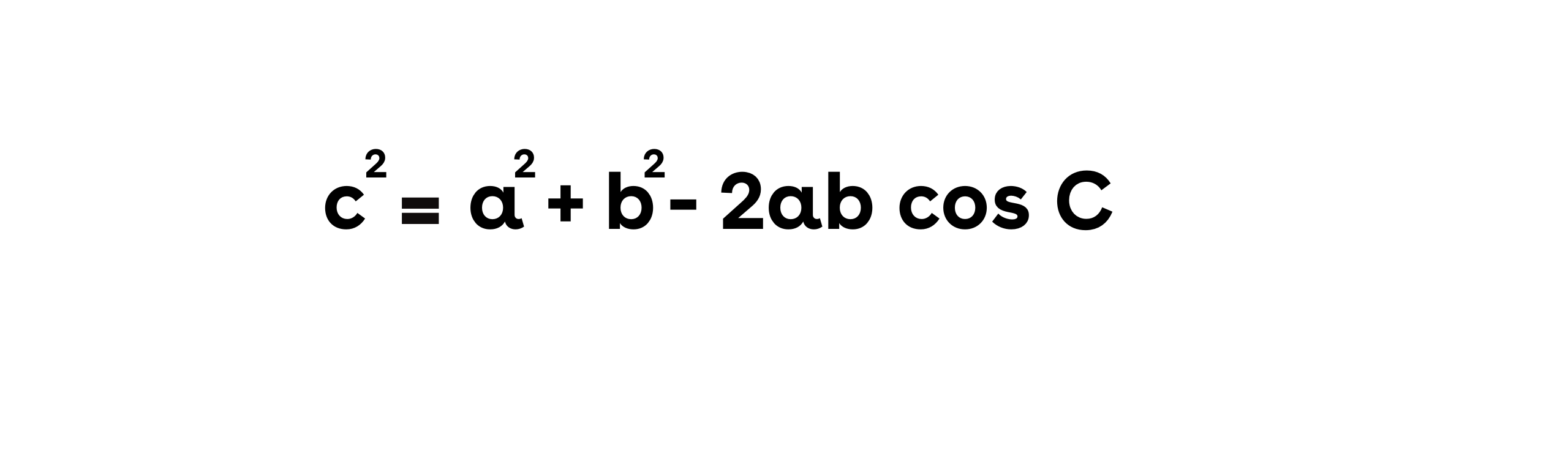
Aturan cosinus dapat dinyatakan untuk ketiga sisi sebagai berikut:
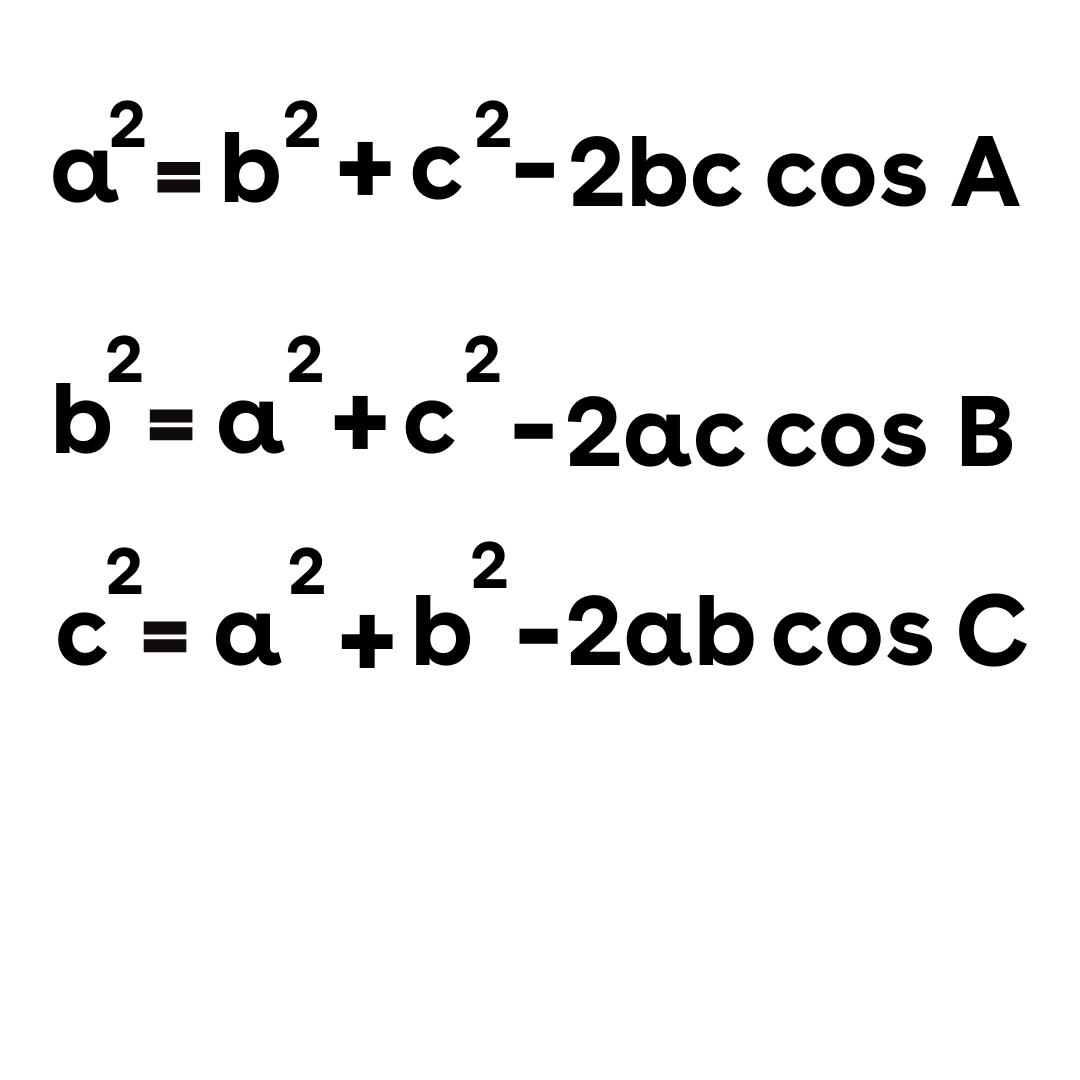
Ternyata semudah ini cara mencari persamaan lingkaran.
Penerapan Aturan Sinus dan Cosinus dalam Kehidupan Sehari-hari
Baik aturan sinus maupun cosinus memiliki banyak aplikasi praktis dalam kehidupan sehari-hari dan berbagai bidang ilmu pengetahuan. Contohnya, dalam arsitektur dan teknik sipil, trigonometri digunakan untuk menghitung panjang sisi bangunan atau jembatan yang kompleks. Dalam astronomi, trigonometri membantu dalam menghitung jarak antara bintang-bintang atau planet. Di bidang navigasi, trigonometri digunakan untuk menentukan posisi kapal atau pesawat di peta.
Contoh Soal Trigonometri Kelas 10
Untuk membantu memperdalam pemahaman Anda tentang trigonometri, berikut adalah beberapa contoh soal yang sering muncul di trigonometri kelas 10 beserta pembahasannya.
Contoh Soal 1
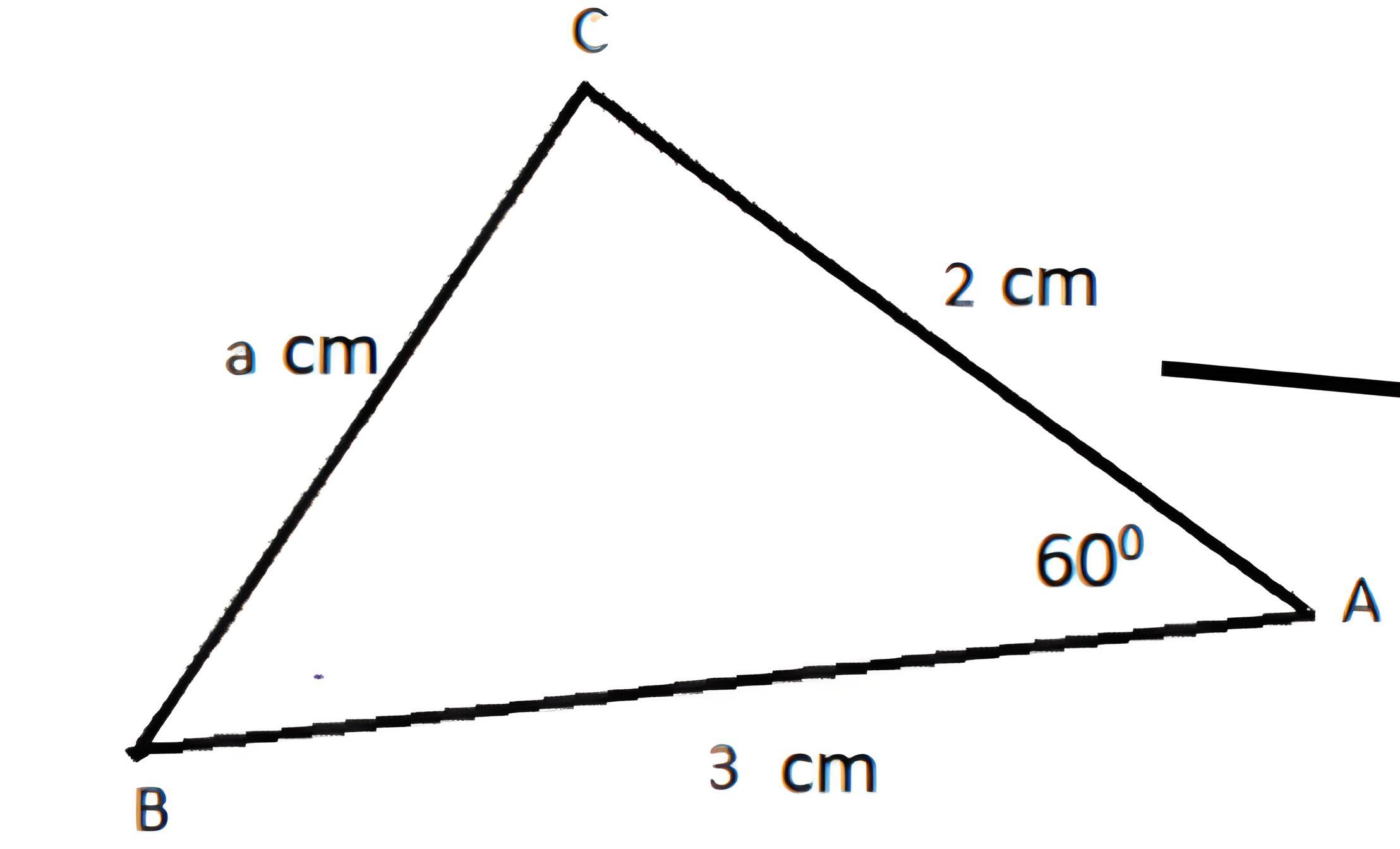
Sebuah segitiga ABC memiliki sudut A = 30º, sisi a = 3 cm, dan sisi b = 4 cm. Tentukan besar sudut B, sudut C, dan panjang sisi c!
Pembahasan:
Menggunakan aturan sinus:
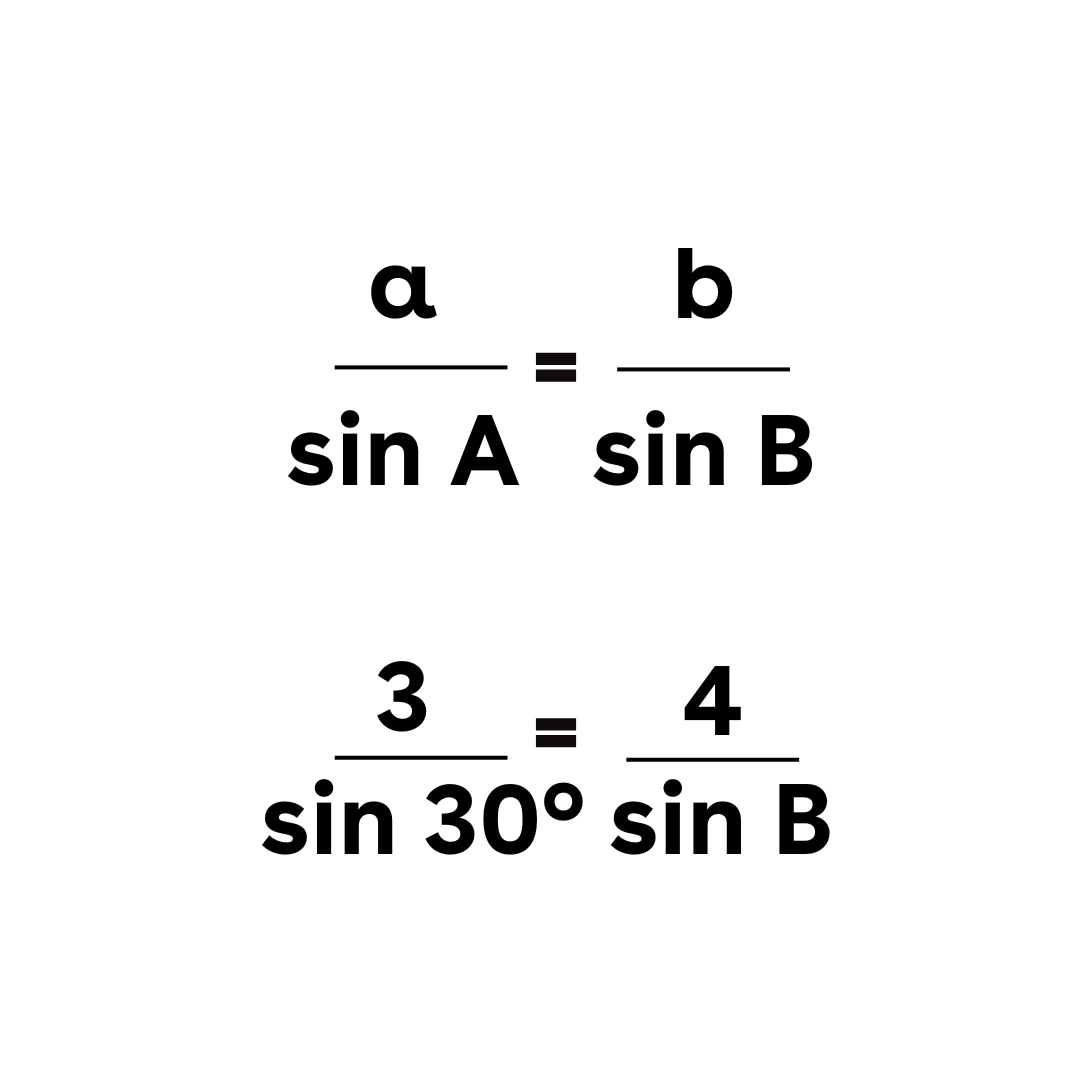
Karena sin 30º = 0.5:
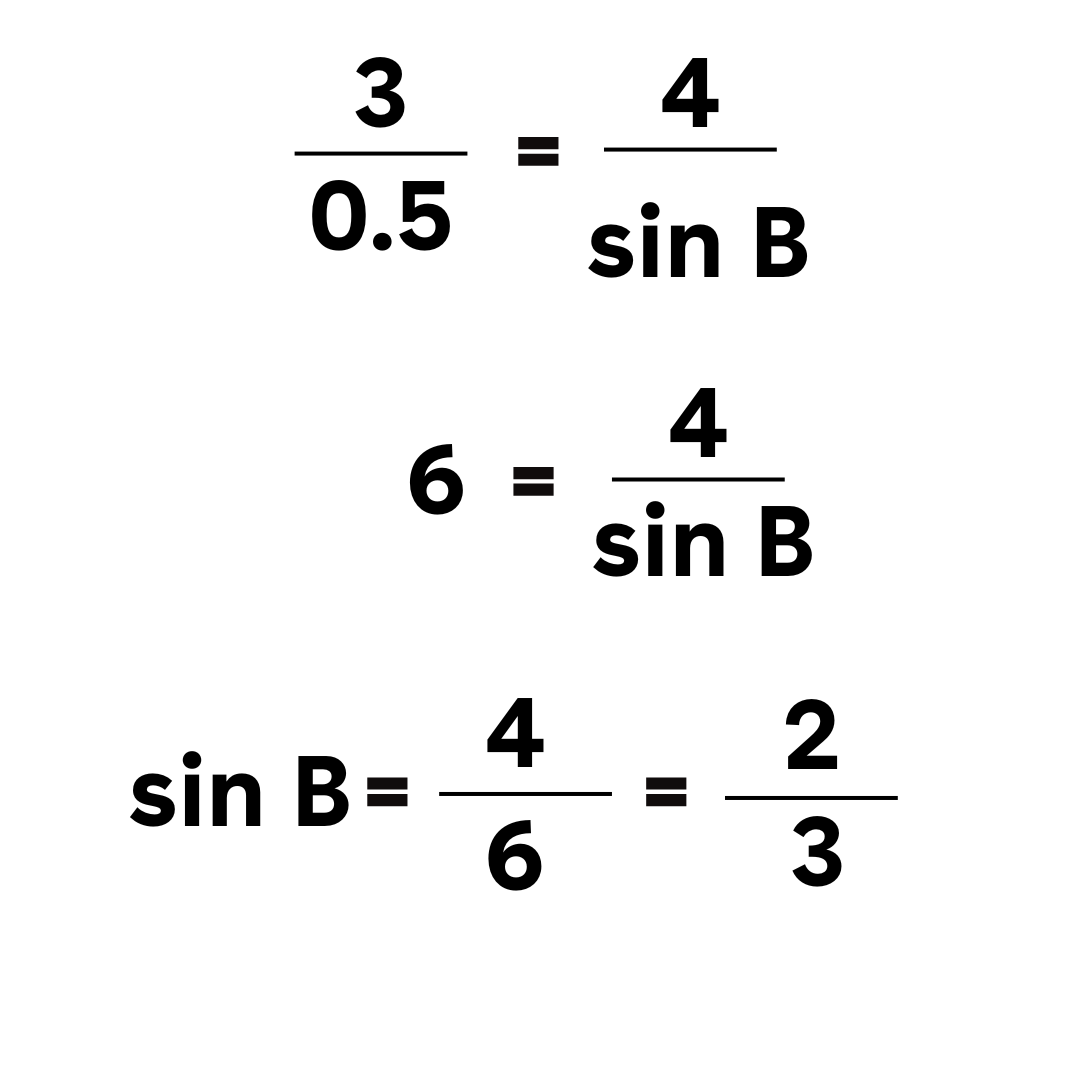
Dengan menggunakan kalkulator atau tabel trigonometri, kita dapat menemukan bahwa:

Untuk sudut C, kita menggunakan jumlah sudut dalam segitiga:
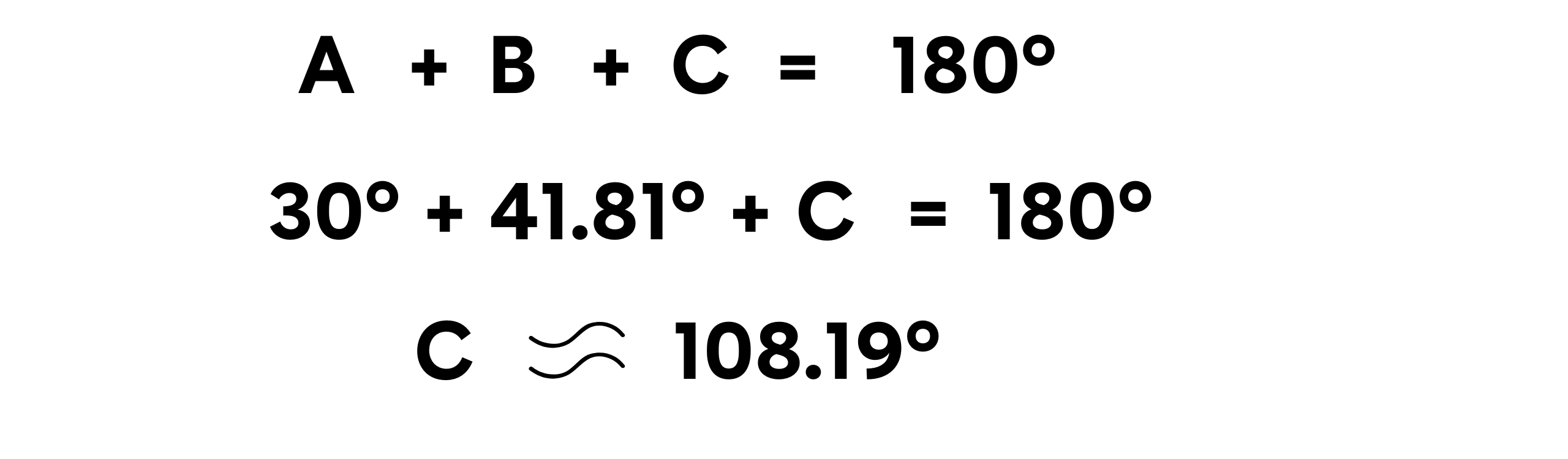
Untuk panjang sisi c, kita menggunakan aturan sinus lagi:
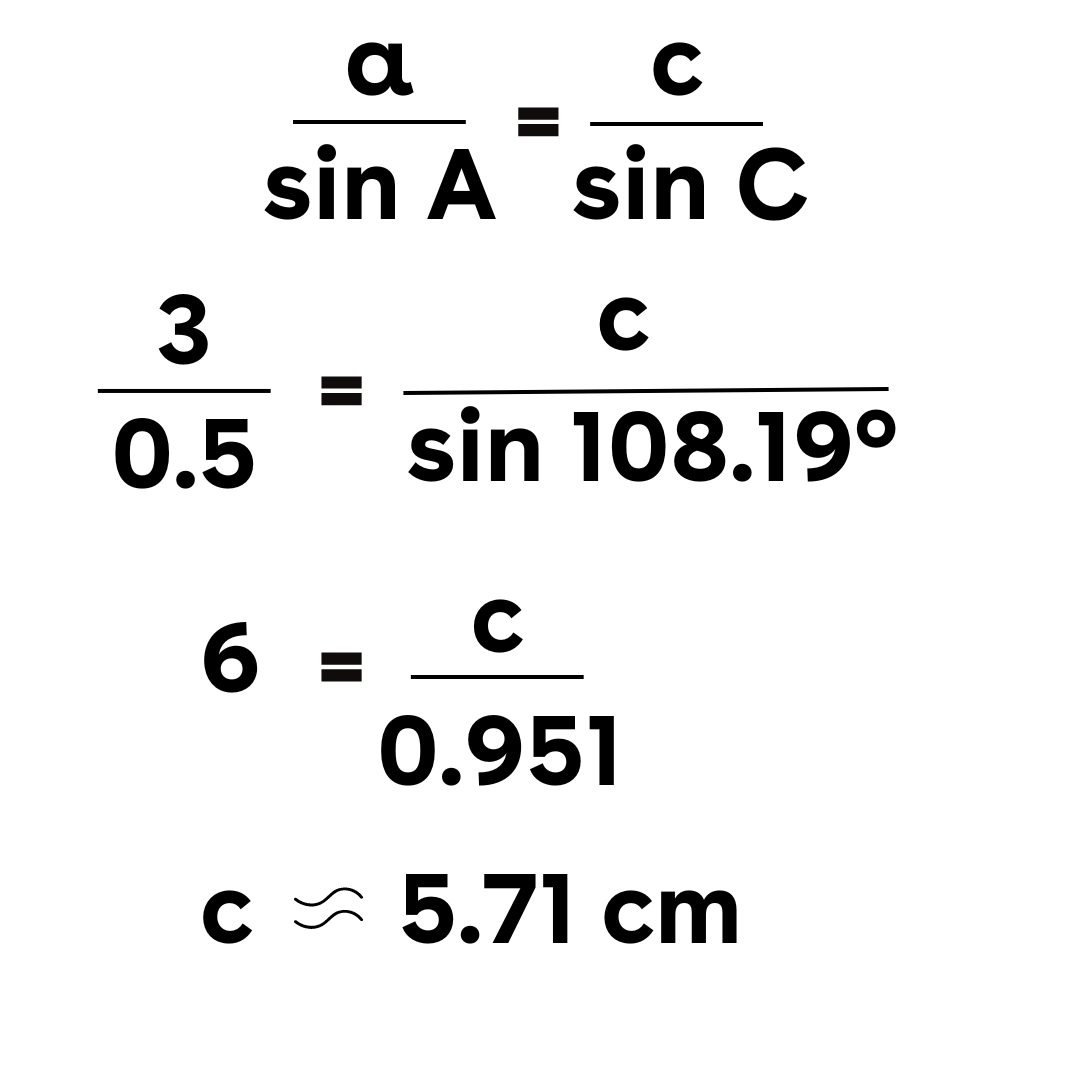
Contoh Soal 2
Diketahui segitiga ABC dengan panjang sisi a = 5 cm, panjang sisi c = 6 cm, dan besar sudut B = 60º. Tentukan panjang sisi b!
Pembahasan:
Menggunakan aturan cosinus:
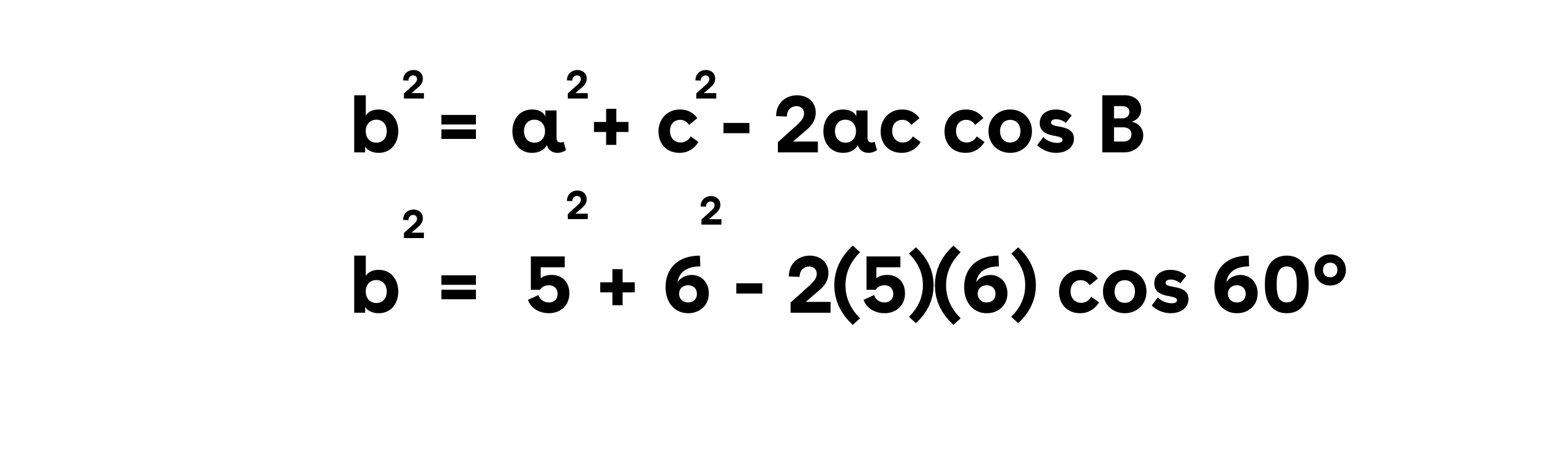
Karena cos 60º = 0.5:
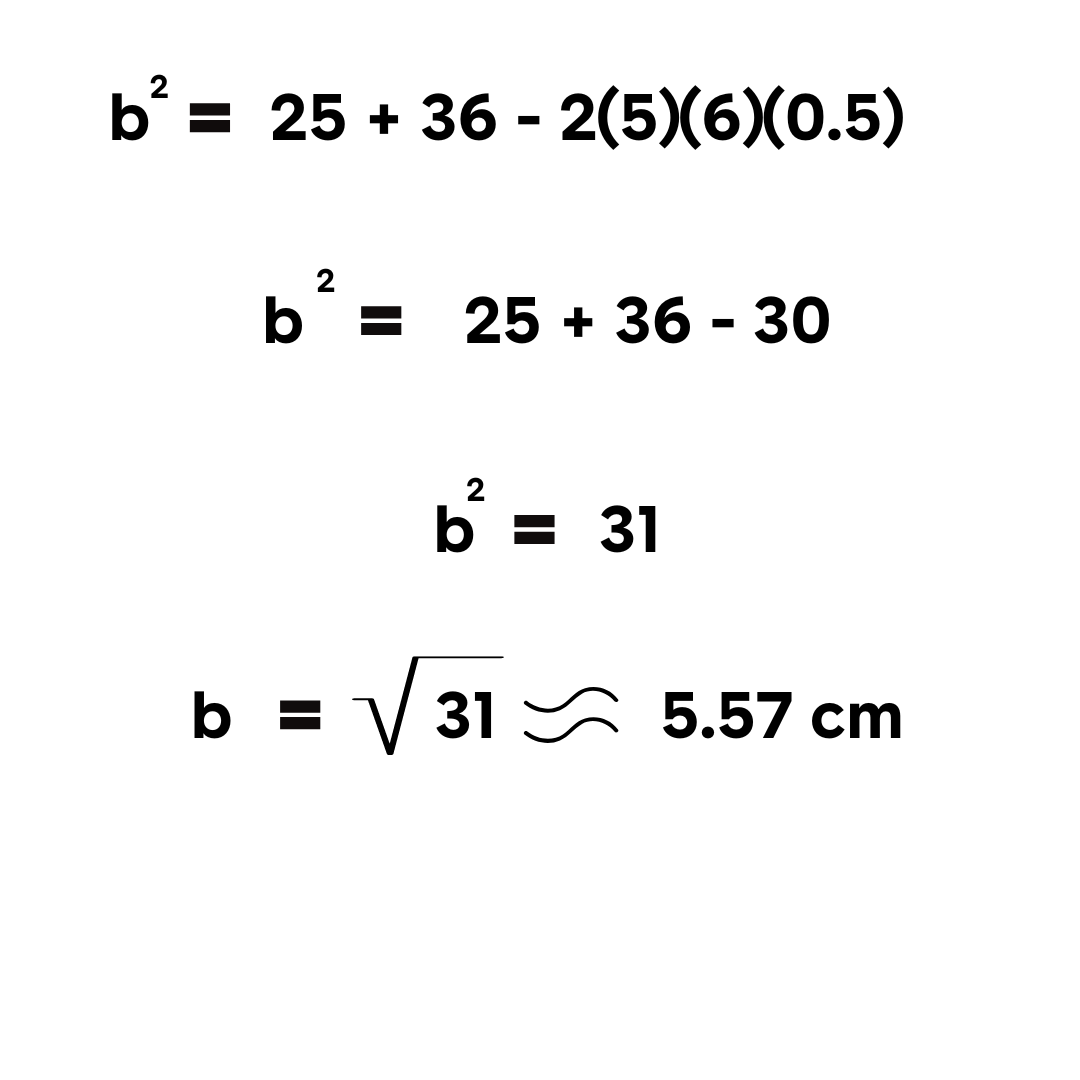
Contoh Soal 3
Diketahui sebuah segitiga dengan sisi-sisi a = 7 cm, b = 8 cm, dan c = 10 cm. Tentukan besar sudut terbesar dalam segitiga tersebut!
Pembahasan:
Sudut terbesar akan berhadapan dengan sisi terpanjang, yaitu c = 10 cm. Menggunakan aturan cosinus untuk mencari sudut C:
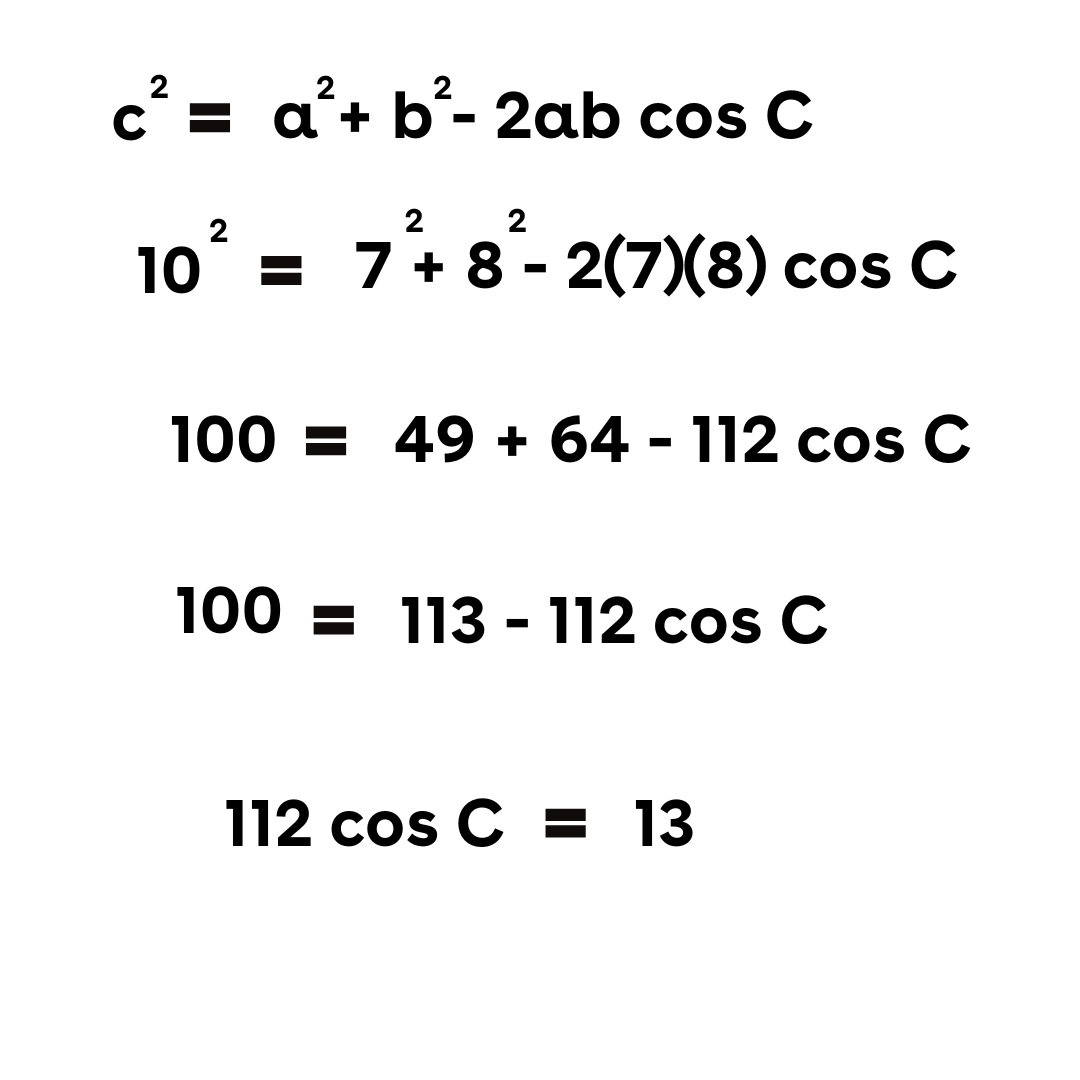
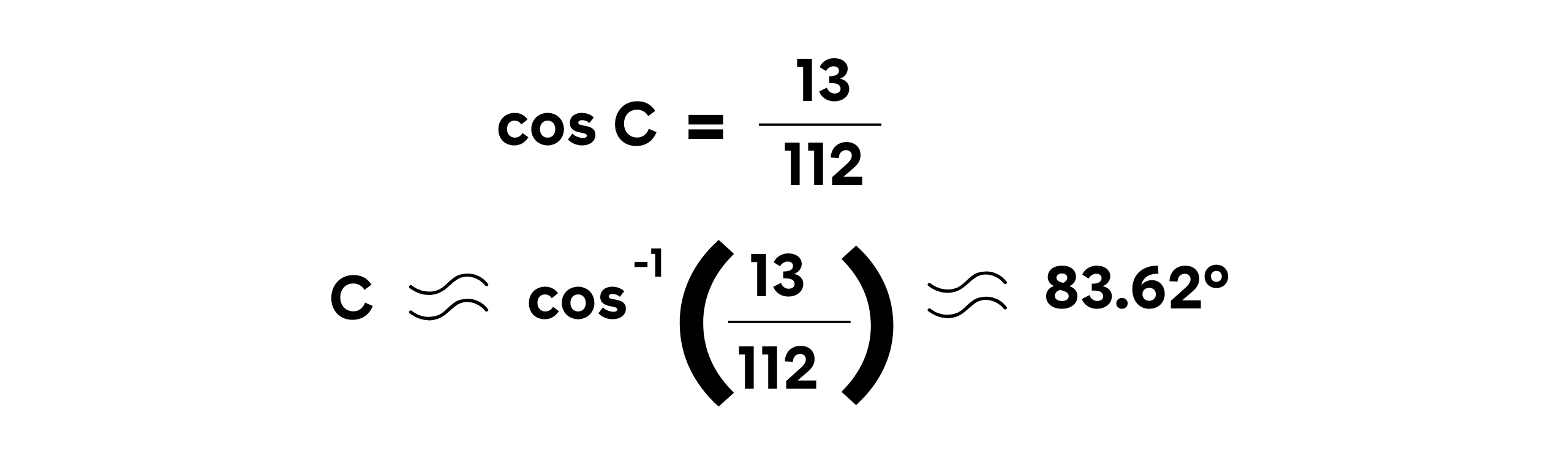
Les Privat Matematika dengan Mentor dari Superprof
Apakah Anda sedang menghadapi kesulitan dalam memahami pelajaran matematika? Tidak perlu khawatir! Superprof hadir untuk memberikan solusi terbaik bagi Anda. Kami menawarkan layanan guru privat matematika yang dapat membantu Anda untuk lebih memahami dan menguasai pelajaran matematika dengan lebih mudah dan menyenangkan.
Di Superprof, kami memahami bahwa setiap siswa memiliki cara belajar yang berbeda-beda. Oleh karena itu, kami menawarkan bimbel matematika yang disesuaikan dengan kebutuhan dan gaya belajar masing-masing siswa. Dengan les privat matematika, Anda akan mendapatkan perhatian penuh dari tutor yang berpengalaman dan profesional. Tutor kami siap membantu Anda memahami konsep-konsep sulit, menyelesaikan soal-soal kompleks, dan mempersiapkan diri untuk ujian dengan lebih percaya diri.
Mengapa memilih les privat matematika di Superprof? Berikut beberapa keuntungan yang akan Anda dapatkan:
- Tutor Berpengalaman: Kami memiliki tutor-tutor berpengalaman yang telah membantu banyak siswa meraih kesuksesan dalam pelajaran matematika. Mereka menguasai berbagai metode pengajaran yang efektif dan dapat disesuaikan dengan kebutuhan siswa.
- Pendekatan Personal: Les privat memungkinkan tutor untuk memberikan perhatian penuh kepada Anda atau anak Anda. Dengan demikian, proses belajar menjadi lebih efektif dan efisien.
- Waktu dan Tempat Fleksibel: Anda dapat memilih waktu dan tempat les yang sesuai dengan jadwal Anda. Tutor kami juga bisa datang ke rumah Anda atau mengadakan sesi secara online.
- Materi Sesuai Kebutuhan: Materi yang diajarkan disesuaikan dengan kurikulum dan kebutuhan spesifik siswa, baik itu untuk persiapan ujian, pemahaman konsep dasar, atau penanganan materi yang lebih lanjut.
Temukan tutor matematika terdekat di Superprof yang siap membantu Anda mencapai prestasi akademis yang lebih baik. Dengan tutor yang tepat, belajar matematika akan menjadi lebih menyenangkan dan menantang. Jangan biarkan matematika menjadi hambatan dalam meraih prestasi. Bergabunglah dengan ribuan siswa yang telah merasakan manfaat dari bimbingan kami.
Mulai perjalanan belajar Anda dengan langkah yang tepat. Daftar sekarang dan temukan guru privat matematika yang sesuai dengan kebutuhan Anda di Superprof. Jadikan Superprof sebagai mitra belajar Anda!
Ringkaskan dengan AI
















