Ada yang pernah naik pesawat? Apakah kalian merasakan jika pesawat lepas landas atau ketika pesawat ingin mendarat maka badan pesawat akan miring. Pesawat membutuhkan kemiringan tertentu agar bisa terbang atau bisa mendarat dengan sempurna di landasan. Kemiringan badan pesawat ini ternyata menggunakan perhitungan matematika lho. Hmmm, kira-kira perhitungan matematika apa ya yang dipakai?
Contoh yang lainnya, jika Anda perhatikan sebuah tangga, pasti Anda akan mendapati bahwa tangga dibuat secara presisi agar kemiringannya tidak membuat jarak anak tangga yang satu dengan anak tangga lainnya berbeda jarak. Jika kemiringan itu tidak diukur, bisa-bisa tangga yang dibuat dapat mencelakai penggunanya karena perbedaan jarak anak tangga yang ada.
Oleh sebab itu, dalam membuat tangga ada perhitungan matematika juga yang digunakan. Hayo, sudah bisa tebak kan? Benar, ilmu matematika yang digunakan dalam mengukur kedua hal tersebut adalah rumus gradien. Apa itu gradien? Yuk kita bahas di artikel ini.
Periksa di sini jika ingin mempelajari bilangan prima dan bilangan bulat

Definisi Gradien
Menurut Kamus Besar Bahasa Indonesia (KBBI) gradien adalah kecepatan perubahan suatu variabel dengan mengikuti koordinat ruang. Gradien merupakan angka yang menyatakan tingkat kemiringan suatu garis, jika garis tersebut semakin miring, maka semakin besar pula gradiennya. Maka jika disederhanakan pengertiannya, gradien adalah nilai yang menunjukkan kemiringan suatu garis lurus.
Lihatlah kedua gambar berikut ini :
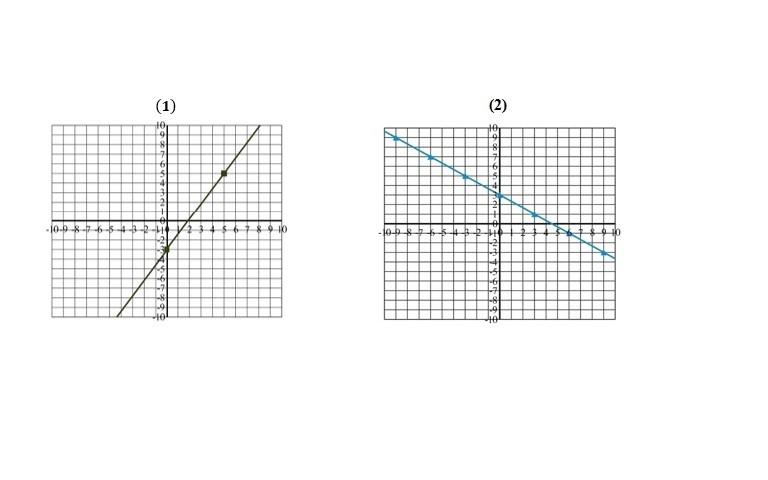
Pada gambar nomor 1 garis miringnya ke kanan sehingga diketahui jika gradiennya akan bernilai positif. Berbeda dengan gambar nomor 2 dimana garisnya miring ke kiri sehingga gradiennya akan bernilai negatif.
Dalam matematika lambang gradien adalah m dan merupakan bagian dari materi persamaan garis lurus. Amak sebelum kita lebih lanjut membahas mengenai gradien, sebaiknya Anda mengetahui rumus persamaan garis yaitu y = mx + c.
x = variable
c = konstanta
m = gradien
Maka, jika ada contoh persamaan garis y = 2x + 4, gradien dari garis tersebut adalah 2.
Cek di sini jika sedang mencari les matematika terbaik
Sifat-Sifat Gradien
Sebelum ke rumus mencari gradien, Anda perlu mengetahui sifat-sifat gradien. Ini akan membantu Anda lebih memahami apa yang dimaksud dengan gradien garis.
- Gradien dapat bernilai positif atau negatif.
- Gradien garis horizontal adalah nol.
- Gradien garis vertikal adalah tidak terdefinisi.
- Gradien garis menanjak adalah positif.
- Gradien garis menurun adalah negatif.
- Dua garis sejajar memiliki gradien yang sama.
- Hasil kali gradien kedua garis tegak lurus adalah -1.
Jika Anda merasa membutuhkan tutor untuk mengajari Anda mengenai gradien, maka Anda bisa membuka website Superprof.
Lalu Anda bisa cek di sini juga jika ingin mempelajari lebih dalam tentang pengertian kubus.

Rumus Gradien dan Contoh Soal
Segala sesuatu yang ada di matematika tak terelakkan oleh rumus, begitu juga gradien. Cara mencari gradien bisa menggunakan rumus gradien. Ada dua cara jika ingin mencari nilai gradien sebagai berikut :
- Jika Diketahui Bentuk Persamaan Garisnya
Bentuk persamaan garis lurus ada dua macam yaitu :
- y = mx + c
- ax + by + c = 0
Mari kita mencoba mencari nilai gradien garis lurus dengan menggunakan persamaan garis y = mx + c. Pada persamaan garis ini mencari gradien sangatlah mudah sebab gradiennya adalah koefisien dari variabel x sendiri yaitu m.
Contoh : Garis y = 2x + 5, koefisien x adalah 2, maka gradien garis tersebut adalah 2.
Mari kita mencoba mencari nilai gradien garis lurus dengan menggunakan persamaan garis ax + by + c = 0. Pertama-tama mari kita ubah dulu persamaan garis tersebut ke bentuk y = mx + c. Agar lebih paham, yuk kerjakan soal berikut :
Soal : hitunglah gradien pada persamaan garis berikut 4x + 3y – 6 = 0!
Pembahasan :
Kita ubah dulu persamaan 4x + 3y – 6 = 0 ke bentuk y = mx + c
4x + 3y – 6 = 0
3y = -4x + 6
Koefisien x bernilai positif, yaitu 4, sehingga setelah kita pindah ruas ke kanan akan bernilai negatif. Begitu juga dengan konstanta -6 yang berubah tanda menjadi 6 karena pindah ruas ke kanan. Selanjutnya, kita bagi kedua ruas dengan 3.
y = (-4/3)x + 8
Jadi, gradien dari persamaan garis tersebut adalah -4/3.
- Jika Diketahui Dua Titik yang Dilalui Garis
Jika ada dua titik yang dilalui suatu garis lurus, maka rumus gradien garis adalah m = m = (y2-y1) / (x2-x1). Yuk kita langsung ke contoh soal, perhatikan gambar berikut! Berapa gradien garis k?
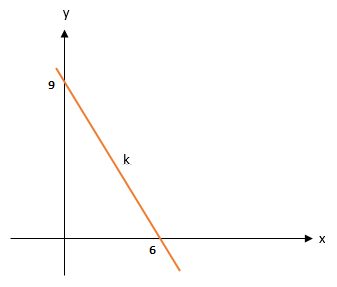
Pembahasan :
Dua buah titik yang dilalui oleh garis k yaitu (6,0) dan (0,9). Semisal (x1,y1) = (6,0) dan (x2,y2) = (0,9), gradien garis tersebut dapat dicari dengan menggunakan rumus m = (y2-y1) / (x2-x1).
m = (9-0) / (0-6)
m = 9/-6
m = -3/2
Maka, gradien garis tersebut adalah -3/2
Sesuai dengan sifat gradien, jika garis miring ke kiri atau menurun maka hasil gradiennya akan bernilai negatif.
Mudahkan menghitung nilai gradien? Asalkan Anda mengetahui sifat-sifat dan rumus mencari nilai gradien tersebut. Les privat matematika bisa membantu Anda lebih memahami pelajaran-pelajaran matematika selanjutnya. Seperi memahami sudut dalam matematika. Temukan guru matematika berkompeten hanya di Superprof!
Ringkaskan dengan AI
















