Menyelesaikan soal-soal matematika lebih banyak membutuhkan logika. Coba bantu Renald menyelesaikan permasalahan matematika berikut.
Renald diberi tugas oleh wali kelasnya untuk mendata mata pelajaran apa saja yang sudah dikuasai oleh 40 siswa temannya di kelas sebagai bahan evaluasi persiapan Ujian Tengah Semester. Mata pelajaran yang menjadi fokus Renald untuk bahan survei adalah IPA dan IPS. Dari hasil survei didapatkan, 23 siswa menguasai IPA, 15 siswa menguasai IPS, dan 8 siswa menguasai kedua mata pelajaran tersebut. Sementara, ada juga 10 siswa yang belum menguasai mata pelajaran IPA dan IPS.
Jika dijumlahkan kembali, keseluruhan siswanya menjadi 56 siswa. Jumlah itu tidak sama dengan jumlah siswa yang disurvei. Lantas dimana kesalahan survei yang dilakukan oleh Renald?
Untuk menjawab permasalahan ini, Anda perlu memahami konsep diagram venn matematika.
Mari kita lihat apa itu diagram venn, himpunan diagram venn, dan jenis-jenisnya.

Apa itu Diagram Venn?
Diagram Venn dicetuskan oleh ilmuwan asal Inggris, bernama John Venn yang menampilkan korelasi atau hubungan antar himpunan yang berkesuaian dalam suatu kelompok. Diagram Venn adalah diagram matematika yang digunakan untuk menyatakan hubungan antar dua himpunan atau lebih dalam himpunan semesta. Diagram pen ini menggambarkan hubungan antar elemen-elemen yang ada di dalam himpunan, memudahkan kita untuk memahami interaksi antara dua atau lebih kelompok data.
Himpunan sendiri merupakan kumpulan objek yang dapat didefinisikan dengan jelas dan terukur. Sebagai contoh himpunan siswa kelas 7 yang memiliki tinggi badan 120 cm. Anda dapat mengelompokkanya dengan mudah karena ada tolok ukur tinggi badan 120 cm. Tapi dapatkah Anda menyatakan himpunan aktris Indonesia yang cantik? Sulit untuk mengukur nilai cantik dalam beberapa indikator sehingga hal itu tidak dapat disebut sebagai himpunan karena tidak dapat didefinisikan dengan jelas dan terukur.
Dari sini, diagram ven bertugas untuk menggambarkan himpunan tersebut ke dalam sebuah diagram agar lebih mudah dipahami. Diagram ven dimanfaatkan untuk penyajian data secara saintifik serta teknik yang bermanfaat di bidang matematika, statsitika, serta aplikasi komputer.
Ada beberapa hal yang perlu diperhatikan dalam menggambar diagram venn, seperti:
- Himpunan semesta (S) dinyatakan dalam bentuk persegi panjang. Himpunan semesta menyatakan semua anggota himpunan yang dibicarakan.
- Himpunan lain yang menjadi fokus pembahasan dinyatakan dlaam bentuk lingkaran atau kurva tertutup.
- Anggota setiap himpunan dinyatakan dalam bentuk titik atau noktah.
- Jika anggota himpunan tak terhingga,masing-masing anggota tidak perlu dinyatakan dalam bentuk titik.
Misalkan terdapat himpunan semesta S = {a, b, c, d, e} dan himpunan lain A = {b,d,e}, maka dapat digambarkan menjadi
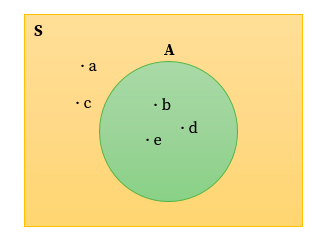
Secara matematis, A merupakan himpunan bagian dari semesta atau dapat dituliskan dalam simbol A ⊂ B
Yang perlu Anda ketahui, dalam satu himpunan semesta bisa saja memiliki lebih dari satu himpunan bagian sehingga jika digambarkan akan memiliki banyak lingkaran atau kurva tertutup.
Karakteristik Diagram Venn
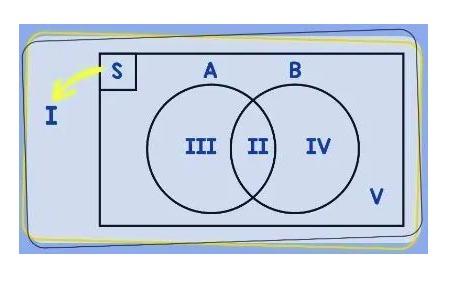
Apa yang dapat Anda ketahui dari gambar di atas?
Gambar diagram venn tersebut menjelas beberapa kata kunci utama yang perlu Anda pahami;
I. Menunjukkan himpunan semesta yang menggambarkan totoal dari anggota yang dibicarakan
II. Daerah yang merupakan milik himpunan A dan B (A ∩ B).
III. Banyak anggota himpunan A saja
IV. Banyak anggota himpunan B saja
V. Banyak anggota semesta dan bukan anggota himpunan A maupun B.
Cek di sini untuk pelatihan statistik
Macam-macam Diagram Venn
Ada beberapa macam bentuk himpunan diagram Venn yang menggambarkan hubungan antar himpunan. Berikut adalah macam-macam diagram venn yang dapat anda pelajari:
Himpunan Berpotongan
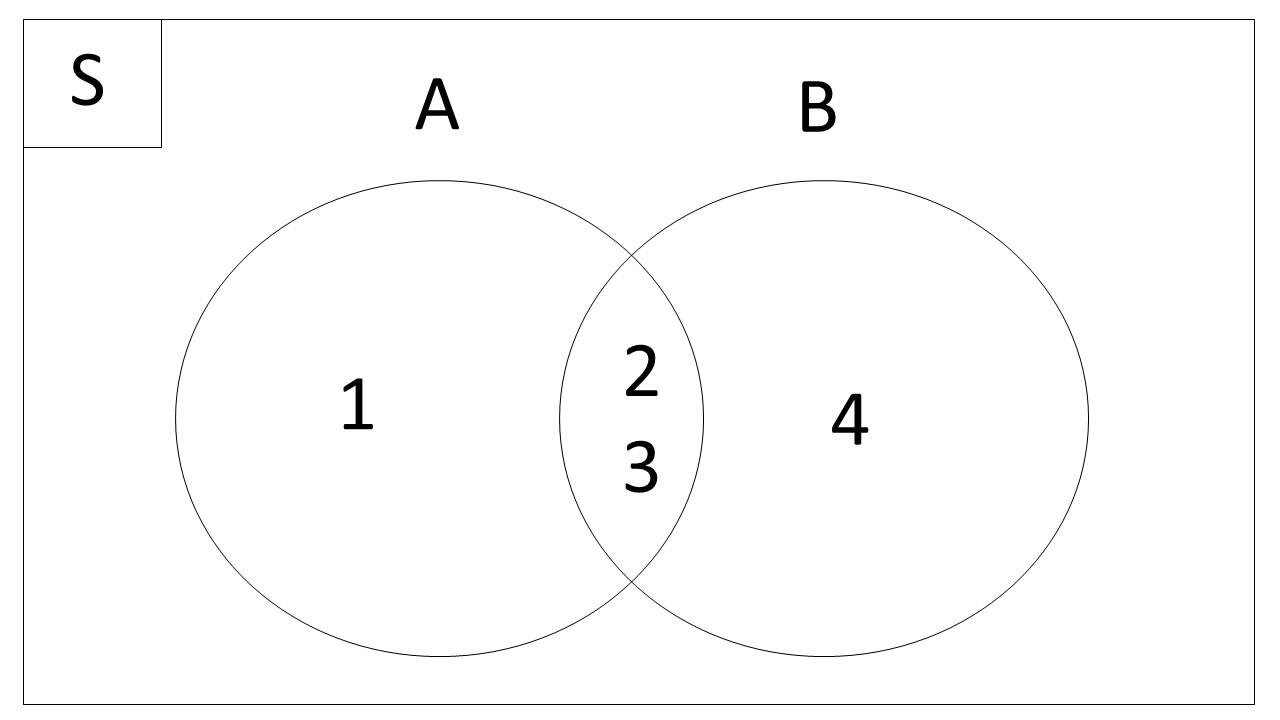
Himpunan berpotongan adalah salah satu konsep dasar dalam diagram Venn yang sering dijumpai. Himpunan A dan B dikatakan berpotongan jika ada anggota yang sama di antara kedua himpunan tersebut. Potongan ini biasanya digambarkan dengan irisan dua lingkaran. Dalam notasi, kita menuliskan irisan diagram venn ini dengan simbol A ∩ B.
Contoh:
- Himpunan A = {1, 2, 3}
- Himpunan B = {2, 3, 4}
Pada diagram Venn, angka 2 dan 3 adalah anggota bersama yang masuk ke dalam irisan A dan B. Dengan demikian, A ∩ B = {2, 3}. Gambar ini akan menunjukkan bahwa ada dua elemen yang beririsan antara himpunan A dan B.
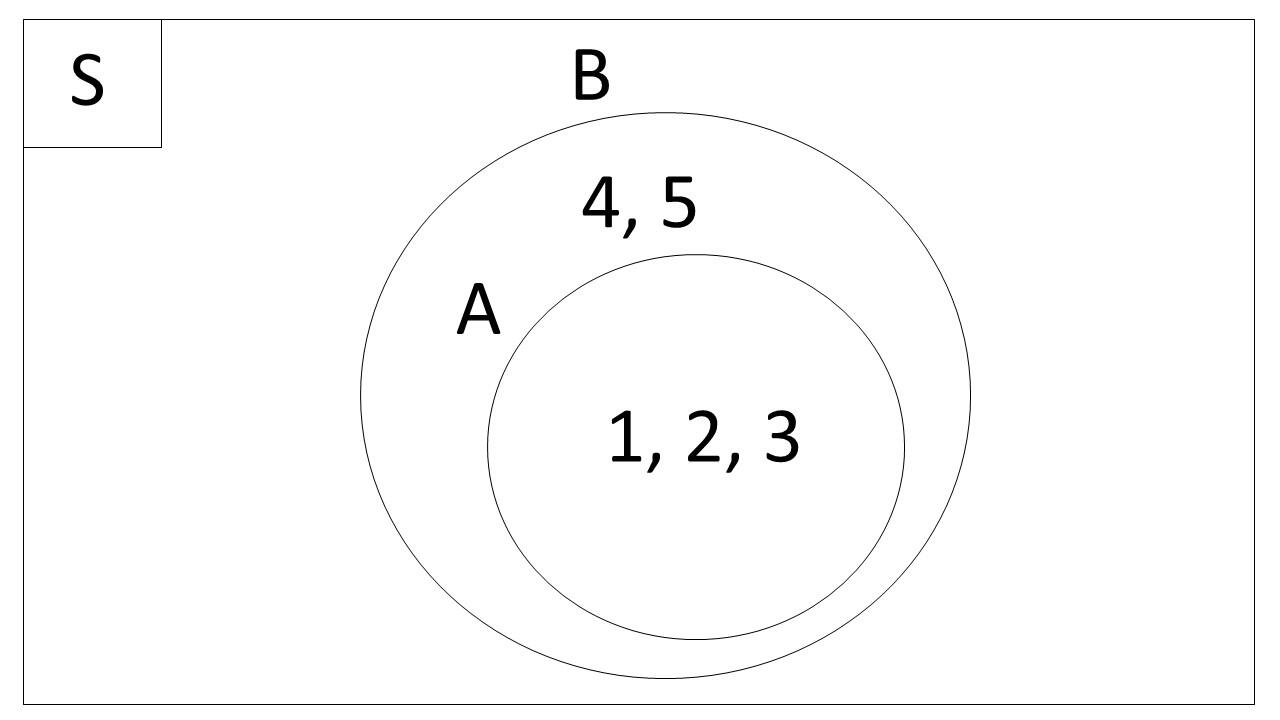
Himpunan Bagian
Himpunan bagian terjadi ketika semua anggota himpunan A adalah anggota dari himpunan B. Ini berarti himpunan A sepenuhnya ada di dalam himpunan B, tetapi sebaliknya, tidak semua elemen di B harus ada di A. Himpunan bagian ini sering digambarkan dengan satu lingkaran berada sepenuhnya di dalam lingkaran yang lain.
Contoh:
- Himpunan A = {1, 2, 3}
- Himpunan B = {1, 2, 3, 4, 5}
Pada diagram Venn, kita dapat melihat bahwa himpunan A sepenuhnya berada di dalam himpunan B, karena semua anggota A (1, 2, 3) juga ada di dalam B. Dengan demikian, kita bisa menyatakan A ⊆ B (A adalah himpunan bagian dari B).
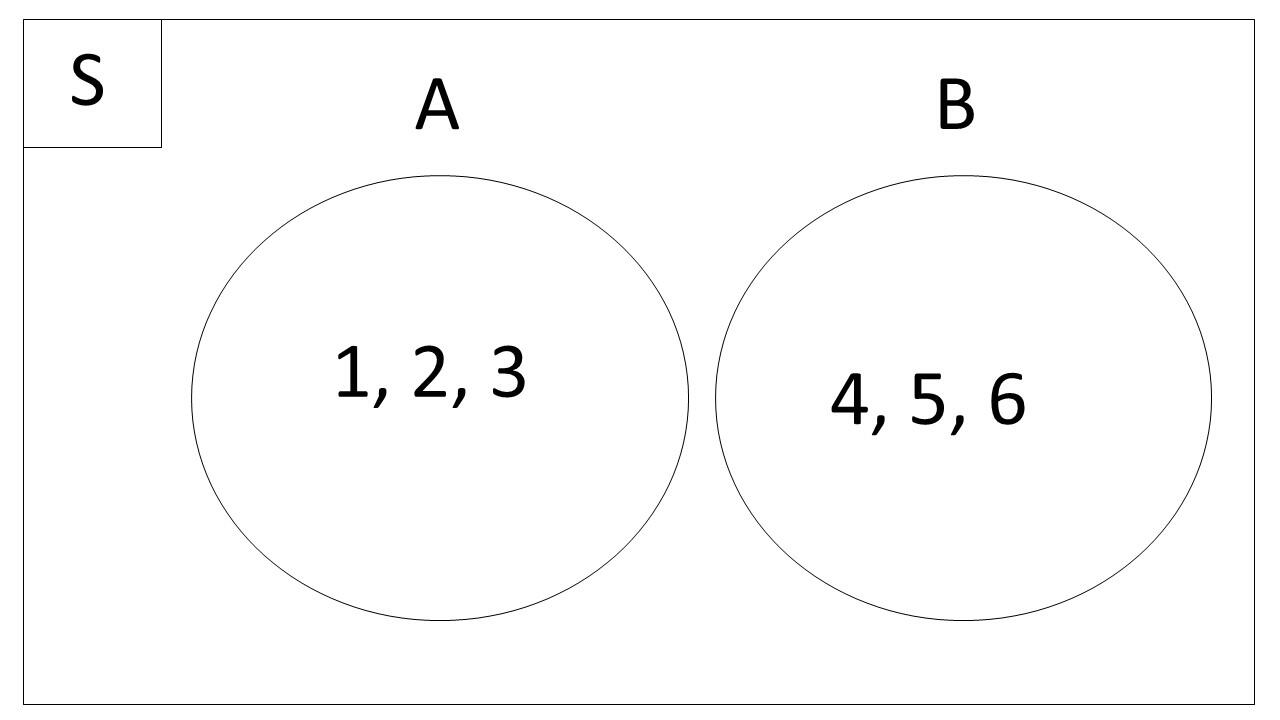
Himpunan Saling Lepas
Himpunan saling lepas terjadi ketika dua himpunan tidak memiliki anggota yang sama sama sekali. Artinya, tidak ada irisan antara kedua himpunan tersebut. Dalam diagram Venn, ini digambarkan dengan dua lingkaran yang tidak saling berpotongan. Dalam notasi, kita dapat menulisnya dengan A // B.
Contoh:
- Himpunan A = {1, 2, 3}
- Himpunan B = {4, 5, 6}
Karena tidak ada anggota yang sama antara A dan B, maka A dan B disebut himpunan yang saling lepas. Di diagram Venn, dua lingkaran ini akan digambar terpisah tanpa saling beririsan.
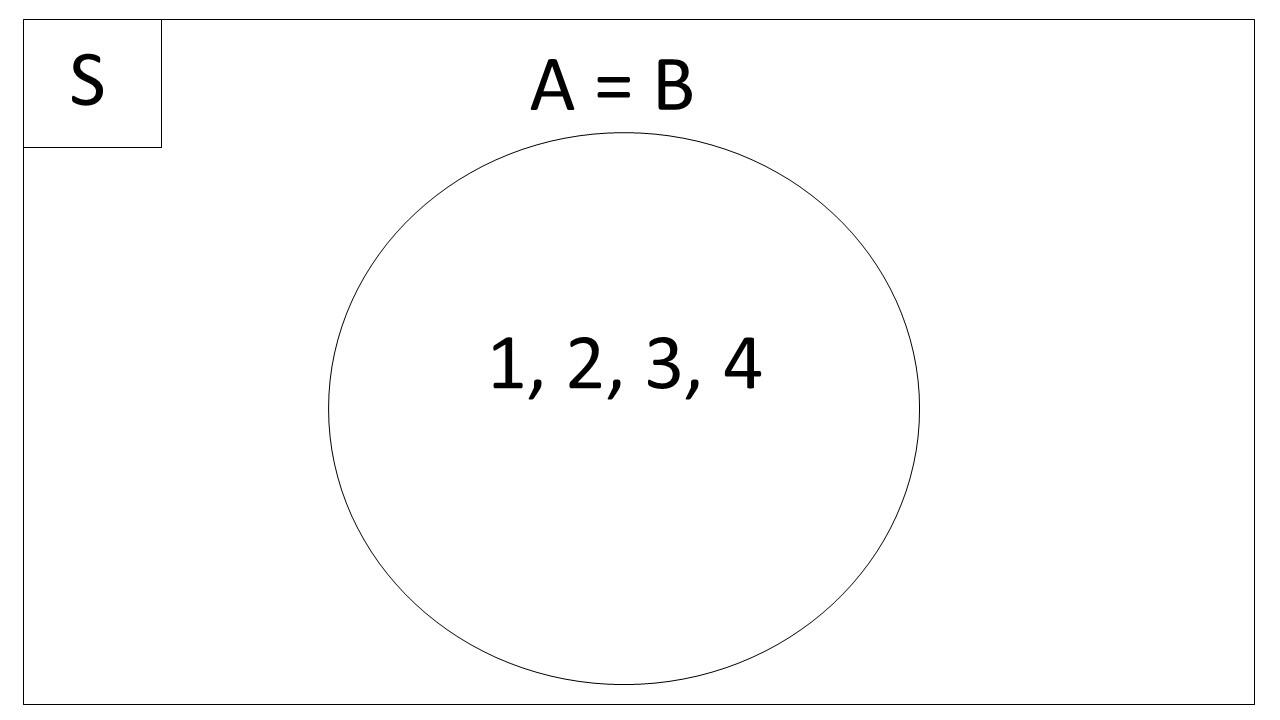
Himpunan Sama
Himpunan sama terjadi ketika semua elemen dari himpunan A juga ada di dalam himpunan B dan sebaliknya. Dalam diagram Venn, kedua himpunan akan digambarkan dengan dua lingkaran yang tumpang tindih sepenuhnya. Ini berarti kedua himpunan tersebut memiliki anggota yang identik satu sama lain.
Contoh:
- Himpunan A = {1, 2, 3, 4}
- Himpunan B = {1, 2, 3, 4}
Karena setiap elemen A juga ada di dalam B, dan setiap elemen B juga ada di dalam A, kita bisa menyatakan A = B. Dalam diagram Venn, kedua lingkaran ini akan terlihat tumpang tindih secara penuh.
Cek di sini untuk les matematika terdekat
Contoh Soal Himpunan Diagram Venn

Agar and dapat lebih paham mengenai diagram venn, mari kita lihat beberapa contoh soal diagram venn 2 himpunan berikut ini:
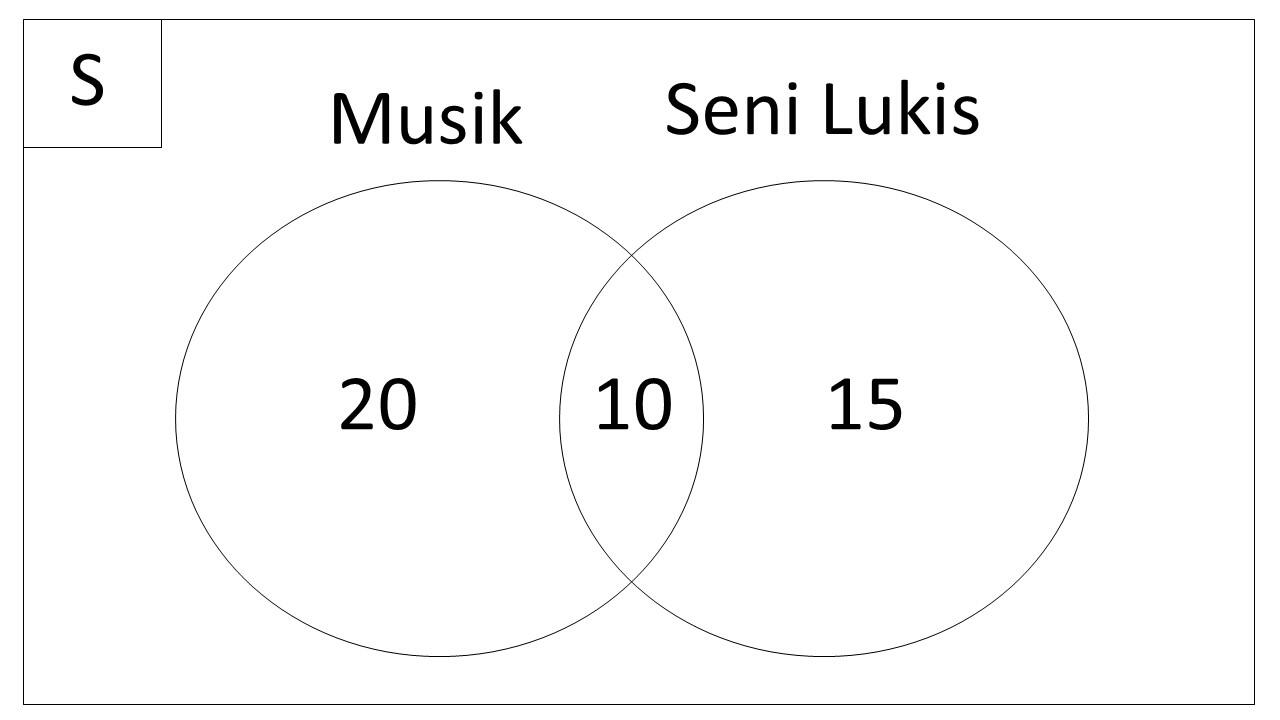
Soal Diagram Venn 1
Di sebuah sekolah, 30 siswa mengikuti Ekstrakurikuler Musik dan 25 siswa mengikuti Ekstrakurikuler Seni Lukis. Dari 25 siswa yang mengikuti Seni Lukis, 10 siswa juga mengikuti Musik. Tentukan berapa siswa yang hanya mengikuti Ekstrakurikuler Musik?
Pembahasan: Kita bisa menggunakan diagram Venn untuk menyelesaikan soal ini.
- Total siswa yang mengikuti Musik = 30
- Total siswa yang mengikuti Seni Lukis = 25
- Jumlah siswa yang mengikuti kedua ekstrakurikuler (Musik dan Seni Lukis) = 10
Cara menghitung diagram venn jumlah siswa yang hanya mengikuti Musik, kita kurangi total siswa yang mengikuti Musik dengan jumlah siswa yang mengikuti kedua ekstrakurikuler:
Jumlah siswa yang hanya mengikuti Musik = Total siswa yang mengikuti Musik - Siswa yang mengikuti kedua ekstrakurikuler
= 30 - 10
= 20 siswa
Jawaban: 20 siswa hanya mengikuti Ekstrakurikuler Musik.
Soal Diagram Venn Komplemen 2:
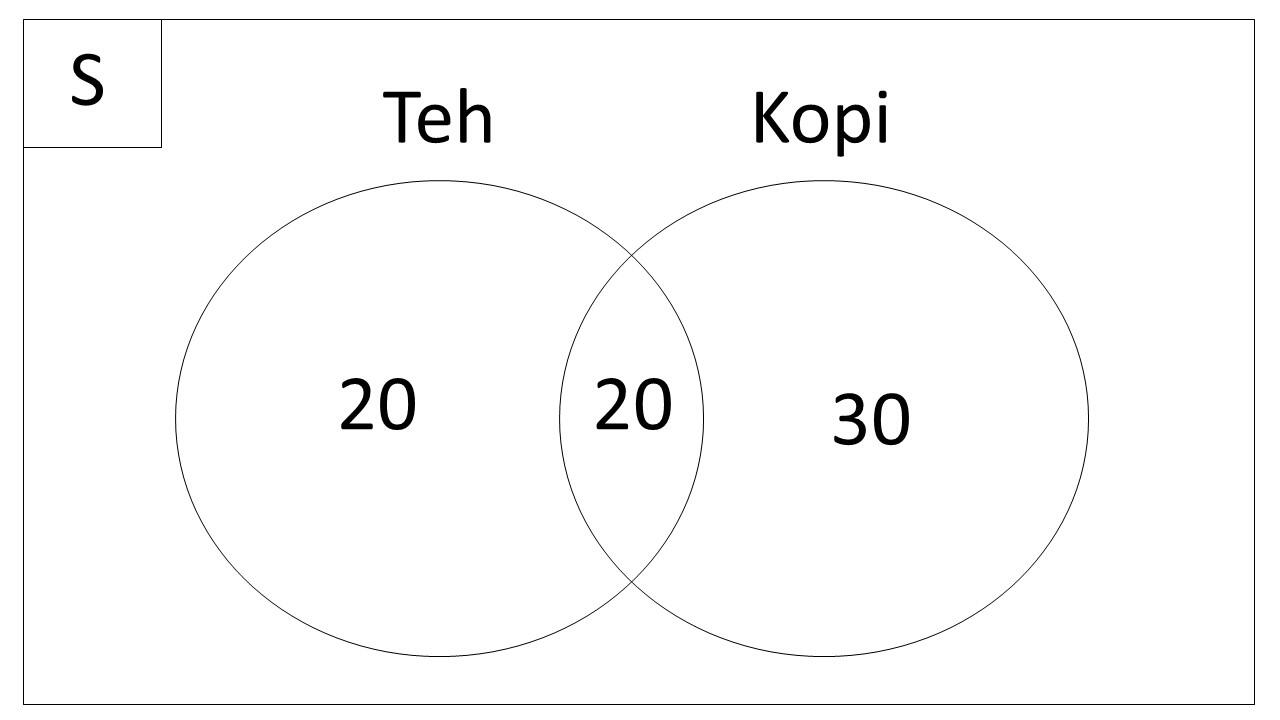
Dalam sebuah survei, 40 orang menyukai teh dan 50 orang menyukai kopi. Dari 50 orang yang menyukai kopi, 20 orang juga menyukai teh. Berapa orang yang tidak menyukai teh?
Pembahasan: Kita akan menggunakan diagram Venn untuk memecahkan masalah ini.
- Total orang yang menyukai Teh = 40
- Total orang yang menyukai Kopi = 50
- Jumlah orang yang menyukai teh dan kopi = 20
Cara menghitung diagram venn jumlah orang yang tidak menyukai teh adalah dengan cara kita kurangi total orang yang menyukai kopi dengan orang yang menyukai keduanya:
Jumlah orang yang tidak menyukai teh = Total orang yang menyukai Kopi - Orang yang menyukai teh dan kopi
= 50 - 20
= 30 orang
Jawaban: 30 orang hanya menyukai Kopi.
Soal Diagram Venn 2 Himpunan 3:
Di sebuah komunitas, 60 orang suka berenang dan 70 orang suka berlari. 30 orang suka berenang dan berlari. Tentukan berapa banyak orang yang berada dalam komunitas tersebut.
Pembahasan: Ini adalah soal yang melibatkan dua himpunan dengan perpotongan.
- Total orang yang suka Berenang = 60
- Total orang yang suka Berlari = 70
- Jumlah orang yang suka Berenang dan Berlari = 30
Untuk mencari total orang dalam komunitas ini, kita dapat menggunakan rumus untuk menghitung jumlah total orang dalam dua himpunan yang berpotongan:
Jumlah total orang = Orang yang suka berenang + Orang yang suka berlari - Orang yang suka keduanya
= 60 + 70 - 30
= 100 orang
Jawaban: Jumlah orang yang berada dalam komunitas tersebut adalah 100 orang.
Maka dari pengertian dan bentuk diagram venn yang sudah Anda pelajari. Dapatkah Anda membantu Renald menyelesaikan tugas surveinya?
Setelah memahami konsep dasar dan contoh soal tentang diagram Venn, kini saatnya untuk mendalami lebih lanjut! Diagram Venn adalah diagram matematika yang sangatlah berguna. Jika anda merasa sedang kesusahan dalam mempelajari diagram venn, jangan ragu untuk mencari les matematika di Superprof! Di sana, anda bisa menemukan banyak pengajaran berkualitas yang dapat membantu anda memahami lebih dalam tentang diagram Venn bahkan anda dapat mempelajari diagram venn 3 himpunan atau diagram venn 4 himpunan. Jadi, tunggu apa lagi? Cari guru disuperprof dan mulailah belajar sekarang juga! Bagi kamu yang berada di Bandung, pertimbangkan untuk mencari tempat les matematika di bandung guna mendukung pemahaman matematika secara mendalam.
Kami juga menyarankan Anda untuk membaca matematika dasar tentang bilangan bulat, juga bilangan pecahan dan operasi hitungnya. Itu akan sangat membantu Anda dalam menguasai ilmu matematika.
Ringkaskan dengan AI
















Sy senang dan sy suka dan terimakasih bnyk untuk membawanya Sa
sama-sama, semoga bermanfaat ya :)