
Pengertian Bentuk Rasional
Bilangan rasional adalah salah satu konsep penting dalam matematika yang diajarkan sejak di bangku sekolah. Bentuk rasional adalah bilangan yang dapat dinyatakan dalam bentuk pecahan  , di mana
, di mana 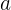 dan
dan 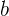 adalah bilangan bulat dan
adalah bilangan bulat dan 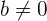 . Dalam bentuk pecahan ini,
. Dalam bentuk pecahan ini, 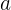 disebut pembilang dan
disebut pembilang dan 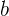 disebut penyebut.
disebut penyebut.
Bentuk rasional adalah bagian dari himpunan bilangan real, yang mencakup bilangan bulat, bilangan cacah, dan bilangan desimal berulang. Bilangan rasional dapat diubah menjadi bentuk desimal yang berhenti pada suatu titik atau membentuk pola pengulangan. Misalnya,  dapat diubah menjadi 0.5, dan
dapat diubah menjadi 0.5, dan  dapat diubah menjadi 0.333...
dapat diubah menjadi 0.333...
Mengidentifikasi bentuk rasional dari suatu bilangan adalah proses penting dalam matematika. Sebagai contoh, untuk membuktikan bahwa suatu bilangan adalah rasional, kita dapat mengubahnya ke dalam bentuk pecahan  .
.
Cek di sini untuk les privat Matematika Jakarta Timur
Contoh:
- Bilangan 0.75 adalah bilangan rasional karena dapat dinyatakan sebagai 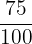 atau disederhanakan menjadi
atau disederhanakan menjadi  .
.
- Bilangan 1.25 adalah bilangan rasional karena dapat dinyatakan sebagai 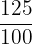 atau disederhanakan menjadi
atau disederhanakan menjadi  .
.
Sifat-Sifat Bilangan Rasional
Bilangan rasional memiliki beberapa sifat penting yang memudahkan kita dalam melakukan operasi matematika. Berikut adalah beberapa sifat tersebut:
- Tertutup terhadap penjumlahan dan perkalian: Jika
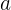 dan
dan 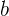 adalah bilangan rasional, maka
adalah bilangan rasional, maka 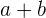 dan
dan 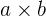 juga merupakan bilangan rasional.
juga merupakan bilangan rasional. - Asosiatif: Penjumlahan dan perkalian bilangan rasional bersifat asosiatif. Artinya,
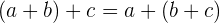 dan
dan 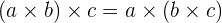 .
. - Distributif: Perkalian terhadap penjumlahan bilangan rasional bersifat distributif, yaitu
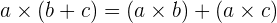 .
. - Komutatif: Penjumlahan dan perkalian bilangan rasional bersifat komutatif. Artinya,
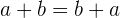 dan
dan 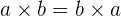 .
. - Unsur identitas: Bilangan rasional memiliki unsur identitas untuk penjumlahan (0) dan perkalian (1). Artinya,
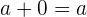 dan
dan 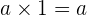 .
. - Unsur invers: Setiap bilangan rasional
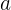 memiliki invers terhadap penjumlahan
memiliki invers terhadap penjumlahan 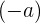 dan perkalian
dan perkalian 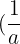 jika
jika 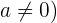 . Artinya,
. Artinya, 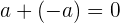 dan
dan 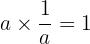 .
.
Jenis-Jenis Bilangan Rasional
Bilangan rasional dapat dibagi menjadi beberapa jenis berdasarkan bentuk dan sifatnya:
- Pecahan murni: Pecahan di mana pembilang lebih kecil dari penyebutnya, contohnya
 .
. - Pecahan campuran: Pecahan yang terdiri dari bilangan bulat dan pecahan biasa, contohnya 2
 .
. - Pecahan palsu: Pecahan di mana pembilang lebih besar atau sama dengan penyebutnya, contohnya
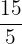 .
. - Desimal terbatas: Bilangan desimal yang berhenti pada suatu titik, contohnya 0.25.
- Desimal tak terbatas berulang: Bilangan desimal yang memiliki pola pengulangan, contohnya 0.333...

Perbedaan antara Bilangan Irasional dan Rasional
Untuk memahami perbedaan antara irasional dan rasional, kita perlu memahami definisi keduanya. Bilangan rasional, seperti yang telah dijelaskan, dapat dinyatakan dalam bentuk  di mana
di mana 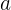 dan
dan 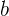 adalah bilangan bulat dan
adalah bilangan bulat dan 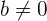 .
.
Sebaliknya, bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk pecahan  dengan
dengan 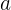 dan
dan 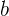 sebagai bilangan bulat. Bilangan irasional tidak dapat diubah menjadi desimal yang berhenti atau berulang. Contoh bilangan irasional termasuk √2, π, dan e. Misalnya, √2 adalah bilangan irasional karena desimalnya adalah 1.414213562..., yang tidak berhenti dan tidak berulang.
sebagai bilangan bulat. Bilangan irasional tidak dapat diubah menjadi desimal yang berhenti atau berulang. Contoh bilangan irasional termasuk √2, π, dan e. Misalnya, √2 adalah bilangan irasional karena desimalnya adalah 1.414213562..., yang tidak berhenti dan tidak berulang.
Jika sudah paham pengertian bilangan rasional, coba klik ini untuk mengetahui pengertian polinomial!
Bilangan Tidak Real
Bilangan tidak real adalah konsep yang berbeda dari bilangan rasional dan irasional. Bilangan tidak real, atau bilangan kompleks, memiliki bentuk 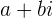 , di mana
, di mana 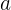 dan
dan 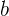 adalah bilangan real dan
adalah bilangan real dan 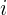 adalah satuan imajiner dengan sifat
adalah satuan imajiner dengan sifat 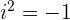 ). Contoh bilangan tidak real meliputi
). Contoh bilangan tidak real meliputi 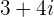 ,
, 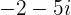 , dan
, dan 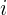 .
.
Bilangan kompleks digunakan dalam berbagai bidang matematika dan teknik, terutama dalam analisis sinyal dan pemrosesan gambar.
Tambah kemampuan matematika Anda dengan mempelajari limit fungsi Aljabar.

Apakah bilangan rasional dapat dioperasikan dalam operasi integral?
Contoh Soal Rasional dan Jawabannya
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk pecahan  , di mana
, di mana 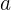 dan
dan 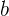 adalah bilangan bulat dan
adalah bilangan bulat dan 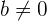 . Dalam matematika, pemahaman tentang bilangan rasional sangat penting karena mereka sering digunakan dalam berbagai operasi dan perhitungan. Berikut adalah beberapa contoh soal bilangan rasional dan penyelesaiannya yang dapat membantu memperdalam pemahaman tentang bilangan rasional.
. Dalam matematika, pemahaman tentang bilangan rasional sangat penting karena mereka sering digunakan dalam berbagai operasi dan perhitungan. Berikut adalah beberapa contoh soal bilangan rasional dan penyelesaiannya yang dapat membantu memperdalam pemahaman tentang bilangan rasional.
Contoh Soal 1: Menyatakan Bilangan dalam Bentuk Pecahan
Soal: Nyatakan bilangan 0.75 dalam bentuk pecahan.
Jawaban:
0.75 dapat dinyatakan sebagai 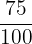 . Dengan menyederhanakan pecahan tersebut, kita mendapatkan:
. Dengan menyederhanakan pecahan tersebut, kita mendapatkan:
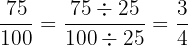
Jadi, 0.75 dalam bentuk pecahan adalah  .
.
Contoh Soal 2: Mengidentifikasi Bilangan Rasional
Soal: Tentukan apakah bilangan 0.333... adalah bilangan rasional.
Jawaban:
Bilangan 0.333... memiliki pola pengulangan, yang berarti dapat dinyatakan dalam bentuk pecahan. Kita dapat menuliskan 0.333... sebagai  . Karena
. Karena  adalah bentuk pecahan di mana pembilang dan penyebut adalah bilangan bulat dan penyebut tidak nol, maka 0.333... adalah bilangan rasional.
adalah bentuk pecahan di mana pembilang dan penyebut adalah bilangan bulat dan penyebut tidak nol, maka 0.333... adalah bilangan rasional.
Contoh Soal 3: Menyederhanakan Pecahan
Soal: Sederhanakan pecahan 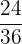 .
.
Jawaban:
Untuk menyederhanakan pecahan 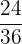 , kita mencari faktor persekutuan terbesar (FPB) dari 24 dan 36, yaitu 12. Kemudian, kita membagi pembilang dan penyebut dengan FPB tersebut:
, kita mencari faktor persekutuan terbesar (FPB) dari 24 dan 36, yaitu 12. Kemudian, kita membagi pembilang dan penyebut dengan FPB tersebut:
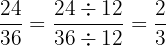
Jadi, pecahan 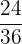 yang disederhanakan adalah
yang disederhanakan adalah  .
.
Contoh Soal 4: Penjumlahan Pecahan
Soal: Hitung hasil dari 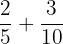 .
.
Jawaban:
Untuk menjumlahkan pecahan dengan penyebut yang berbeda, kita perlu menyamakan penyebutnya terlebih dahulu. Penyebut yang sama untuk 5 dan 10 adalah 10:
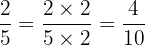
Sekarang, kita dapat menjumlahkan pecahan-pecahan tersebut:
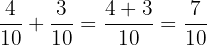
Jadi, hasil dari 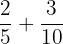 adalah
adalah 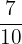 .
.
Contoh Soal 5: Pengurangan Pecahan
Soal: Hitung hasil dari 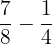 .
.
Jawaban:
Untuk mengurangkan pecahan dengan penyebut yang berbeda, kita perlu menyamakan penyebutnya terlebih dahulu. Penyebut yang sama untuk 8 dan 4 adalah 8:
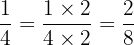
Sekarang, kita dapat mengurangkan pecahan-pecahan tersebut:
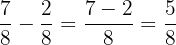
Jadi, hasil dari 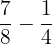 adalah
adalah  .
.
Contoh Soal 6: Perkalian Pecahan
Soal: Hitung hasil dari 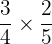 .
.
Jawaban:
Untuk mengalikan dua pecahan, kita mengalikan pembilang dengan pembilang dan penyebut dengan penyebut:
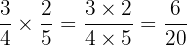
Kemudian, kita menyederhanakan pecahan tersebut:
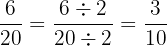
Jadi, hasil dari 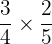 adalah
adalah 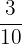 .
.
Contoh Soal 7: Pembagian Pecahan
Soal: Hitung hasil dari 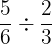 .
.
Jawaban:
Untuk membagi dua pecahan, kita mengalikan pecahan pertama dengan kebalikan dari pecahan kedua:
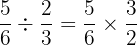
Kemudian, kita mengalikan pembilang dengan pembilang dan penyebut dengan penyebut:
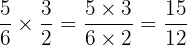
Selanjutnya, kita menyederhanakan pecahan tersebut:
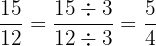
Jadi, hasil dari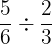 adalah
adalah  atau 1
atau 1  .
.
Contoh Soal 8: Menyatakan Bilangan Rasional dalam Bentuk Desimal
Soal: Nyatakan  dalam bentuk desimal.
dalam bentuk desimal.
Jawaban:
Untuk menyatakan pecahan dalam bentuk desimal, kita melakukan pembagian pembilang dengan penyebut:
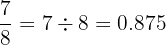
Jadi,  dalam bentuk desimal adalah 0.875.
dalam bentuk desimal adalah 0.875.
Contoh Soal 9: Menemukan Bilangan Rasional yang Terletak di Antara Dua Bilangan
Soal: Tentukan bilangan rasional yang terletak tepat di tengah-tengah antara  dan
dan  .
.
Jawaban:
Untuk menemukan bilangan rasional yang terletak di tengah-tengah antara dua bilangan rasional, kita menjumlahkan kedua bilangan tersebut dan membaginya dengan 2:
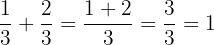
Sekarang, kita bagi hasil tersebut dengan 2:
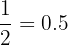
Jadi, bilangan rasional yang terletak di tengah-tengah antara  dan
dan  adalah 0.5.
adalah 0.5.
Contoh Soal 10: Menyatakan Persamaan Rasional dalam Bentuk Sederhana
Soal: Sederhanakan persamaan rasional berikut: 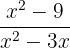 .
.
Jawaban:
Langkah pertama adalah memfaktorkan pembilang dan penyebut:
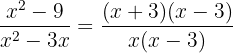
Kemudian, kita menyederhanakan dengan menghilangkan faktor yang sama di pembilang dan penyebut:
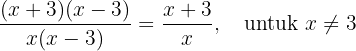
Jadi, bentuk sederhana dari 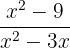 adalah
adalah 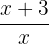 .
.
rasional.
Ikuti tulisan Kami lainnya untuk memahami konsep deret dan barisan!
Cari Les Privat Matematika? Kunjungi Website Superprof Sekarang!
Apakah Anda sedang mencari cara efektif untuk memahami materi matematika dengan lebih baik? Ingin mendapatkan bimbingan dari guru matematika yang berpengalaman? Jangan khawatir, Superprof hadir untuk membantu Anda!
Superprof adalah platform terbaik yang menawarkan guru privat matematika yang profesional dan berkompeten. Dengan les matematika di Superprof, Anda akan mendapatkan pembelajaran yang disesuaikan dengan kebutuhan dan tingkat pemahaman Anda. Guru-guru kami siap memberikan metode pengajaran yang interaktif dan menyenangkan sehingga belajar matematika menjadi lebih mudah dan menyenangkan.
Mengapa memilih Superprof?
- Guru matematika berpengalaman dan teruji
- Metode pengajaran yang disesuaikan dengan kebutuhan Anda
- Jadwal fleksibel dan lokasi yang dapat disesuaikan
- Biaya yang terjangkau dengan kualitas pengajaran terbaik
Jangan lewatkan kesempatan ini untuk meningkatkan pemahaman Anda dalam matematika. Kunjungi website Superprof sekarang dan temukan guru privat matematika yang tepat untuk Anda! Bersama Superprof, belajar matematika jadi lebih mudah dan menyenangkan.
Mulailah perjalanan belajar Anda dengan Superprof dan lihatlah perubahan signifikan dalam kemampuan matematika Anda!
Ringkaskan dengan AI
















